Главная | Обратная связь

Приклади розв’язування типових задач

Задача 2.1. У грошо-речовій лотереї на кожну 1000 квитків випадає 25 грошових і 15 речових виграшів. Куплено два квитка. Яка ймовірність, що випаде: 1) на перший квиток грошовий виграш, а на другий – речовий виграш; 2) хоча б на один квиток виграш?

Розв’язання. 1) Позначимо через Р(А) ймовірність грошового виграшу на перший квиток, Р(В/А) – ймовірність речового виграшу на другий квиток. Тоді ймовірність виграти гроші на перший квиток і якусь річ на другий буде Р(АВ)=Р(А) Р(В/А).

За класичним означенням ймовірності

Р(А)= 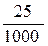, Р(В/А)= 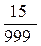. Тоді Р(АВ)=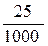 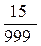»0,000375.

2) Позначимо через С виграш на перший квиток, а через D – на другий квиток. Тоді ймовірність хоча б на одного виграшу на два квитка буде Р(С+D)=Р(С)+Р(D)-Р(СD).

За класичним означенням ймовірності Р(С)=Р(D)=40/1000, тоді Р(D/С)=39/999. За теоремою добутку ймовірностей Р(СD)=Р(С)Р(D/С)=40/1000 39/999»0,00156. Отже, Р(С+D)=40/1000+40/1000–0,00156»0,07844.

Відповідь:1) »0,000375; 2) 0,07844.

Задача 2.2.Три стрільці незалежно один від одного стріляють по цілі. Ймовірність влучення в ціль для першого стрільця дорівнює 0,75, для другого – 0,8, для третього – 0,9. Визначити ймовірність того, що а) всі три стрільці одночасно влучать в ціль; б) в ціль влучить хоча б один стрілок.

Розв’язання. а) Позначимо через Р(А) ймовірність влучення в ціль для першого стрільця, через Р(В) – для другого стрільця, через Р(С) – для третього стрільця. За умовою Р(А)=0,75, Р(В)=0,8, Р(С)=0,9.

За теоремою добутку ймовірностей три стрільця одночасно влучать в ціль з ймовірністю

Р(АВС)= Р(А)∙Р(В)∙Р(С)=0,75∙0,8∙0,9=0,54.

б)Ймовірність промаху першого стрільця Р(Ā)=1–0,75=0,25, для другого стрільця – Р( 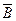)=1–0,8=0,2, для третього – Р( )=1–0,9=0,1, тоді ймовірність промаху всіх стрільців одночасно

Р( 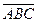)=Р(Ā)∙Р( 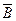)∙Р( )=0,25∙0,2∙0,1=0,005.

Подія, що заключається у влучанні в ціль хоча б одного стрільця, протилежна події Р( 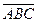), тому Р=1–Р( 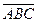)=1–0,005=0,995.

Відповідь: а) 0,54; б)0,995.

 

Індивідуальні завдання для самостійної роботи

1. Літак може потерпіти аварію, якщо буде відмова або конструкції планера, або двигунної системи, або системи керування. Двигунна система складається з трьох двигунів. Відомо, що ймовірність відмови конструкції 0,001, двигуна 0,01, системи керування 0,005. Знайти ймовірність безаварійного польоту, якщо відмови – події незалежні.

2. За деякий проміжок часу амеба може загинути з ймовірністю 1/4, вижити з ймовірністю 1/4 і поділитися на дві з ймовірністю 1/2. в наступний такий же проміжок часу з кожною амебою незалежно від її “походження” відбувається теж саме. Скільки амеб і з якими ймовірностями може існувати на кінець другого проміжку часу?

3. З колоди в 36 карт навмання одна за одною витягують дві карти. Знайти ймовірність того, що: а) витягнуті дві карти бубнової масті; в) витягнуті король і дама.

4. З корзини, що містить 3 білих і 7 червоних кульок, навмання послідовно і без повернень витягують дві кульки. Події: А={перша кулька біла}, В={друга кулька біла}, С={хоча б одна з витягнутих кульок біла}. Обчислити ймовірності Р(В/А), Р(А/В) і Р(А/С).

5. У середньому один ящик зі 100 містить у собі нестандартну деталь. Яка ймовірність того, що 4 взяті навмання ящики містять тільки стандартні деталі?

6. Достатньою умовою здачі колоквіуму є відповідь на два з трьох заданих питань. Студент не знає сім питань із тих сорока п’яти, що пропонуються. Яка ймовірність здачі колоквіуму?

7. Два мисливці стріляють по одній качці, кожен робить по одному пострілу. Ймовірність влучання для першого і другого мисливця відповідно рівна 0,75 та 0,9. Яка ймовірність влучання хоча б при одному пострілі? Як зміниться результат, якщо мисливці зроблять по 2 постріли?

8. Кинуто 3 гральні кубики. Знайти ймовірності наступних подій: а) на двох гранях, що випали, буде 3 вічка, на третій – інше число вічок; б) на двох гранях, що випали, буде однакове число вічок, а на третій – інше; в) на всіх гранях випаде різне число вічок.

9. Для сигналізації встановлено 3 пристрої з ймовірністю спрацювання 0.65, 0.8 і 0.95. Знайти ймовірність того, що: а) спрацює хоча б один пристрій; б) один пристрій; в) три пристрої.

10. З колоди в 36 карт навмання одна за одною витягують чотири карти. Знайти ймовірність того, що: а) витягнуті 4 карти масті треф; в) витягнуті 3 валета і дама.

11. Ймовірність того, що стрілок при одному пострілі влучить в мішень, дорівнює р=0,9. Стрілок зробив три постріли. Знайти ймовірність того, що всі три постріли влучні.

12. У двох ящиках знаходяться деталі: у першому – 10 (з них 3 стандартних, у другому 15 (з них 6 стандартних). З кожного ящика навмання виймають по одній деталі. Знайти ймовірність того, що обидві деталі виявляться стандартними.

13. У студії телебачення 3 телевізійних камери. Для кожної камери ймовірність того, що вона включена в даний момент, дорівнює р=0,6. Знайти ймовірність того, що в даний момент включена хоча б одна камера.

14. Підприємство виготовляє 95% виробів стандартних. причому з них 86 % – першого сорту. Знайти ймовірність того, що взятий навмання виріб, виготовлений цим підприємством, виявиться першого сорту.

15. З цифр 1, 2, 3, 4, 5 спочатку вибирається одна, а потім з чотирьох, що залишилися, – друга цифра. Вважається, що всі 20 випадків рівноможливі. Знайти ймовірність того, що буде обрана непарна цифра: а) першого разу; б) за другим разом; в) обидва рази.

16. Ймовірність того, що при одному пострілі стрілок влучає в десятку, дорівнює 0,6. Скільки пострілів повинен зробити стрілок, щоб з ймовірністю не менше 0,8 він влучив у десятку хоча б один раз?

17. Три електричні лампочки послідовно включені в електричне коло. Ймовірність того, що одна (будь-яка) лампочка перегорить, якщо напруга в мережі перевищує номінальну, дорівнює 0,6. Знайти ймовірність того, що при підвищеній напрузі струму в колі не буде.

18. Ймовірності влучення в ціль при стрільбі першої і другої гармати відповідно дорівнюють: р₁=0,7, р₂=0,8. Знайти ймовірність влучання при одному залпі (з обох гармат) хоча б однією з гармат.

19. У грошо-речовій лотереї на кожні 10000 квитків випадає 50 грошових і 150 речових виграшів. Чому рівна ймовірність виграшу (не має значення грошового чи речового) для володаря одного лотерейного квитка?

20. Кинуто 3 гральні кубики. Знайти ймовірності наступних подій: а) на одній з граней випаде 5 вічок; б) на всіх гранях випаде однакове число вічок.

21. З колоди в 36 карт навмання одна за одною витягують дві карти. Знайти ймовірність того, що: а) витягнуті два короля; б) витягнуті дві карти червової масті.

22. 2% учнів школи – невстигаючі. Серед встигаючих учнів 54% вчаться добре і відмінно. Яка ймовірність того, що навмання обраний учень вчиться добре або відмінно?

23. У першому ящику 5 білих кульки, 13 червоних і 9 чорних, в другому – 11 білих, 7 червоних і 3 чорних. Навмання беруть по одній кульці з кожного ящика. Яка ймовірність того, що вони одного кольору?

24. Турист може поїхати до центрального парку міста або автобусом, який ходить через кожні 10 хв, або тролейбусом, який ходить через кожні 30 хв. Яка ймовірність того, що турист, який підійшов до зупинки, поїде протягом наступних п’яти хвилин?

25. У корзині міститься 6 білих і 4 синіх кульок. Хлопчик навмання послідовно і без повернень витягує дві кульки. Подія: А={перша кулька синя}, B={друга кулька синя}, C={хоча б одна з витягнутих кульок синя}. Обчислити ймовірності Р(В/А), Р(А/В) і Р(А/С).

26. Ймовірність того, що прилад не вийде з ладу за 5 хвилин дорівнює 0.8, а ймовірність того, що він не вийде з ладу через 8 хвилин, дорівнює 0.6. Знайти ймовірність того, що прилад, який не зіпсувався за 5 хвилин, не зіпсується і через 8 хвилин.

27. Ймовірність влучити в літак дорівнює 0.5, а ймовірність його збити дорівнює 0.1. Знайти ймовірність того, що при влученні в літак його буде збито.

28. В майстерні є три верстати. За зміну з ладу може вийти не більше одного верстата. Перший виходить з ладу з ймовірністю 0.25, другий – з ймовірністю 0.3, третій – з ймовірністю 0.15. Знайти ймовірність того, що за зміну а) жоден верстат не вийде з ладу; б) один верстат вийде з ладу.

29. З корзини, що містить 7 білих і 3 зелених кульок, навмання послідовно і без повернень витягують дві кульки. Події: А={перша кулька біла}, В={друга кулька біла}, С={хоча б одна з витягнутих кульок біла}. Обчислити ймовірності Р(В/А), Р(А/В) і Р(А/С).

30. Із корзини, що містить m білих та n чорних кульок, виймають по одній кульці і кладуть назад. Обчислити ймовірність того, що біла кулька з’явиться після k-кратного виймання чорної кульки.