 |
|
Тема: Повторні незалежні випробування. Схема і формула Бернуллі. Найбільш імовірне число “успіхів”. Граничні теореми для схеми Бернуллі
ПЛАН
І. Актуалізація опорних знань.
1. Які випробування називають незалежними?
2. Які події називаються складними, простими? Наведіть приклади.
3. Виведення й зміст формули Бернуллі.
4. Які задачі розв’язуються за допомогою теореми Пуассона?
5. В яких випадках доцільно застосовувати локальну теорему Лапласа?
6. Інтегральна теорема Лапласа.
7. Необхідність і зміст граничних теорем.
ІІ. Розв’язування вправ (непарні задачі).
6.1. Ймовірність події в кожному з однакових і незалежних дослідів дорівнює р. Знайти ймовірність того, що в п дослідах подія настане k разів:
а) р=0.2, п=7, k=5;
б) р=0.3, п=10, k=7.
6.2. У середньому 60% виробів підприємства – продукція вищої якості. Яка ймовірність того, що серед 7 виробів 4 – вищої якості?
Відповідь: »0.29.
6.3. У суді 7 присяжних. Кожен з них в одному з трьох випадків виносить несправедливий вирок. Яка ймовірність того, що на суді буде винесено справедливий вирок?
Відповідь: »0.8267.
6.4. Монета підкидається 5 разів. Яка ймовірність того, що гербів випаде більше ніж цифр?
Відповідь: 0.5.
6.5. Зростання насіння складає 70%. Яка ймовірність того, що з 10 насінин зійде: а) вісім; б) не менше восьми.
Відповідь: а) »0.2335; б) »0.3828.
6.6. На фабриці, що виготовляє олівці, брак складає 3%. Яка ймовірність того, що при покупці 5 олівців принаймні 2 будуть якісними?
Відповідь: 0.9985.
6.7. У сім'ї п'ять дітей. Знайти ймовірність того, що серед цих дітей: а) три хлопчика; б) не більше двох хлопчиків; в) більше двох хлопчиків; г) не менше двох і не більше трьох хлопчиків. Ймовірність народження хлопчика прийняти рівній 0,51.
Відповідь: а) 0.32, б) 0.48, в) 0.52, г) 0.62.
6.8. Відомо, що ймовірність народження хлопчика дорівнює 0,515. Яка ймовірність того, що в сім’ї з трьох дітей не менше двох дівчаток?
Відповідь: 0.2078.
6.9. Два рівносильних шахіста грають в шахи. Що ймовірніше: виграти дві партії з чотирьох чи три партії з шести (нічию до уваги не брати)?
Відповідь: ймовірніше виграти дві партії з чотирьох.
6.10. Два рівносильних шахіста грають в шахи. Що ймовірніше виграти: три партії з шести чи чотири з восьми (нічию до уваги не брати)?
Відповідь: ймовірніше виграти три партії з шести.
6.11. У результаті багаторічних спостережень встановлено, що ймовірність випадання дощу 1 липня в м. Кіровограді дорівнює 4/17. Визначити найімовірніше число дощових днів 1 липня в м. Кіровограді за найближчі 50 років.
Відповідь: 11;12.
6.12. Ймовірність влучення в мішень при одному пострілі становить 0.95. Знайти найімовірніше число влучень при 150 пострілах.
Відповідь: 142.
6.13. Пристрій складається з трьох незалежно працюючих основних елементів. Пристрій відмовляє, якщо відмовить хоча б один елемент. Ймовірність відмови кожного елемента за час t рівна 0,1. Знайти ймовірність безвідмовної роботи пристрою за час t, якщо: а) працюють тільки основні елементи; б) включений один резервний елемент; в) включені два резервні елементи. Вважають, що резервні елементи працюють у тому ж режимі, що й основні, ймовірність відмови кожного резервного елемента також рівна 0,1 і пристрій відмовляє, якщо працює менше трьох елементів.
Відповідь: а) 0.729, б) 0.95, в) 0.99.
6.14. Автопідприємство має 12 машин. Ймовірність виходу на лінію кожної з них дорівнює 0,8. Визначити ймовірність нормальної роботи автопідприємства, якщо для цього необхідно мати на лінії не менше 8 машин.
6.15. В ящику 10 деталей. Скільки потрібно ящиків, щоб ймовірність хоча б однієї бракованої деталі була не менше 0,8, якщо ймовірність браку дорівнює 0,01?
6.16. Ймовірність того, що при випробуванні пристрій відмовить, рівна 0,2. Скільки пристроїв треба випробувати, щоб з ймовірністю не меншою 0,9 відмовило не менше трьох пристроїв?
6.17. Стрілок стріляє в ціль до першого влучення. Знайти ймовірність того, що у стрільця залишиться хоча б один не використаний набій, якщо він отримав десять набоїв і ймовірність попадання в ціль при кожному пострілі постійна і рівна 0,2.
6.18. Квадрат зі стороною а розділений на два прямокутники, сторони яких рівні відповідно а, а/3 і а, 2а/3. На цей квадрат кидають 6 точок. Яка ймовірність того, що в великий прямокутник попало 3 точки?
7.1. Знайти ймовірність того, що подія А відбудеться рівно 70 разів у 243 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні рівна 0,25.
Відповідь: 0.0231.
7.2. Знайти ймовірність того, що подія Авідбудеться 1400 разів у 2400 випробуваннях, якщо ймовірність появи цієї події в кожному випробуванні рівна 0,6.
Відповідь: 0.0041.
7.3. Ймовірність поразки мішені при одному пострілі рівна 0,8. Знайти ймовірність того, що при 100 пострілах стрілок поразить мішень рівно 75 разів.
Відповідь: 0.04565.
7.4. Ймовірність народження хлопчика рівна 0,51. Знайти ймовірність того, що серед 100 новонароджених виявиться 50 хлопчиків.
Відповідь: 0.0782.
7.5. Ймовірність появи події в кожному з 100 незалежних випробуваннях постійна і рівна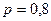 
. Знайти ймовірність того, що подія з’явиться: а) не менше 75 разів і не більше 90 разів; б) не менше 75 разів; в) не більше 74 разів.
Відповідь: а) 0.8882, б) 0.8944, в) 0.1056.
7.6. Ймовірність появи події в кожному з 2100 незалежних випробувань рівна 0,7. Знайти ймовірність того, що подія з'явиться: а) не менше 1470 і не більше 1500 разів; б) не менше 1470 разів; в) не більше 1469 разів.
Відповідь: а) 0.4236, б) 0.5, в) 0.5.
7.7. Ймовірність появи події в кожному з 21 незалежних випробувань рівна 0,7. Знайти ймовірність того, що подія з'явиться у більшості випробувань.
Відповідь: 0.95945.
7.8. Ймовірність появи подіїв кожному з незалежних випробувань рівна 0,8. Скільки потрібно провести випробувань, щоб з ймовірністю 0,9 можна було очікувати, що подія з’явиться не менше 75 разів?
Відповідь: 100.
7.9. Ймовірність появи позитивного результату в кожному з n дослідів рівна 0,9. Скільки потрібно провести дослідів, щоб з ймовірністю 0,98 можна було чекати, що не менше 150 дослідів дадуть позитивний результат?
Відповідь: 177.
7.10. Автоматична телефонна станція отримує в середньому за годину 300 викликів. Яка ймовірність того, що за дану хвилину вона отримає точно два виклики?
Відповідь: »0.29.
7.11. Книга в 1000 сторінок має 100 опечаток. Яка ймовірність того, що на випадково обраній сторінці не менше чотирьох опечаток?
Відповідь: 0.000004.
7.12. Серед насіння жита є 0.4% насінин бур’янів. Яка ймовірність при випадковому відборі 500 насінин знайти 5 насінин бур’янів?
Відповідь: 0.000055.
7.13. Ймовірність того, що електрична лампочка залишиться справною після 1000 годин роботи, дорівнює 0.2. Знайти ймовірність того, що хоча б одна з трьох ламп залишиться справною після 1000 годин роботи.
Відповідь: 0.488.
7.14. По дорозі проїжджає за добу в середньому 1000 автомобілів. Яка ймовірність того, що кількість автомобілів, які проїхали, більше 300 і менше 400? Ймовірність зустрічі автомобіля 0,4.
7.15. Знайти ймовірність того, що при 400 випробуваннях подія відбудеться 100 разів, якщо ймовірність її появи в кожному випробуванні рівна 0,01.
7.16. З партії деталей, серед яких 40% першосортних, роблять збірку агрегату. Знайти ймовірність того, що при збірці з 100 деталей 37 першосортних.
7.17. З 1000 деталей вибрали 50. Яка ймовірність того, що у вибірці 2 дефектні деталі, якщо у всій партії їх 4?
7.18. У середньому 2% виготовлених пристроїв потребують додаткового регулювання. Перевіряється 300 приладів. Яка ймовірність того, що 10 з них потребують регулювання?
7.19. Апаратура складається з 2000 деталей, ймовірність відмови кожної з яких 0,0005. Яка ймовірність того, що апаратура вийде з ладу, якщо це трапляється при відмові хоча б однієї деталі?
7.20. Ймовірність виграшу на кожен з лотерейних квитків рівна 0,02. Розрахувати ймовірність хоча б одного виграшу на n квитків для п=10, 90, 100.
7.21. На складі знаходиться продукція трьох фабрик, причому виробів першої фабрики на складі 30%, другої – 32 і третьої – 38%. Вироби першого сорту складають: для першої фабрики – 60%, для другої – 25%, для третьої – 50%. Визначити ймовірність того, що серед 300 наймання вибраних виробів першосортних не менше 130 і не більше 170.
7.22. Радіотелеграфна станція приймає цифровий текст. У силу наявності перешкод ймовірність помилкового прийому будь-якої цифри не змінюється протягом всього прийому і рівна 0,01. Вважаючи прийоми окремих цифр незалежними подіями, знайти: а) ймовірність того, що число невірно прийнятих цифр буде менше 20 в тексті з 1100 цифр; б) ймовірність того, що в тексті 7 помилок.
7.23. Якщо в середньому лівші складають 1%, які шанси на те, що серед 200 чоловік знайдеться четверо лівшів?
7.24. Ймовірність випуску свердла підвищеної хрупкості рівна 0,02. Свердла вкладаються в коробки по 100 штук. Знайти ймовірність того, що: а) у коробці не знайдеться бракованих свердел; б) бракованих свердел знайдеться не більше 3.
7.25. По каналу зв’язку передається 1000 знаків. Кожен знак може бути пошкоджений незалежно від інших з ймовірністю 0,005. Знайти наближене значення ймовірності того, що буде пошкоджено не більше трьох знаків.
ІІІ. Домашнє завдання (парні задачі).
Практичне заняття №8
Тема: Дискретна випадкова величина. Закон розподілу ймовірностей. Числові характеристики дискретних випадкових величин
ПЛАН
І. Актуалізація опорних знань.
1. Дайте означення випадкової величини. Яка випадкова величина називається дискретною?
2. Яким чином можна задати закон розподілу дискретної випадкової величини?
3. Математичне сподівання та його властивості. Фізичний зміст математичного сподівання.
4. Дисперсія та її властивості. Середнє квадратичне відхилення.
5. Моменти, асиметрія і ексцес дискретної випадкової величини.
ІІ. Розв’язування вправ (непарні задачі).
8.1. Дано ймовірності значень випадкової величини Х: значення 6 має ймовірність 0.35, значення 2 – ймовірність 0.45, значення 8 – ймовірність 0.15, значення 4 – ймовірність 0.05. Побудуйте ряд та многокутник розподілу випадкової величини Х. Знайдіть її математичне сподівання М(Х) та дисперсію D(X).
8.2. Дано ймовірності значень випадкової величини Х: значення 10 має ймовірність 0.3, значення 2 – ймовірність 0.4, значення 8 – ймовірність 0.1, значення 4 – ймовірність 0.2. Побудуйте ряд та многокутник розподілу випадкової величини Х. Знайдіть її математичне сподівання М(Х) та дисперсію D(X).
8.3. Розподіл дискретної випадкової величини задано таблицею:
| ξ | |||||
| Р | 0.2 | 0.3 | 0.35 | 0.1 | 0.05 |
Знайдіть функцію розподілу ймовірності цієї випадкової величини, математичне сподівання Мξ і Р{20<ξ≤40}.
8.4. Розподіл дискретної випадкової величини задано таблицею:
| ξ | 5.1 | 5.3 | 5.5 | 5.7 | 5.9 |
| Р | 0.2 | 0.3 | 0.1 | 0.1 | 0.3 |
Знайдіть функцію розподілу ймовірності цієї випадкової величини, математичне сподівання Мξ і Р{1.3<ξ≤1.7}.
8.5. Знайдіть закон розподілу дискретної випадкової величини Х, яка приймає тільки два значення х1 і х2, причому х1<х2, і відомі ймовірність р1=0.6 можливого значення х1, математичне сподівання М(Х)=1.4 та дисперсія D(X)=0.24
8.6. Знайдіть закон розподілу дискретної випадкової величини Х, яка приймає тільки два значення х1 і х2, причому х1<х2, і відомі ймовірність р1=0.7 можливого значення х1, математичне сподівання М(Х)=3.3 та дисперсія D(X)=0.21
8.7. Знайдіть закон розподілу дискретної випадкової величини Х, яка приймає тільки два значення х1 і х2, причому х1<х2, і відомі ймовірність р1=0.2 можливого значення х1, математичне сподівання М(Х)=2.6 та середнє квадратичне відхилення σ(X)=0.8.
8.8. Знайдіть закон розподілу дискретної випадкової величини Х, яка приймає тільки два значення х1 і х2, причому х1<х2, і відомі ймовірність р1=0.3 можливого значення х1, математичне сподівання М(Х)=3.7 та дисперсія D(X)=0.21.
8.9. Тричі стріляють по мішені. Ймовірність влучення приблизно 0.4. Нехай x – число влучень. Знайдіть Dx.
8.10. З усієї продукції, що випускає завод, 95% складають стандартні деталі. Навмання відібрано 6 деталей. Нехай x – число стандартних деталей з шести відібраних. Знайдіть Dx.
8.11. У корзині є чотири кулі з номерами від 1 до 4. Вийняли дві кулі. Нехай x – сума номерів куль. Побудуйте ряд розподілу випадкової величини x.
8.12. Тричі стріляють по мішені. Ймовірність влучення в мішень при кожному пострілі дорівнює 0.3. Нехай x – число влучень. Побудуйте ряд розподілу x.
8.13. Пристрій складається з трьох незалежно працюючих елементів. Ймовірність відмови кожного елемента в одному досліді рівна 0.1. Побудуйте закон розподілу числа елементів, що відмовили в одному досліді.
8.14. У партії з10 деталей є 8 стандартних. Навмання відібрано дві деталі. Побудуйте закон розподілу числа стандартних деталей серед відібраних.
У задачах 8.15.-8.20. випадкова величина розподілена ξ за законом:
| ξ | –2 | –1 | |||
| Р | 0.2 | 0.1 | 0.3 | 0.3 | 0.1 |
8.15. Обчисліть Мξ.
8.16. Побудуйте закон розподілу випадкової величини 3ξ–1 і знайдіть
М(3ξ–1). Порівняйте отриманий результат з 3Мξ–1.
8.17. Побудуйте закон розподілу випадкової величини 2ξ+3. Обчисліть М(2ξ+3). Порівняйте отриманий результат з 2Мξ+3.
8.18. Побудуйте закон розподілу випадкової величини ξ2 і обчисліть М(ξ2).
8.19. Побудуйте закон розподілу випадкової величини ξ2+1 і обчисліть М(ξ2+1).
8.20. Побудуйте закон розподілу випадкової величини ξ2–5 і обчисліть М(ξ2–5).
8.21. Закон розподілу дискретної випадкової величини Х задано таблицею:
| Х | ||||||||
| Р | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 |
а величини У таблицею:
| У | ||||||||
| Р | 1/4 | 1/8 | 1/16 | 1/16 | 1/16 | 1/16 | 1/8 | 1/4 |
Знайдіть математичне сподівання випадкових величин ξ=Х+У, η=Х–У, λ=ХУ, де Х і У – незалежні випадкові величини.
8.22. Закон розподілу дискретної випадкової величини Х задано таблицею:
| Х | ||||||||
| Р | 1/4 | 1/8 | 1/4 | 1/16 | 1/16 | 1/8 | 1/16 | 1/16 |
а величини У таблицею:
| У | ||||||||
| Р | 1/4 | 1/8 | 1/16 | 1/16 | 1/8 | 1/16 | 1/16 | 1/4 |
Знайдіть математичне сподівання випадкових величин ξ=Х+У, η=Х–У, λ=ХУ, де Х і У – незалежні випадкові величини.
8.23. Закон розподілу дискретної випадкової величини задано таблицею:
| ξ | ||||
| Р | 0.4 | 0.3 | 0.2 | 0.1 |
Знайдіть початкові й центральні моменти перших чотирьох порядків цієї випадкової величини, а також визначте асиметрію і ексцес.
8.24. Дано ряд розподілу дискретної випадкової величини:
| ξ | |||||
| Р | 0.2 | 0.3 | 0.1 | 0.1 | 0.3 |
Знайдіть початкові й центральні моменти перших чотирьох порядків цієї випадкової величини, а також визначте асиметрію і ексцес.
8.25. Два стрільці незалежно один від одного роблять по одному пострілу в мішень. Ймовірність попадання в мішень для першого стрільця р1 для другого р2. Випадкова величина ξ – сумарне число влучень в мішень. Знайдіть закон розподілу ξ, визначте її математичне сподівання Мξ і дисперсію Dξ.
8.26. З корзини, яка містить 4 синіх і 6 білих куль випадковим чином і без повернень виймають три кулі. Випадкова величина ξ – число синіх куль у вибірці. Знайдіть закон розподілу ξ, визначте її математичне сподівання Мξ і дисперсію Dξ.
8.27. З корзини, яка містить 6 синіх і 4 білих куль випадковим чином п’ять разів підряд виймають кулю, причому кожен раз витягнуту кулю повертають в корзину і перемішують. Випадкова величина ξ – число синіх куль у вибірці. Знайдіть закон розподілу ξ, визначте її математичне сподівання Мξ і дисперсію Dξ.
ІІІ. Домашнє завдання (парні задачі).
Практичне заняття №9
Тема: Неперервна випадкова величина. Диференціальна та інтегральна функції розподілу ймовірностей. Числові характери-стики неперервних випадкових величин. Правило трьох сигм
ПЛАН
І. Актуалізація опорних знань.
1. Дайте означення випадкової величини. Яка випадкова величина називається неперервною?
2. Яким чином можна задати закон розподілу неперервної випадкової величини? Диференціальна та інтегральна функції розподілу ймовірностей.
3. Математичне сподівання, дисперсія та середнє квадратичне відхилення неперервної випадкової величини.
4. Моменти, асиметрія і ексцес неперервної випадкової величини.
5. Правило трьох сигм.
ІІ. Розв’язування вправ (непарні задачі).
9.1. Випадкова величина Х задана законом розподілу з щільністю f(х), причому f(х)=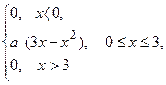 
1) Знайдіть коефіцієнт а; 2) побудуйте графік розподілу щільності у=f(х); 3) знайдіть ймовірність попадання Х в проміжок (1; 2).
9.2. Випадкова величина Х задана функцією розподілу F(x)= 
Обчисліть ймовірності попадання випадкової величини Х в інтервали (1.5; 2.5) і (2.5; 3.5).
9.3. Випадкова величина Х задана функцією розподілу (інтегральною функцією) F(x)=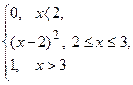 
Обчисліть ймовірності попадання випадкової величини Х в інтервали (1; 2.5) і (2.5; 3.5).
9.4. Випадкова величина Х задана функцією розподілу F(x)= 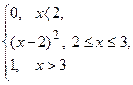Знайдіть щільність розподілу випадкової величини.
9.5. Задана функція розподілу F(x)=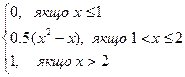 
.
Знайдіть щільність, математичне сподівання та дисперсію. Побудуйте графік функції розподілу та графік щільності.
9.6. Задана функція розподілу F(x)=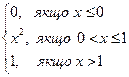 
. Знайдіть щільність, математичне сподівання та дисперсію. Побудуйте графік функції розподілу та графік щільності.
9.7. Задана функція розподілу F(x)=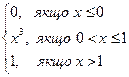 
. Знайдіть щільність, математичне сподівання та дисперсію. Побудуйте графік функції розподілу та графік щільності.
9.8. Задана функція розподілу F(x)= 
. Знайдіть щільність, математичне сподівання та дисперсію. Побудуйте графік функції розподілу та графік щільності.
9.9. Знайдіть ймовірність попадання нормально розподіленої випадкової величини Х в інтервал (12, 14), якщо M(X)=10, D(X)=4.
9.10. Знайдіть ймовірність попадання нормально розподіленої випадкової величини Х в інтервал (15, 25), якщо M(X)=20, σ(X)=5.
9.11. Випадкова величина Х задана щільністю розподілу f(x)=2cos2x в інтервалі (0; π/4); поза цим інтервалом f(x)=0. Знайдіть а) моду; б) медіану Х.
9.12. Випадкова величина Х в інтервалі (2; 4) задана щільністю розподілу f(x)=–(3/4)х2+(9/2)х–6; поза цим інтервалом f(x)=0. Знайдіть моду, математичне сподівання і медіану величини Х.
9.13. Випадкова величина Х в інтервалі (3; 5) задана щільністю розподілу f(x)=–(3/4)х2+6х–45/4; поза цим інтервалом f(x)=0. Знайдіть моду, математичне сподівання і медіану величини Х.
9.14. Випадкова величина Х в інтервалі (–1; 1) задана щільністю розподілу f(x)=1/(π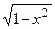 
); поза цим інтервалом f(x)=0. Знайдіть а) моду; б) медіану Х.
9.15. Випадкова величина Х задана щільністю розподілу f(x)=0.5x в інтервалі (0; 2); поза цим інтервалом f(x)=0. Знайдіть початкові й центральні моменти перших чотирьох порядків, асиметрію і ексцес.
9.16. Випадкова величина Х задана щільністю розподілу f(x)=2x в інтервалі (0; 1); поза цим інтервалом f(x)=0. Знайдіть початкові й центральні моменти перших чотирьох порядків, асиметрію і ексцес.
ІІІ. Самостійна робота.
IV.Домашнє завдання (парні задачі), інд. творче завдання.