 |
|
Приклади розв’язування типових задач
Задача 3.1. Є три корзини з кульками. У першій корзині 6 білих і 1 синя кулька, у другій – 3 білих і 4 синіх, у третій – 2 білих і 5 синіх кульок. Дівчинка вибирає одну з корзин і виймає з неї кульку. Знайти ймовірність того, що: 1) кулька виявиться білою; 2) біла кулька буде вийнята з другої корзини.
Розв’язання. 1) Позначимо через А подію: „поява білої кульки”. Вийняти кульку можна з трьох корзин, тобто можливі три випадки (три гіпотези). Позначимо їх: Н1 – кулька вийнята з першої корзини, Н2 – з другої, Н3 – з третьої. Ймовірності гіпотез дорівнюють Р(Н1)=Р(Н2)=Р(Н3)=1/3. Умовні ймовірності події А відповідно дорівнюють: Р(А/Н1)=6/7 – ймовірність вийняти білу кульку з першої корзини, Р(А/Н2)=3/7 – з другої, Р(А/Н3)=2/7 – з третьої.
Тоді за формулою повної ймовірності отримаємо:
Р(А)=Р(Н1)Р(А/Н1)+Р(Н2)Р(А/Н2)+Р(Н3)Р(А/Н3)= 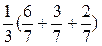 =
= 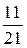 .
.
2) Для визначення ймовірності того, що біла кулька вийнята з другої корзини, використаємо формулу Байєса:
Р(Н2/А)=  .
.
Відповідь:1) 11/21; 2) 3/11.
Індивідуальні завдання для самостійної роботи
1. При переливанні крові потрібно враховувати групу крові донора й хворого. Людині, що має четверту групу крові, можна перелити кров будь-якої групи; людині з другою або третьою групою крові можна перелити кров або тої ж групи, або першої; людині з першою групою крові можна перелити тільки кров першої групи. Серед населення 33,7% мають першу, 37,5% – другу, 20,9% – третю і 7,9% – четверту групу крові. Знайти ймовірність того, що випадково взятому хворому можна перелити кров випадково взятого донора.
2. Відомо, що в партії з 600 деталей 200 виготовлені на першому, 250 – на другому і 150 – на третьому заводі. Відомі також ймовірності 0,97, 0,91, 0,93 того, що деталь виявиться стандартною при виготовленні її відповідно 1-им, 2-им та 3-ім заводами. Знайти ймовірність того, що навмання вибрана з даної партії деталь виявиться стандартною. Яка ймовірність того, що навмання вибрана деталь виготовлена на першому заводі, якщо вона виявилася стандартною?
3. Є 2 партії виробів по 20 і 15 штук, причому в кожній партії один виріб дефектний. Виріб, взятий навмання з другої партії, перекладений в першу, після чого вибирається випадковим чином виріб з першої партії. Визначити, яка ймовірність обрати з першої партії бракований виріб.
4. Стрілок А влучає в мішень з ймовірністю р1=0,6, стрілок В – з ймовірністю р2=0,5, а стрілок С – з ймовірністю р3=0,4. Стрільці зробили залп по мішені. Відомо, що є два влучення. Що більш імовірно: влучив С в мішень чи ні?
5. З урни яка містить 7 білих і 8 чорних куль, загублено одну кулю. Для того щоб визначити склад куль в урні, з неї взяли дві кулі, які виявилися білими. Обчислити ймовірність того , що загублена куля біла?
6. Три мисливці одночасно зробили по одному пострілу у ведмедя. Ведмедя вбито однією кулею. Яка ймовірність того, що ведмедя вбито першим, другим, або третім мисливцем, якщо ймовірність влучення для них дорівнюють відповідно р1=0,2, р2=0,4, р3=0,6?
7. З урни яка містить 3 білих та 2 чорних кулі, перекладено дві кулі до урни, яка містить 4 білих та 4 чорних кулі. Яка ймовірність того, що з другої урни після такого перекладання буде взято білу кулю?
8. Два стрільці незалежно один від одного роблять по одному пострілу по мішені. Ймовірність влучення першого 0,8, а другого – 0,4. Відомо, що є одне влучення. Знайти ймовірність того, що у мішень влучив перший стрілок.
9. На фабриці виготовляють гвинти. Перша машина виготовляє 25%, друга – 35%, третя – 40% усіх виробів. Частка браку відповідно 5%, 4% і 2%. а) Яка ймовірність того, що випадково вибраний гвинт бракований? б) Випадково вибраний гвинт виявився бракованим. Яка ймовірність того, що його зроблено першою, другою, третьою машинами?
10. При масовому виробництві деякого виробу ймовірність того, що він виявиться стандартним, дорівнює 0,95. Для контролю проводиться деяка спрощена перевірка стандартності виробу, яка дає позитивний результат у 98% для стандартних виробів та у 4% – для нестандартних. Яка ймовірність стандартності виробу, що витримав спрощену перевірку?
11. Є 3 корзини: у першій – 10 білих та 5 чорних, у другій – 7 білих і 4 чорних, у третій – 12 білих кульок. Хлопчик вибирає навмання одну з корзин та виймає кульку, вона – біла. Знайти ймовірність того, що ця кулька вийнята з першої, другої чи третьої корзини.
12. У групі 18 студентів, які прийшли на екзамен. 5 підготовлені відмінно, 7 – добре, 4 – задовільно та 2 – незадовільно. У екзаменаційних білетах всього 20 питань. відмінно підготовлений студент може дати відповідь на всі 20 питань, добре підготовлений – на 16, задовільно – на 10, незадовільно – на 5. Викликаний навмання студент відповів на всі три довільно заданих питання. Знайти ймовірність того, що цей студент підготовлений: а) відмінно; б) незадовільно.
13. З першого автомату на збірку потрапляє 50, з другого – 15, з третього – 35 деталей. Серед деталей першого автомату 0,2% бракованих, другого – 0,3%, третього – 0,5%. Знайти ймовірність того, що деталь, яка поступила на збірку, бракована.
14. Відомо, що 94% продукції, яка випускається, задовольняє стандарт. Схема контролю признає придатною стандартну продукцію з ймовірністю 0,96 та нестандартну – з ймовірністю 0,04. Визначити ймовірність того, що виріб, пройшовши контроль, задовольняє стандарт.
15. Характеристика матеріалу, взятого для виготовлення продукції з ймовірностями 0,09, 0,16, 0,25, 0,25, 0,16 та 0,09, може знаходитися у шести різних інтервалах. В залежності від властивостей матеріалу ймовірності отримання першосортної продукції дорівнюють відповідно 0,2, 0,3, 0,4, 0,4, 0,3, 0,2. Визначити ймовірність отримання першосортної продукції.
16. На збірку надходять шестерні з трьох автоматів. Перший дає 25%, другий – 30% і третій – 45% шестерень, які надходять на збірку. Перший допускає 0,1% браку шестерень, другий – 0,2%, третій – 0,3%. Знайти ймовірність надходження на збірку бракованої шестерні (P1) та ймовірність того, що виявлена бракована шестерня виготовлена першим автоматом (P2).
17. Два автомати виготовляють деталі, які надходять на загальний конвеєр. Ймовірність отримання нестандартної деталі на першому автоматі дорівнює 0,075, на другому – 0,09. Виробництво другого автомата вдвічі більше, ніж першого. Знайти ймовірність того, що взята навмання з конвеєра деталь нестандартна.
18. Деталь одночасно підлягала обробці трьома інструментами, в результаті чого була визнана непридатною. Визначити ймовірність того, що деталь була непридатною у результаті обробки першим, другим і третім інструментом, якщо ймовірності несправності для них відповідно дорівнюють 0,2, 0,45, 0,35.
19. Деталі потрапляють для перевірки на стандартність до одного з двох контролерів. Ймовірність того, що придатна деталь буде признана стандартною першим контролером дорівнює 0,04, а другим – 0,98. Придатна деталь при перевірці була признана стандартною. Знайти ймовірність того, що цю деталь перевірив перший контролер.
20. Радіолампа, встановлена у телевізор, може належати до однієї з трьох партій з ймовірностями Р1 = 0,35, Р2 = 0,5, Р3 = 0,15. Ймовірність того, що лампа пропрацює певну кількість годин, для цих партій дорівнює відповідно: 0,15, 0,21, 0,45. Визначити ймовірність того, що лампа пропрацює задану кількість годин.
21. Для сигналізації про те, що режим роботи автоматичної лінії відхиляється від нормального, використовується індикатор. Він належить з ймовірністю 0,2, 0,3 і 0,5 до одного з трьох типів, для яких ймовірність спрацювання при порушенні нормальної роботи лінії дорівнюють відповідно 1, 0,75, 0,4. Від індикатора отримано сигнал. До якого типу ймовірніше всього належить індикатор?
22. По лінії зв’язку передаються два сигнали А і В відповідно з ймовірностями 0,84 і 0,16. Із-за перешкод 1/6 сигналів А спотворюються і приймаються як В-сигнали, а 1/8 частина переданих В-сигналів приймається, як А-сигнали. Знайти ймовірність того, що в приймальному пункті з’явиться А-сигнал. Яка ймовірність того, що саме його передали?
23. Три підприємства постачають магазину алюмінієві віконні рами. Перше підприємство постачає 35%, друге – 50%, третє – 15% рам. Перше підприємство виготовляє 2% дефектних рам, друге – 1%, а трете – 0,3%. Перевіряється одна рама і виявляється, що вона дефектна. Яка ймовірність того, що її поставником було друге підприємство?
24. У коробці можуть бути сірники без чорної голівки. Відомо, що 40% коробок не мають дефектних сірників, 30% мають один дефектний сірник, 25% – два і 50% – три дефектні сірники. Дана коробка має дефектні сірники. Яка ймовірність, що в коробці виявиться два дефектні сірники?
25. Радист тричі викликає кореспондента. Ймовірність того, що буде прийнято перший виклик, дорівнює 0,2, другий – 0,3, третій – 0,4. За вимогами прийому події, які полягають в тому, що даний виклик буде почуто, незалежні. Знайти ймовірність того, що кореспондент взагалі почує виклик.
26. Є дві партії деталей по 120 і 80 штук, причому в кожній партії одна деталь бракована. Деталь, узята навмання з першої партії, перекладена в другу, після чого вибирається навмання деталь з другої партії. Визначити ймовірність вибору бракованої деталі з другої партії.
27. У групі спортсменів 20 лижників, 6 велосипедистів та 4 бігуна. Ймовірність виконати норму така: для лижника – 0,9, для велосипедиста – 0,8 та для бігуна – 0,75. Знайти ймовірність того, що спортсмен, вибраний навмання, виконає норму.
28. У телевізійному ательє є 4 кінескопи. Ймовірність того, що кінескоп витримає гарантійний термін служби, відповідно дорівнюють 0,8, 0,85, 0,9, 0,95. Знайти ймовірність того, що взятий навмання кінескоп витримає гарантійний термін служби.
29. Є 3 корзини: у першій – 12 білих та 7 червоних, у другій – 11 білих і 4 червоних, у третій – 10 білих кульок. Хлопчик вибирає навмання одну з корзин та виймає кульку, вона – біла. Знайти ймовірність того, що ця кулька вийнята з першої, другої чи третьої корзини.
30. Відомо, що в партії з 500 деталей 100 виготовлені на першому, 250 – на другому і 150 – на третьому заводі. Відомі також ймовірності 0,95, 0,92, 0,94 того, що деталь виявиться стандартною при виготовленні її відповідно 1-им, 2-им та 3-ім заводами. Знайти ймовірність того, що навмання вибрана з даної партії деталь виявиться стандартною. Яка ймовірність того, що навмання вибрана деталь виготовлена на першому заводі, якщо вона виявилася стандартною?