 |
|
Приклади розв’язування типових задач
Задача 5.1.Розподіл дискретної випадкової величини Х задано таблицею:
| Х | ||||
| Р | 0,4 | 0,2 | 0,1 | 0,3 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення.
Розв’язання. Математичне сподівання випадкової величини Х обчислимо за формулою:
М(Х)=х1р1+ х2р2+ х3р3+ х4р4=2·0,4+4·0,2+8·0,1+10·0,3=5,4.
Запишемо розподіл величини Х2:
| Х2 | ||||
| Р | 0,4 | 0,2 | 0,1 | 0,3 |
Тоді дисперсія випадкової величини Х легко обчислюється за формулою:
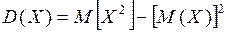=4·0,4+16·0,2+64·0,1+100·0,3–(5,4)2=
=1,6+3,2+6,4+30–29,16=12,04.
Середнє квадратичне відхилення рівне:
= 
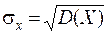»3,47.
Відповідь: МХ=5,4; DХ=12,04; σх»3,47.
Задача 5.2.Випадкова величина Х розподілена за законом зі щільністю р(x), причому
при x < 0,
при 0 ≤ х ≤ 3,
при х > 3.
Потрібно 1)Знайти коефіцієнт а; 2) побудувати графік розподілу щільності y=р(x); 3) знайти ймовірність попадання Х в проміжок [1;2].
Розв’язання. 1) Так як усі значення даної випадкової величини містяться у відрізку [0; 3], то
, звідки
або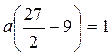 
, тобто 
.
2) Графіком функції р(x) на проміжку [0; 3] є частина параболи 
, а поза цим проміжком – сама вісь абсцис.
3) Ймовірність попадання випадкової величини Х в проміжок [1; 2] знайдеться з рівності:
.
Відповідь: ; Р(1<Х<2)=13/27.
Задача 5.3.Випадкова величина Х задана щільністю розподілу:
при x < 0,
при 0 ≤ х ≤ 1,
при х > 1.
Побудувати функцію розподілу F(x).
Розв’язання. Якщо x < 0, то р(х)=0, тому F(x)=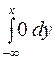 
=0.
Якщо 0 ≤ х ≤ 1, то F(x)= 
= х.
Якщо х > 1, то F(x)=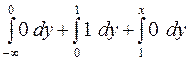 
= 1.
Отже,
Відповідь: функція розподілу
Індивідуальні завдання для самостійної роботи
Варіант 1
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 1.1 | 1.3 | 1.5 | 1.7 | 1.9 |
| Р | 0.2 | 0.3 | 0.1 | 0.1 | 0.3 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 2
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 |
| Р | 0.3 | 0.1 | 0.2 | 0.3 | 0.1 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
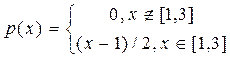Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 3
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 1.5 | 1.7 | 1.9 | 2.1 | 2.3 |
| Р | 0.3 | 0.2 | 0.1 | 0.2 | 0.2 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 4
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 1.4 | 1.6 | 1.8 | 2.0 | 2.2 |
| Р | 0.1 | 0.3 | 0.1 | 0.1 | 0.4 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
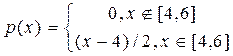Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 5
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 1.5 | 1.6 | 1.8 | 1.9 | 2.1 |
| Р | 0.2 | 0.4 | 0.1 | 0.1 | 0.2 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
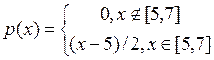Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 6
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 1.6 | 1.7 | 1.9 | 2.2 | 2.3 |
| Р | 0.1 | 0.4 | 0.1 | 0.2 | 0.2 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
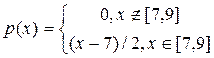Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 7
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 1.8 | 2.1 | 2.3 | 2.4 | 2.6 |
| Р | 0.2 | 0.2 | 0.1 | 0.1 | 0.4 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
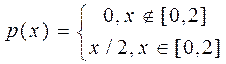Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 8
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 1.9 | 2.1 | 2.2 | 2.3 | 2.5 |
| Р | 0.2 | 0.3 | 0.1 | 0.1 | 0.3 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 9
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 1.9 | 2.0 | 2.3 | 2.4 | 2.6 |
| Р | 0.3 | 0.3 | 0.1 | 0.1 | 0.2 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 10
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 2.1 | 2.2 | 2.3 | 2.5 | 2.7 |
| Р | 0.2 | 0.2 | 0.2 | 0.3 | 0.1 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 11
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 0.3 | 0.5 | 0.6 | 0.8 | 0.9 |
| Р | 0.3 | 0.2 | 0.2 | 0.1 | 0.2 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 12
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 0.4 | 0.5 | 0.7 | 0.8 | 1.1 |
| Р | 0.4 | 0.1 | 0.1 | 0.3 | 0.1 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 13
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 0.6 | 0.8 | 0.9 | 2.1 | 2.3 |
| Р | 0.2 | 0.2 | 0.1 | 0.2 | 0.3 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
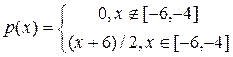Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 14
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 2.2 | 2.4 | 2.6 | 2.7 | 3.0 |
| Р | 0.2 | 0.3 | 0.1 | 0.2 | 0.2 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 15
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 2.9 | 3.1 | 3.2 | 3.3 | 3.5 |
| Р | 0.2 | 0.3 | 0.1 | 0.1 | 0.3 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 16
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 3.0 | 3.1 | 3.2 | 3.3 | 3.7 |
| Р | 0.3 | 0.1 | 0.3 | 0.1 | 0.3 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 17
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 3.2 | 3.3 | 3.5 | 3.7 | 3.9 |
| Р | 0.1 | 0.4 | 0.1 | 0.1 | 0.3 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 18
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 3.3 | 3.5 | 3.7 | 3.8 | 3.9 |
| Р | 0.1 | 0.4 | 0.2 | 0.1 | 0.2 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 19
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 3.5 | 3.6 | 3.8 | 3.9 | 4.1 |
| Р | 0.4 | 0.1 | 0.1 | 0.1 | 0.3 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 20
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 3.6 | 3.7 | 3.9 | 4.1 | 4.2 |
| Р | 0.3 | 0.2 | 0.1 | 0.3 | 0.1 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
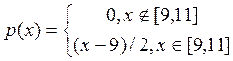Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 21
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 3.8 | 3.9 | 4.1 | 4.2 | 4.4 |
| Р | 0.3 | 0.2 | 0.1 | 0.1 | 0.3 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 22
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 3.9 | 4.0 | 4.1 | 4.3 | 4.5 |
| Р | 0.2 | 0.3 | 0.3 | 0.1 | 0.1 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
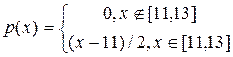Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 23
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 4.0 | 4.1 | 4.2 | 4.3 | 4.4 |
| Р | 0.2 | 0.3 | 0.1 | 0.1 | 0.3 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 24
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 4.2 | 4.3 | 4.5 | 4.6 | 4.7 |
| Р | 0.2 | 0.3 | 0.1 | 0.1 | 0.3 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
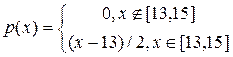Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 25
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 4.3 | 4.4 | 4.5 | 4.7 | 4.8 |
| Р | 0.3 | 0.3 | 0.1 | 0.1 | 0.2 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 26
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 4.3 | 4.4 | 4.5 | 4.6 | 4.8 |
| Р | 0.2 | 0.3 | 0.1 | 0.2 | 0.2 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 27
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | 4.4 | 4.5 | 4.6 | 4.7 | 4.9 |
| Р | 0.2 | 0.1 | 0.3 | 0.1 | 0.3 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 28
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | -1.2 | -1.1 | 0.5 | 0.6 | 0.7 |
| Р | 0.3 | 0.3 | 0.1 | 0.1 | 0.2 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
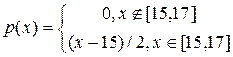Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 29
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | -2.2 | -2.0 | -1.6 | -1.3 | -1.1 |
| Р | 0.2 | 0.1 | 0.3 | 0.1 | 0.3 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
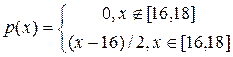Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
Варіант 30
1. Розподіл дискретної випадкової величини задано таблицею:
| Х | -3.2 | -3.0 | -2.5 | -2.3 | -1.5 |
| Р | 0.3 | 0.3 | 0.1 | 0.2 | 0.2 |
Знайти математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення, асиметрію і ексцес.
2. Абсолютно неперервна випадкова величина Х має щільність:
,
Знайти функцію розподілу Х, математичне сподівання МХ, дисперсію DХ, середнє квадратичне відхилення. Побудувати графіки щільності та функції розподілу випадкової величини Х.
ПИТАННЯ ДО КОЛОКВІУМІВ
Колоквіум № 1
1. Простiр елементарних подiй, випадковi подiї. Дії над подіями.
2. Статистичне та класичне означення ймовiрностi.
3. Аксiоми ймовiрностей. Властивостi ймовiрностi.
4. Геометричні ймовірності.
5. Теореми додавання та множення ймовірностей.
6. Умовна ймовipність. Незалежнi подiї.
7. Формули повної ймовiрностi та Байєса.
8. Повторні незалежні випробування. Схема і формула Бернуллi.
9. Теорема Пуассона.
10. Локальна та iнтегральна теореми Муавра-Лапласа.
Колоквіум № 2
1. Означення та основнi типи випадкових величин. Числовi характеристики випадкових величин.
2. Дискретнi випадковi величини. Закон розподілу випадкової величини.
3. Математичне сподiвання дискретної випадкової величини та його властивостi.
4. Диперсiя дискретної випадкової величини та її властивостi. Середнє квадратичне відхилення.
5. Моменти, асиметрія та ексцес дискретної випадкової величини.
6. Неперервнi випадковi величини. Функцiя розподiлу, щiльнiсть та їх властивості.
7. Математичне сподiвання неперервної випадкової величини та його властивостi.
8. Диперсiя неперервної випадкової величини та її властивостi. Середнє квадратичне відхилення.
9. Моменти, асиметрія та ексцес неперервної випадкової величини.
10. Бiномiальний, геометричний, пуассонiвський розподiли.
11. Рiвномiрний, показниковий, нормальний розподiли ймовірностей.
12. Нормована випадкова величина. Правило трьох сигм.
ЛІТЕРАТУРА
1. Волков Ю.І., Войналович Н.М. Елементи дискретної математики: Навчальний посібник. – Кіровоград: РВГ ІЦ КДПУ ім. В.Винниченка, 1999. – 173 с.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. – М.: Высш. шк., 2003. – 405 с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов. – М.: Высш. шк., 2003. – 479 с.
4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: Учеб. пособие для студентов втузов. В 2-х ч. Ч.ІІ. – М.: Высш. шк.., 1986. – 415 с.
5. Жалдак М.І. Початки теорії ймовірностей. – К.: Рад. шк., 1978. – 143 с
6. Жлуктенко В.І., Наконечний С.І. Теорія ймовірностей та математична статистика: Навч.-метод. посібник. У 2 ч. – Ч. І. Теорія ймовірностей. – К.: КНЕУ, 2000. – 304 с.
7. Климчук В.І. Методика розв’язування задач з теорії імовірностей та математичної статистики. – К., 1970. – 80 с.
8. Конет І.М. Теорія ймовірностей та математична статистика в прикладах і задачах. – Кам’янець–Подільський: Абетка, 2001. – 220 с.
9. Черняк О.І., Обушна О.М., Ставицький А.В. Теорія ймовірностей та математична статистика: Збірник задач: Навч. посіб. – К.: Знання, КОО, 2002. – 199с.
10. Шкіль М.І. та ін. Алгебра і початки аналізу: Проб. підруч. для 10-11 кл. серед. шк. / М.І. Шкіль, З.І. Слєпкань, О.С. Дубинчук. – К.: Зодіак-ЕКО, 1995. – 608 с.