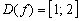 |
|
Область определения функции с логарифмом
Третья распространённая функция – логарифм. В качестве образца я буду рисовать натуральный логарифм, который попадается примерно в 99 примерах из 100. Если некоторая функция содержит логарифм 
, то в её область определения должны входить только те значения «икс», которые удовлетворяют неравенству 
. Если логарифм находится в знаменателе: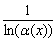 
, то дополнительно накладывается условие 
(так как 
).
Найти область определения функции
Решение: в соответствии с вышесказанным составим и решим систему:
Графическое решение для чайников:
Ответ: область определения: 
Остановлюсь ещё на одном техническом моменте – у меня ведь не указан масштаб и не проставлены деления по оси. Возникает вопрос: как выполнять подобные чертежи в тетради на клетчатой бумаге? Отмерять ли расстояние между точками по клеточкам строго по масштабу? Каноничнее и строже, конечно, масштабировать, но вполне допустим и схематический чертёж, принципиально отражающий ситуацию.
Найти область определения функции
Как видите, в царстве логарифмов всё очень похоже на ситуацию с квадратным корнем: функция 
. определена на интервалах 
, а функция 
на интервале 
. Неловко уже и говорить, функции типа 
определены на всей числовой прямой.
Полезная информация: интересна типовая функция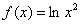 
, она определена на всей числовой прямой кроме точки 
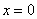. Согласно свойству логарифма 
, «двойку» можно вынести множителем за пределы логарифма, но, чтобы функция не изменилась, «икс» необходимо заключить под знак модуля: 
. Вот вам и ещё одно «практическое применение» модуля = ). Так необходимо поступать в большинстве случаев, когда вы снОситечётнуюстепень, например: 
. Если же основание степени заведомо положительно, например, 
, то в знаке модуля отпадает необходимость и достаточно обойтись круглыми скобками: 
.
Найти область определения функции
Решение: в данной функции у нас присутствует и корень и логарифм.
Подкоренное выражение должно быть неотрицательным: 
, а выражение под знаком логарифма – строго положительным: 
. Таким образом, необходимо решить систему:
Многие из вас прекрасно знают или интуитивно догадываются, что решение системы должно удовлетворять каждому условию.
Исследуя расположение параболы 
относительно оси 
, приходим к выводу, что неравенству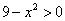 
удовлетворяет интервал 
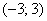(синяя штриховка):
Неравенству , очевидно, соответствует «красный» полуинтервал 
.
Поскольку оба условия должны выполняться одновременно, то решением системы является пересечение данных интервалов. «Общие интересы» соблюдены на полуинтервале 
.
Ответ: область определения: 
Типовое неравенство 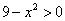, как демонстрировалось в Примере №8, нетрудно разрешить и аналитически.
Найденная область определения не изменится для «похожих функций», например, для 
или 
. Также можно добавить какие-нибудь непрерывные на 
функции, например: 
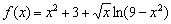, или так: 
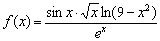, или даже так: 
. Как говорится, корень и логарифм – вещь упрямая. Единственное, если одну из функций «сбросить» в знаменатель, то область определения изменится
Найти область определения функции
Решение: составим и решим систему:
Все действия уже разобраны по ходу статьи. Изобразим на числовой прямой интервал, соответствующий неравенству 
и, согласно второму условию, исключим две точки:
Значение 
оказалось вообще не при делах.
Ответ: область определения 
Области определения функций
с тангенсами, котангенсами, арксинусами, арккосинусами
Перед изучением параграфа рекомендую вновь вернуться к первой статье о графиках, чтобы освежить визуальную и аналитическую информацию о перечисленных в заголовке функциях.
Если в некоторую функцию входит 
, то из её области определения исключаютсяточки 
, где Z – множество целых чисел. В частности, как отмечалось в статье Графики и свойства элементарных функций, у функции 
выколоты следующие значения:
То есть, область определения тангенса: 
.
Найти область определения функции
Решение: в данном случае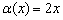 
и в область определения не войдут следующие точки:
Скинем «двойку» левой части в знаменатель правой части:
В результате 
:
Ответ: область определения: 
.
В принципе, ответ можно записать и в виде объединения бесконечного количества интервалов, но конструкция получится весьма громоздкой:
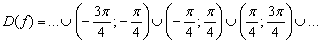
Аналитическое решение полностью согласуется с геометрическим преобразованием графика: если аргумент функции умножить на 2, то её график сожмётся к оси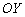 
в два раза. Заметьте, как у функции уполовинился период, и точки разрываучастились в два раза. Тахикардия.
Похожая история с котангенсом. Если в некоторую функцию входит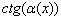 
, то из её области определения исключаются точки 
. В частности, для функции 
автоматной очередью расстреливаем следующие значения:
Иными словами: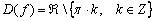 
Найти область определения функции
Решение: составим двойное неравенство:
Действия с двойным неравенством очень похожи на действия с «обычным» одинарным неравенством. Конечная цель преобразований – добиться, чтобы в середине остался только «икс».
Сначала избавимся в средней части от константы, для этого вычтем из каждой части неравенства «тройку»:
Умножим все три части неравенства на –1. Поскольку множитель отрицателен, то знакисамих неравенств необходимо «развернуть» в противоположную сторону:
Умножим все части неравенства на 
:
Запишем ответ, переставив знаки неравенств в привычном порядке, а то по-арабски как-то получилось – от «единицы» до «двух» справа налево.
Ответ: область определения: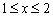 
или 