 |
|
Что такое нули функции и что такое интервалы знакопостоянства функции?
Рассмотрим некоторую функцию 
.
1) Точки, в которых график пересекает ось 
, называют нулями функции. Чтобы найти нули функции нужно решить уравнение 
, то есть найти те значения «икс», при которых функция обращается в ноль. В следующем условном примере нули функции 
обозначены красными точками:
Очевидно, что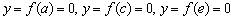 
. Заметьте, что точка 
не является нулём функции, поскольку не входит в её область определения.
2) Интервал знакопостоянства – это интервал, в каждой точке которого функция положительна либо отрицательна.
В нашем случае функция положительна на интервалах 
, то есть для любого значения «икс» любого из перечисленных интервалов справедливо строгое неравенство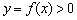 
. Или совсем просто – график функции на таких интервалах расположен ВЫШЕ оси абсцисс.
На интервалах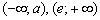 
функция отрицательна, то есть любому значению «икс», принадлежащему этим интервалам соответствует строгое неравенство 
, и график функции расположен НИЖЕ оси .
Компактная запись перечисленных фактов выглядит так:
, если 
;
, если 
.
Строки можно переставить местами, это не имеет принципиального значения, лично я привык сначала указывать интервалы, на которых функция положительна.
Что можно сказать об интервале 
? Только то, что функция не определена на данном интервале, и, разумеется, о знакопостоянстве речи не идёт вообще.
Примечание: в математике более широким является термин «промежуток», который включает в себя не только интервал, но и полуинтервал либо отрезок. Полуинтервалы и отрезки знакопостоянства часто встречаются у кусочно-заданных функций. В частности, если на вышеуказанном чертеже «закрасить» точку с абсциссой 
, то получим промежуток (в данном случае – полуинтервал) знакопостоянства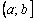 
. Однако далее будут рассматриваться «обычные» функции, обладающие только интервалами знакопостоянства, поэтому в термине «промежуток знакопостоянства» нет особой нужды.