 |
|
Первое достаточное условие экстремума,
которое вкратце формулируется следующим образом: пусть функция дифференцируема в некоторой окрестности критической точки 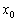 . Тогда:
. Тогда:
– если при переходе через точку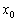 производная меняет знак с «плюса» на «минус», то в данной точке функция достигает максимума;
производная меняет знак с «плюса» на «минус», то в данной точке функция достигает максимума;
– если при переходе через точку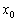 производная меняет знак с «минуса» на «плюс», то в данной точке функция достигает минимума.
производная меняет знак с «минуса» на «плюс», то в данной точке функция достигает минимума.
Тут всё очень и очень наглядно, представьте – функция росла-росла-росла, и после прохождения некоторого рубежа вдруг стала убывать. Максимум. Во втором случае график шёл-шёл-шёл «сверху вниз», а при переходе через точку 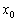 развернулся в противоположную сторону. Минимум.
развернулся в противоположную сторону. Минимум.
Исходя из вышесказанного, вытекает логичное решение: на числовой прямой нужно отложитьточки разрыва функции, критические точки и определить знаки производной на интервалах, которыевходят в область определения функции.
В рассматриваемом примере с непрерывностью на  всё тип-топ, поэтому работаем только с найдёнными критическими точками.
всё тип-топ, поэтому работаем только с найдёнными критическими точками.
Напрашивается метод интервалов, который уже применялся для определенияинтервалов знакопостоянства функции. Так почему бы его не использовать для производной? Ведь производная тоже простая смертная функция, найдёшь её – и делай всё, что хочешь.
Внимание! Сейчас мы работаем с ПРОИЗВОДНОЙ, а не с самой функцией!
Перед нами парабола  , ветви которой направлены вниз, и многим читателям уже понятны знаки производной, но ради повторения снова пройдёмся по всем этапам метода интервалов. Отложим на числовой прямой найденные критические точки:
, ветви которой направлены вниз, и многим читателям уже понятны знаки производной, но ради повторения снова пройдёмся по всем этапам метода интервалов. Отложим на числовой прямой найденные критические точки:

I) Берём какую-нибудь точку интервала  и находим значение производной в данной точке. Удобнее всего выбрать
и находим значение производной в данной точке. Удобнее всего выбрать 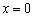 :
:
 , значит, производная отрицательна на всём интервале
, значит, производная отрицательна на всём интервале  .
.
II) Выбираем точку  , принадлежащую интервалу
, принадлежащую интервалу  , и проводим аналогичное действие:
, и проводим аналогичное действие:
 , следовательно,
, следовательно,  на всём интервале
на всём интервале  .
.
III) Вычислим значение производной в наиболее удобной точке  последнего интервала:
последнего интервала:
 , поэтому
, поэтому  в любой точке интервала
в любой точке интервала 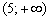 .
.
В результате получены следующие знаки производной:

Время собирать урожай!
На интервалах  производная отрицательна, значит, САМА ФУНКЦИЯ
производная отрицательна, значит, САМА ФУНКЦИЯ  на данных интервалахубывает, и её график идёт «сверху вниз». На среднем интервале
на данных интервалахубывает, и её график идёт «сверху вниз». На среднем интервале  , значит, функция возрастает на
, значит, функция возрастает на  , и её график идёт «снизу вверх».
, и её график идёт «снизу вверх».
При переходе через точку  производная меняет знак с «–» на «+», следовательно, в этой точке функция достигает минимума:
производная меняет знак с «–» на «+», следовательно, в этой точке функция достигает минимума:

При переходе же через точку  производная меняет знак с «+» на «–», и функция достигает максимума в данной точке:
производная меняет знак с «+» на «–», и функция достигает максимума в данной точке:
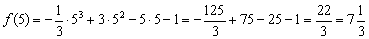
Ответ: функции возрастает на интервале  и убывает на интервалах
и убывает на интервалах  . В точке
. В точке  функция достигает минимума:
функция достигает минимума: 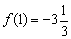 , а в точке
, а в точке  – максимума:
– максимума: 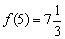
Остерегайтесь сокращенной записи  . Под значками
. Под значками  обычно понимают минимальное и максимальное значение, а это, как пояснялось выше, далеко не то же самое, что минимум и максимум.
обычно понимают минимальное и максимальное значение, а это, как пояснялось выше, далеко не то же самое, что минимум и максимум.
Пример так тщательно провёрнут через мясорубку, что грех не привести графическое изображение всех событий. Незнакомец теоретической части статьи снимает шляпу:

Что произошло? На первом этапе мы нашли производную 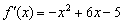 и критические точки
и критические точки  (в которых парабола пересекает ось абсцисс). Затем методом интервалов было установлено, где
(в которых парабола пересекает ось абсцисс). Затем методом интервалов было установлено, где  (парабола ниже оси) и
(парабола ниже оси) и  (парабола выше оси). Таким образом, с помощью производной мы узнали интервалы возрастания/убывания и экстремумы «синей» функции.
(парабола выше оси). Таким образом, с помощью производной мы узнали интервалы возрастания/убывания и экстремумы «синей» функции.
Помимо 1-го достаточного условия экстремума существует и другое, так называемое 2-ое достаточное условие экстремума. Однако для исследования функцийоно малоинформативно и больше используется в экстремальных задачах.
В начале первой статьи о графиках функции я рассказывал, как быстро построить параболу на примере  : «…берём первую производную и приравниваем ее к нулю:
: «…берём первую производную и приравниваем ее к нулю:  …Итак, решение нашего уравнения:
…Итак, решение нашего уравнения:  – именно в этой точке и находится вершина параболы…».
– именно в этой точке и находится вершина параболы…».
Исследовать функцию с помощью первой производной
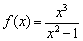
Обратите внимание, как вариативно можно переформулировать фактически одно и то же задание.
Решение:
1) Функция терпит бесконечные разрывы в точках  .
.
2) Детектируем критические точки. Найдём первую производную и приравняем её к нулю:
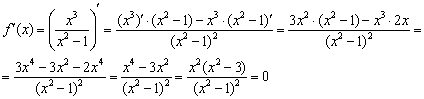
Решим уравнение  . Дробь равна нулю, когда её числитель равен нулю:
. Дробь равна нулю, когда её числитель равен нулю:

Таким образом, получаем три критические точки:
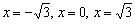
3) Откладываем на числовой прямой ВСЕ обнаруженные точки и методом интерваловопределяем знаки ПРОИЗВОДНОЙ:

Напоминаю, что необходимо взять какую-нибудь точку интервала, вычислить в ней значение производной  и определить её знак. Выгоднее даже не считать, а «прикинуть» устно. Возьмём, например, точку
и определить её знак. Выгоднее даже не считать, а «прикинуть» устно. Возьмём, например, точку  , принадлежащую интервалу
, принадлежащую интервалу  , и выполним подстановку:
, и выполним подстановку: 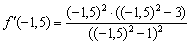 .
.

Два «плюса» и один «минус» дают «минус», поэтому 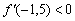 , а значит, производная отрицательна и на всём интервале
, а значит, производная отрицательна и на всём интервале  .
.
Действие, как вы понимаете, нужно провести для каждого из 6-ти интервалов. Кстати, обратите внимание, что множитель числителя 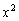 и знаменатель
и знаменатель 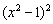 строго положительны для любой точки любого интервала, что существенно облегчает задачу.
строго положительны для любой точки любого интервала, что существенно облегчает задачу.
Итак, производная сообщила нам, что САМА ФУНКЦИЯ 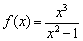 возрастает на
возрастает на  и убывает на
и убывает на  . Однотипные интервалы удобно скреплять значком объединения
. Однотипные интервалы удобно скреплять значком объединения  .
.
В точке  функция достигает максимума:
функция достигает максимума: 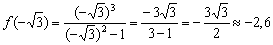
В точке 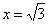 функция достигает минимума:
функция достигает минимума: 
Подумайте, почему можно заново не пересчитывать второе значение ;-)
При переходе через точку 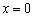 производная не меняет знак, поэтому у функции там НЕТ ЭКСТРЕМУМА – она как убывала, так и осталась убывающей.
производная не меняет знак, поэтому у функции там НЕТ ЭКСТРЕМУМА – она как убывала, так и осталась убывающей.
! Повторим важный момент: точки  не считаются критическими – в них функцияне определена. Соответственно, здесь экстремумов не может быть в принципе (даже если производная меняет знак).
не считаются критическими – в них функцияне определена. Соответственно, здесь экстремумов не может быть в принципе (даже если производная меняет знак).
Ответ: функция возрастает на  и убывает на
и убывает на  В точке
В точке  достигается максимум функции:
достигается максимум функции: 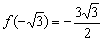 , а в точке
, а в точке 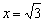 – минимум:
– минимум:  .
.
Знание интервалов монотонности и экстремумов вкупе с установленными асимптотамидаёт уже очень хорошее представление о внешнем виде графика функции. Человек среднего уровня подготовки способен устно определить, что у графика функции 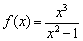 есть две вертикальные асимптоты
есть две вертикальные асимптоты  и наклонная асимптота
и наклонная асимптота  . Вот наш герой:
. Вот наш герой:
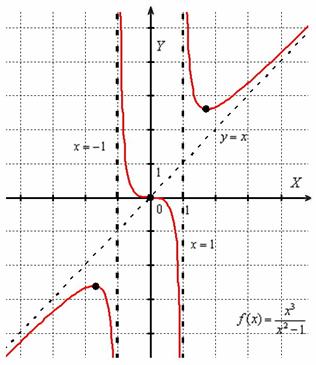
Постарайтесь ещё раз соотнести результаты исследования с графиком данной функции.
В критической точке 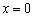 экстремума нет, но существует перегиб графика (что, как правило, и бывает в похожих случаях).
экстремума нет, но существует перегиб графика (что, как правило, и бывает в похожих случаях).