 |
|
Как найти интервалы знакопостоянства функции?
Алгоритм метода интервалов прост и бесхитростен:
1) Находим область определения функции.
2) Находим нули функции (точки пересечения графика с осью абсцисс).
3) В большинстве заданий потребуется чертёж. Чертим ось 
и откладываем на ней точки разрыва (если они есть), а также нули функции (если они есть). Определяем знаки функции на интервалах, которые входят в область определения.
Пункты можете законспектировать, впрочем, алгоритм очень быстро запомнит даже полный чайник. Тут всё прозрачно и логично.
Начнём с распространённой квадратичной функции:
Пример 1
Найти интервалы знакопостоянства функции.
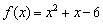
Решение:
1) Функция определена и непрерывна на всей числовой прямой. Таким образом, точки разрыва и «нехорошие» промежутки отсутствуют.
2) Найдём нули функции. Для этого нужно решить уравнение 
. В данном случае:
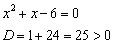
Дискриминант положителен, значит, уравнение имеет два действительных корня:
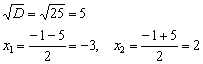
3) Откладываем все найденные точки на числовой оси:
В статье Область определения функции я выполнял подобные чертежи схематически, но сейчас для бОльшей наглядности изложения буду их масштабировать (за исключением клинических случаев). На том же уроке мы узнали, как выяснить знаки функции на интервалах – можно проанализировать расположение параболы. В данном случае ветви параболы направлены вверх, следовательно, на интервалах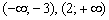 
функция будет положительна: 
. Попа параболы сидит на интервале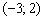 
ниже оси абсцисс, и функция здесь отрицательна: 
.
Хорошо, параболу многие читатели представляют. Но что делать, если функция более сложная? Например,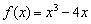 
. Заметная часть аудитории уже затруднится сказать, как принципиально выглядит график данной функции. И это, так скажем, ещё только минимальное усложнение.
Однако и в простых и в сложных случаях работает универсальный способ:
Рассмотрим функцию 
непрерывную на некотором интервале 
, график которой не пересекает ось на этом интервале. Тогда:
– если функция положительна в какой-либо точке интервала , то она положительна и ВО ВСЕХ точках данного интервала;
– если функция отрицательна в какой-либо точке интервала , то она отрицательна и ВО ВСЕХ точках данного интервала.
Включите немного воображения: если на интервале нет точек разрыва, и график не пересекает ось абсцисс, то он не может по мановению волшебной палочки перескочить из нижней полуплоскости в верхнюю полуплоскость (или наоборот). Поэтому знак функции на таком интервале легко определить по одной-единственной точке.
Проведём небольшой эксперимент. Представьте, что вы совсем не знаете, как выглядит график функции 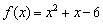и вам необходимо найти её интервалы знакопостоянства (кстати, если действительно не знаете, таки начертите многострадальную примадонну =)).
1) Берём произвольную точку интервала 
. С вычислительной точки зрения проще всего взять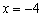 
. Подставляем её в нашу функцию:
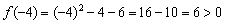
Следовательно, функция положительна ив каждой точке интервала .
2) Берём произвольную точку интервала 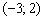, здесь по удобству вне конкуренции ноль. Снова выполняем подстановку:
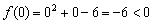
А, значит, функция отрицательна ив каждой точке интервала .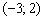
3) И, наконец, обрабатываем наиболее простую точку интервала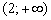 
:
Поэтому функция положительна в каждой точке интервала .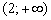
Выполненные подстановки, вычисления почти всегда нетрудно выполнить устно, но в крайнем случае существует и черновик.
Фиксируем полученные результаты на числовой оси:
Да, вы не имеете никаких представлений о параболе, но совершенно точно можете сказать, что на интервалах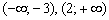 
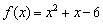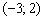график функции расположен ВЫШЕ оси , а на интервале – НИЖЕ данной оси.
Ответ:
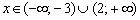, если 
;
, если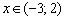 
.
Точно так же решается целый спектр задач-«сателлитов», вот некоторые из них:
Решить квадратичное неравенство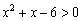 
.
Проводим аналогичные действия и даём ответ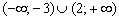 
.
Решить квадратичное неравенство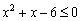 
.
Проводим аналогичные действия и даём ответ 
.
Найти область определения функции 
.
Проводим аналогичные действия, даём ответ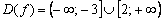 
.
И т.п.
Метод интервалов работает в самых примитивных случаях, например, для функции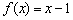 
. Здесь прямая пересекает ось абсцисс в точке 
, при этом слева от данной точки (график ниже оси ), а справа (график выше оси ). Тем не менее, для тех, кто в танке, задача разрешима и методом интервалов.
Может ли функция быть положительно или отрицательной на всей числовой прямой? Конечно, в статье Область определения функции мы рассмотрели типовые примеры. В частности выяснили, что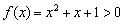 
(парабола, полностью лежащая в верхней полуплоскости). Метод интервалов проходит и тут! Рассматриваем единственный интервал 
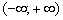, берём из него самую удобную точку 
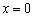и выполняем подстановку: 
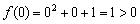. А значит, функция положительна и в каждой точке интервала .
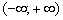Перейдём к кубическим многочленам:
Пример 2
Найти интервалы знакопостоянства функции.
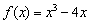
Решение: снова придерживаемся алгоритма:
1) Функция определена на всей числовой прямой.
2) Найдём нули функции, то есть решим уравнение . Для этого выполним разложение на множители:
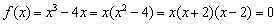
Таким образом, нули функции: 
.
3) Откладываем найденные значения на числовой прямой:
Теперь в каждом из 4-х полученных интервалов берём наиболее простую точку и находим значения функции в данных точках:
Таким образом:
Ответ:
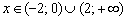, если 
;
, если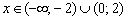 
.
Вы можете не знать, как выглядит график функции 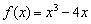, но уже, по крайне мере, понятно, где он выше оси , а где ниже.
Кубическая функция настолько распространена, что не удержусь от полного чертежа «молнии»:
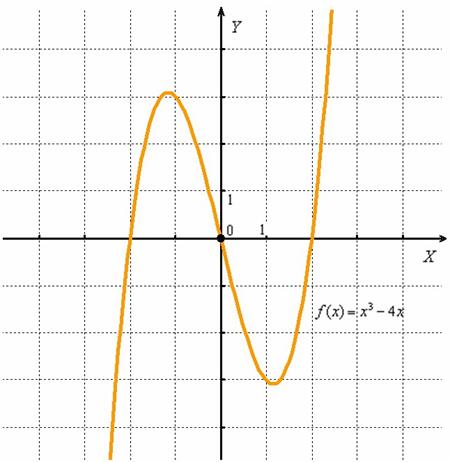
Казалось бы, решение можно упростить: взять левый интервал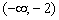 
, выяснить, что на нём функция отрицательна, а дальше знаки будут чередоваться – «плюс», «минус», «плюс». Знакочередование бывает часто, но…