 |
|
Выпуклость, вогнутость и точки перегиба графика
Рассмотрим график функции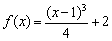 
, которая непрерывна на всей числовой прямой:
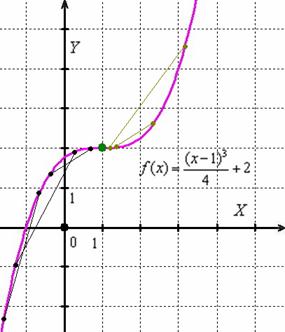
Его легко построить с помощью геометрических преобразований, и, наверное, многие читатели в курсе, как он получен из кубической параболы.
Назовём хордой отрезок, соединяющий две различные точки графика.
График функции является выпуклым на некотором интервале, если он расположен не ниже любой хорды данного интервала. Подопытная линия выпукла на 
, и, очевидно, что здесь любая часть графика расположена НАД своей хордой. Иллюстрируя определение, я провёл три чёрных отрезка.
График функции являются вогнутым на интервале, если он расположен не выше любой хорды этого интервала. В рассматриваемом примере пациент вогнут на промежутке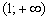 
. Пара коричневых отрезков убедительно демонстрирует, что тут и любой кусок графика расположен ПОД своей хордой.
Точка графика, в которой он меняет выпуклость на вогнутость или вогнутость на выпуклость, называется точкой перегиба. У нас она в единственном экземпляре (первый случай), причём, на практике под точкой перегиба можно подразумевать как зелёную точку 
, принадлежащую самой линии, так и «иксовое» значение 
.
ВАЖНО! Перегибы графика следует изображать аккуратно и очень плавно. Недопустимы всевозможные «неровности» и «шероховатости». Дело за небольшой тренировкой.
Второй подход к определению выпуклости/вогнутости в теории даётся через касательные:
Выпуклый на интервале график расположен не выше касательной, проведённой к нему в произвольной точке данного интервала. Вогнутый же на интервале график – не нижелюбой касательной на этом интервале.
Гипербола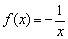 
вогнута на интервале 
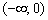и выпукла на 
:
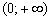При переходе через начало координат вогнутость меняется на выпуклость, однако точку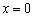 
НЕ СЧИТАЮТ точкой перегиба, так как функция 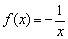не определена в ней.
Более строгие утверждения и теоремы по теме можно найти в учебнике, а мы переходим к насыщенной практической части:
Как найти интервалы выпуклости, интервалы вогнутости
и точки перегиба графика?
Материал прост, трафаретен и структурно повторяет исследование функции на экстремум.
Выпуклость/вогнутость графика характеризует вторая производная функции.
Пусть функция 
дважды дифференцируема на некотором интервале. Тогда:
– если вторая производная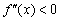 
на интервале, то график функции 
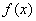является выпуклым на данном интервале;
– если вторая производная 
на интервале, то график функции 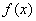является вогнутым на данном интервале.
На счёт знаков второй производной по просторам учебных заведений гуляет доисторическая ассоциация: «–» показывает, что «в график функции нельзя налить воду» (выпуклость),
а «+» – «даёт такую возможность» (вогнутость).