 |
|
ГЛАВА 1. ЧИСЛОВЫЕ ФУНКЦИИ НА ЛИНЕЙНЫХ ПРОСТРАНСТВАХ
Рассмотрим некоторые полезные функции одной и двух переменных, заданные на линейном пространстве над произвольным полем и принимающие значения в этом поле (их называют числовыми функциями).
§1. Линейные функции
Определение 1. Линейное отображение 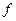 линейного пространства
линейного пространства  над полем
над полем  в
в  называют линейной функцией, или линейной формой, заданной на
называют линейной функцией, или линейной формой, заданной на  .
.
Примером линейной функции является функция 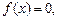 заданная на любом линейном пространстве над полем
заданная на любом линейном пространстве над полем  .
.
Нетрудно получить общий вид линейной функции, заданной на произвольном конечномерном линейном пространстве.
Теорема 1.Пусть 
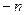 - мерное линейное пространство над
- мерное линейное пространство над  ,
,  – линейная функция на
– линейная функция на  и
и 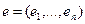 – произвольный базис
– произвольный базис  . Тогда в этом базисе функция
. Тогда в этом базисе функция 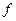 запишется так:
запишется так:
 , (1)
, (1)
где  – координатный столбец вектора
– координатный столбец вектора 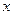 в базисе
в базисе  ,
, 

Доказательство.Пусть 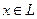 . Так как
. Так как  – базис
– базис  , то
, то  . По определению линейной функции отсюда получаем:
. По определению линейной функции отсюда получаем: 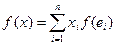 . Введём обозначения:
. Введём обозначения: 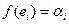 ,
,  Получаем:
Получаем:
 , где
, где 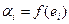 ,
, 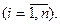
Теорема доказана.
Нетрудно проверить, что множество  всех линейных функций, заданных на линейном пространстве
всех линейных функций, заданных на линейном пространстве  над полем
над полем  , также является линейным пространством над
, также является линейным пространством над  . Его называют сопряженным (или двойственным) к
. Его называют сопряженным (или двойственным) к  .
.
Подробнее об  и его связях с
и его связях с  можно прочитать в [3].
можно прочитать в [3].
Замечание. В записи (1) 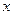 – переменный вектор из
– переменный вектор из  ,
, 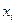 – переменные, принимающие значения в поле
– переменные, принимающие значения в поле  .
.
§2. Билинейные функции
Рассмотрим теперь числовую функцию двух переменных, заданную на линейном пространстве.
Определение 2.Пусть  – линейное пространство над
– линейное пространство над  . Функция двух переменных
. Функция двух переменных  , заданная на
, заданная на  и принимающая значения в поле
и принимающая значения в поле  , называется билинейной функцией (или билинейной формой), если она линейна по каждому аргументу, т.е.
, называется билинейной функцией (или билинейной формой), если она линейна по каждому аргументу, т.е.  и
и  справедливы равенства:
справедливы равенства:
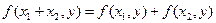 ;
;

(линейность по 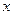 при неизменном
при неизменном 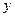 ) и аналогичная линейность по
) и аналогичная линейность по 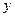 при неизменном
при неизменном 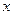 .
.
Билинейную функцию также можно записать в координатах, если  – конечномерное линейное пространство над
– конечномерное линейное пространство над  .
.
Пусть  – некоторый базис
– некоторый базис  ,
,  Тогда
Тогда  ,
,  .
.
Учитывая определение билинейной функции, получаем:  . (2)
. (2)
Введем обозначения: 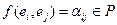 . Тогда из (2) получим:
. Тогда из (2) получим:
 (3) – запись билинейной функции в координатах ( т.е. в некотором базисе пространства
(3) – запись билинейной функции в координатах ( т.е. в некотором базисе пространства  ).
).
Определение 3. Матрица  из элементов
из элементов  , входящих в запись (3), называется матрицей билинейной функции
, входящих в запись (3), называется матрицей билинейной функции 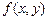 .
.
Определение 4.Если 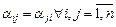 (4), то билинейную функцию
(4), то билинейную функцию  вида (3) называют симметричной.
вида (3) называют симметричной.
Пример. Рассмотрим скалярное произведение  векторов-отрезков на плоскости. Легко проверить, что это – симметричная билинейная форма.
векторов-отрезков на плоскости. Легко проверить, что это – симметричная билинейная форма.
§3. Квадратичные формы
Определение 5.Пусть  – симметричная билинейная функция на линейном пространстве
– симметричная билинейная функция на линейном пространстве  . Если положить
. Если положить  , то числовая функция
, то числовая функция  одной переменной называется квадратичной формой.
одной переменной называется квадратичной формой.
Пример. Рассмотрим на пространстве векторов-отрезков скалярный квадрат вектора 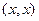 . Нетрудно убедиться, что это – квадратичная форма.
. Нетрудно убедиться, что это – квадратичная форма.
Из определения квадратичной формы и вида (3) билинейной формы следует, что
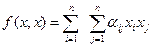 . (5)
. (5)
Мы получили вид квадратичной формы, заданной на конечномерном линейном пространстве, в некотором базисе этого пространства.
Матрица  называется матрицей квадратичной формы
называется матрицей квадратичной формы  .
.
Заметим, что в силу определений 4 и 5 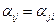 или
или  , т.е. матрица квадратичной формы симметрична относительно главной диагонали (такую матрицу называют симметрической).
, т.е. матрица квадратичной формы симметрична относительно главной диагонали (такую матрицу называют симметрической).
Ниже мы будем рассматривать квадратичные формы в основном на конечномерных линейных пространствах.
Замечание 1. На квадратичную форму (5) можно смотреть также как на многочлен вида (5) от 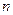 переменных
переменных  над
над  , все члены которого – степени 2. Тогда её обозначают через
, все члены которого – степени 2. Тогда её обозначают через  . Отметим, что неизвестные мы считаем перестановочными.
. Отметим, что неизвестные мы считаем перестановочными.
Введем обозначение:  . Тогда
. Тогда 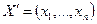 . Пусть
. Пусть  – матрица квадратичной формы (5).
– матрица квадратичной формы (5).
Рассмотрим  . Умножив это равенство слева на
. Умножив это равенство слева на  , получим
, получим
 .
.
Мы показали:
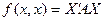 (6). Это матричная запись квадратичной формы
(6). Это матричная запись квадратичной формы  .
.
Легко проверить справедливость следующего утверждения:
Лемма. Пусть 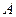 и
и 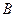 – две матрицы и существует
– две матрицы и существует  . Тогда
. Тогда  .
.
Замечание 2. Индукцией отсюда получаем 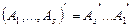 .
.