Главная | Обратная связь

Приведение квадратичной формы к каноническому виду

 

Определение 6. Пусть 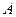– матрица квадратичной формы в некотором базисе конечномерного линейного пространства . Тогда ранг матрицы 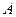называется рангом квадратичной формы .

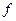Покажем, что это определение не зависит от выбора базиса.

Теорема 3.При невырожденном линейном преобразовании неизвестных ранг квадратичной формы не меняется.

Доказательство. Если квадратичная форма с матрицей 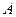подвергается преобразованию , то по теореме 2 получится квадратичная форма с матрицей . Но, как известно, при умножении матрицы на любую невырожденную матрицу ранг не меняется, и потому .

Теорема доказана.

Замечание 4.На языке линейных пространств теорема 3 формулируется следующим образом.

Теорема 3^’.Если квадратичная форма задана на конечномерном линейном пространстве , то в любом базисе этого пространства имеет один и тот же ранг.

Определение 7. Если (10) в некотором базисе 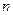– мерного линейного пространства над , где , , то говорят, что (10) – её канонический вид.

Отметим, что в каноническом виде квадратичная форма имеет диагональную матрицу

.

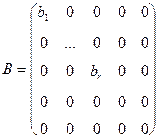Если в матрице 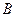, , то – ранг квадратичной формы .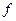

Мы видим, что число квадратов с отличными от нуля коэффициентами в каноническом виде квадратичной формы равно её рангу.

Теорема 4(о приведении к каноническому виду). Пусть – квадратичная форма на конечномерном линейном пространстве над и характеристика поля отлична от 2.

Тогда существует базис пространства , в котором имеет канонический вид (такой базис называют каноническим базисом). (Другими словами: с помощью невырожденного линейного преобразования неизвестных любую квадратичную форму над таким полем можно привести к каноническому виду).

Доказательство.Будем рассматривать как многочлен от :

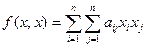. (5)

Возможны 2 случая.

. (т.е. в 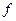нет квадратов с ненулевыми коэффициентами).

Если , то это канонический вид,

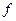Пусть , например . Тогда (11) (мы выделили в все члены, содержащие ).

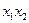Образуем два квадрата, совершив следующее линейное преобразование неизвестных:

(12)

 

 

Его матрица

.

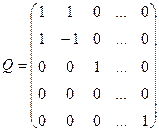Разлагая по первым двум строкам, получаем: , так как характеристика поля по условию теоремы не равна 2.

Значит, (12) – невырожденное линейное преобразование неизвестных. После него квадратичная форма из вида (11) перейдет в вид (13), причем в силу (12) в будут входить только слагаемые, содержащие произведения , где или , или больше двух, поэтому и не появятся в и не могут сократиться в (13).

Итак, в виде (13) появляются два квадрата неизвестных с ненулевыми коэффициентами.

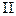. В существует квадрат с ненулевым коэффициентом. Можно считать, что . (14)

Основная идея доказательства: собираем в 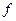все члены с и дополняем эту сумму до полного квадрата. Получится , где ­– некоторая линейная функция.

Реализовать эту идею можно так. Хорошо известна формула

.

Из квадратичной формы 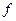вычтем следующее выражение, подобранное так, чтобы сократились все члены, содержащие :

(14)

(здесь – квадратичная форма, не содержащая ) .

Мы получили

. (15)

Совершим теперь следующее линейное преобразование неизвестных:

 

(16)

Так как , то это преобразование невырожденное. После него из (15) получим

(17) (говорят, что выделился квадрат неизвестного ).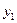

То же самое проделываем далее для квадратичной формы 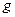, т.е. выделяем квадрат ещё одного неизвестного (если квадратов в 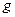нет, предварительно их образуем, как в пункте ). При этом к линейному преобразованию неизвестных дописываем равенство 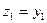(переобозначаем 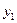). Так как неизвестных конечное число, то через конечное число шагов получим

(18) – канонический вид квадратичной формы .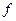

Так как последовательное выполнение нескольких невырожденных линейных преобразований можно заменить одним – их произведением (его матрица – произведение матриц сомножителей) и оно тоже будет невырожденным, то теорема доказана.

Замечание 5. Канонический вид квадратичной формы не единственен. Действительно, если в каноническом виде (18) совершить следующее линейное невырожденное преобразование неизвестных.

(19)

где , , получим

. (20)

Вообще говоря, (20) – это другой канонический вид квадратичной формы .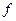

Отметим, что во всех канонических видах квадратичной формы 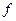по теореме 3 один и тот же ранг , т.е. одинаковое число квадратов с ненулевыми коэффициентами.