 |
|
Комплексный нормальный вид
Рассмотрим квадратичные формы над полем С комплексных чисел.
Из канонических видов (20) такой квадратичной формы можно выбрать наиболее простой: для этого возьмем в (19) числа  такими, чтобы
такими, чтобы 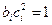 , т.е.
, т.е.  (21). Тогда после линейного преобразования (19) с этими (комплексными) коэффициентами вид (20) будет таким:
(21). Тогда после линейного преобразования (19) с этими (комплексными) коэффициентами вид (20) будет таким:
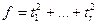 (22) . Такой канонический вид называют комплексным нормальным видом, или нормальным видом над
(22) . Такой канонический вид называют комплексным нормальным видом, или нормальным видом над  .
.
Он определяется только рангом квадратичной формы 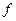 . Это канонический вид, в котором все квадраты входят с коэффициентом либо +1, либо 0.
. Это канонический вид, в котором все квадраты входят с коэффициентом либо +1, либо 0.
Действительный нормальный вид
Рассмотрим квадратичную форму 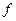 над полем
над полем  действительных чисел и её канонические виды (20):
действительных чисел и её канонические виды (20):  . Коэффициенты в (20) действительные.
. Коэффициенты в (20) действительные.
Как получить “наиболее простой” из этих действительных канонических видов?
Формулы (21) нам не помогут, если  , ибо здесь мы имеем право совершать линейные преобразования только с действительными коэффициентами.
, ибо здесь мы имеем право совершать линейные преобразования только с действительными коэффициентами.
Совершим линейное преобразование (19) с действительными коэффициентами 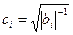 (23), ,
(23), ,  ,
,  Тогда (20) имеет следующий вид:
Тогда (20) имеет следующий вид:
 (24) , где
(24) , где  (25).
(25). 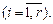
Этот канонический вид называют действительным нормальным видом, или нормальным видом над полем  .
.
С точностью до нумерации неизвестных его можно записать так:  (26).
(26).
§5. Закон инерции действительных квадратичных форм
Естественно возникает вопрос: сколько действительных нормальных видов (ДНВ) может быть у действительной квадратичной формы?
Теорема 5.Если квадратичная форма  в двух базисах действительного линейного пространства
в двух базисах действительного линейного пространства  имеет действительные нормальные виды (26) и
имеет действительные нормальные виды (26) и  (27), то
(27), то  (28).
(28).
Доказательство. Предположим противное. Не нарушая общности, можно считать, что 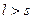 (29). Пусть
(29). Пусть 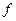 имеет ДНВ (26) в базисе
имеет ДНВ (26) в базисе 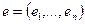 , а ДНВ (27) – в базисе
, а ДНВ (27) – в базисе  .
.
Рассмотрим следующие два подпространства: линейную оболочку 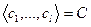 (30) и линейную оболочку
(30) и линейную оболочку  . (31) Тогда
. (31) Тогда  (32) (ибо
(32) (ибо  – базис
– базис  ), а
), а 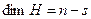 (33) (в силу (31)).
(33) (в силу (31)).
Рассмотрим сумму 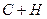 . Имеем:
. Имеем:

 (34).
(34).
Но 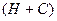 – подпространство линейного пространства
– подпространство линейного пространства  , поэтому
, поэтому  . Отсюда и из (34) получаем:
. Отсюда и из (34) получаем:  . Отсюда и из неравенства (29) получаем:
. Отсюда и из неравенства (29) получаем:  , т.е.
, т.е.  . Значит,
. Значит,  . Так как
. Так как 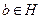 , то из (31) следует:
, то из (31) следует: 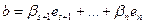 (35). Если теперь в ДНВ (26) подставить координаты вектора
(35). Если теперь в ДНВ (26) подставить координаты вектора  , то получим:
, то получим:  , т.е.
, т.е. 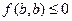 (36) (равенство нулю возможно, если, например, только
(36) (равенство нулю возможно, если, например, только 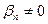 ).
).
С другой стороны, из 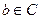 следует:
следует:  (37), где
(37), где 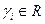 ,
, 
Отметим, что  , и поэтому
, и поэтому 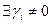 . Подставив координаты вектора
. Подставив координаты вектора  в (27), получим:
в (27), получим:  (38) .
(38) .
Неравенство (38) противоречит неравенству (36). Значит, наше предположение 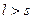 ложно. Аналогично ложно и
ложно. Аналогично ложно и 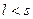 . Таким образом ,
. Таким образом ,  .
.
Теорема доказана.
Определение 8. Число положительных квадратов в действительном нормальном виде действительной квадратичной формы 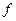 называется положительным индексом инерции
называется положительным индексом инерции  , число отрицательных квадратов – отрицательным индексом инерции
, число отрицательных квадратов – отрицательным индексом инерции  . Разность
. Разность  называется сигнатурой квадратичной формы
называется сигнатурой квадратичной формы 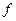 .
.
Замечание 6.Закон инерции означает единственность действительного нормального вида с точностью до обозначений.
Нетрудно доказать следующее:
Утверждение. Если 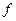 и
и 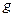 – две действительные квадратичные формы, то одну из них можно перевести в другую с помощью невырожденного линейного преобразования неизвестных тогда и только тогда, когда они имеют один и тот же действительный нормальный вид.
– две действительные квадратичные формы, то одну из них можно перевести в другую с помощью невырожденного линейного преобразования неизвестных тогда и только тогда, когда они имеют один и тот же действительный нормальный вид.
Доказательство.
Если  , то
, то  . И наоборот, если
. И наоборот, если 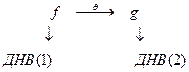 , то ДНВ(1) и ДНВ(2) – два действительных нормальных вида
, то ДНВ(1) и ДНВ(2) – два действительных нормальных вида 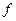 и по закону инерции они совпадают.
и по закону инерции они совпадают.
Утверждение доказано.