 |
|
Положительно определенные квадратичные формы
Определение 9.Квадратичная форма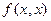 
, заданная на действительном линейном пространстве 
, называется положительно определенной, если 
для любого 
.
Теорема 6. Действительная квадратичная форм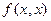а на 
-мерном линейном пространстве положительно определенная тогда и только тогда, когда её действительный нормальный вид таков:
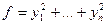(39) (т.е. в нем нет квадратов с коэффициентами 0 и –1; другими словами, ранг 
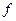и её положительный индекс равны 
).
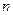Необходимость.Пусть 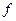– положительно определенная квадратичная форма. Будем доказывать от противного: пусть в её ДНВ существует квадрат 
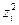с коэффициентом (–1) или 0. Тогда
(40) либо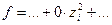 
(41)
(виды (40) и (41) – в некотором базисе линейного пространства ).
Рассмотрим вектор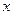 
, у которого координаты в этом базисе таковы: 
, а остальные равны 0, т.е.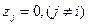 
: 
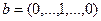. Тогда в силу (40) и (41) либо 
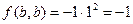, либо 
, т.е.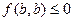 
, что вступает в противоречие с определением положительно определенной квадратичной формы (ибо 
). Значит, 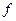имеет ДНВ (39).
Достаточность.Пусть (39) – действительный нормальный вид 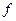в некотором базисе 
. Тогда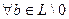 
с координатным столбцом 
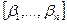в этом базисе имеем: 
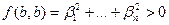(ибо 
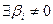). Значит, 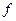– положительно определенная квадратичная форма.
Замечание 7. С помощью этой теоремы не очень удобно определять, будет ли 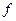положительно определенной (надо приводить её к ДНВ).
Есть более удобный способ.
Определение 10. Пусть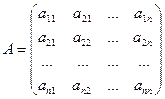 
– некоторая квадратная матрица. Её миноры 1-го, 2-го,…, 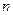-го порядка, расположенные в левом верхнем углу, называются главными минорами матрицы 
.
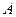Если 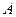– матрица квадратичной формы 
, то главные миноры матрицы 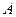называются главными минорами .
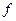Теорема(критерий Сильвестра).Действительная квадратичная форма является положительно определенной тогда и только тогда, когда все её главные миноры больше нуля.
Доказательство этой теоремы можно найти в любом учебнике линейной алгебры. Здесь мы его не приводим.
Определение 11.Квадратичная форма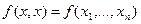 
, заданная на линейном пространстве , называется отрицательно определенной, если 
.
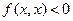Если 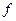отрицательно определенная форма, то, очевидно, 
– положительно определенная квадратичная форма, т.е.
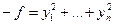– действительный нормальный вид , а тогда 
– действительный нормальный вид отрицательно определенной квадратичной формы .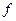
В матрице отрицательно определённой квадратичной формы, как нетрудно видеть, знаки главных миноров чередуются.
ГЛАВА 2. ЕВКЛИДОВЫ ПРОСТРАНСТВА