Главная | Обратная связь

Ортогональные системы векторов

Определение 1. Два вектора a и b евклидова пространства V называются ортогональными, если (a, b)=0.

Легко проверяется, что (0, b)=0: (0, b)= (0a, b)= 0(a, b)=0.

Определение 2. Система векторов а₁,…,а_s (1) евклидова пространства V называется ортогональной, если любые ее векторы ортогональны, т.е. (а_i, a_j)=0 (2) для любых i, j при i j (i, j=1,...,s)

Теорема 1.Всякая ортогональная система (1) ненулевых векторов линейно независима.

Доказательство. Пусть дана система векторов (1) с условием (2). Составим уравнение, где x₁, ..., x_s – неизвестные числа: x₁a₁+...+x_ia_i+...+x_sa_s=0 (3). Умножая равенство (3) скалярно на вектор a_i, получим: x₁(a₁,a_i)+...+
x_i (a_i,a_i)+...+x_s (a_s,a_i)= (0,a_i)= 0. Отсюда и из (2) следует: x_i (a_i,a_i)= 0 (4). Так как a_i 0, то (a_i,a_i) 0; поэтому из (4) получаем: x_i=0. Мы показали, что уравнение (3) имеет только нулевое решение. Значит, система (1) линейно независима.

Теорема доказана.

Один способ построения ортогональных систем ненулевых векторов приводится ниже в теореме 2.

Теорема 2.Пусть в евклидовом пространстве V задана линейно независимая система a₁,...,a_s (5). Тогда в V существует ортогональная система b₁,...,b_s (6), удовлетворяющая условиям:

1. b₁= a₁;

2. b_k Î <a₁,a₂,...,a_k>;

3. b_k 0 для любого k=1,…,s.

Доказательство. Будем доказывать эту теорему индукцией по числу s. При s=1 она верна: полагаем b₁= a₁. Предположим, что уже построена система b₁,...,b_i-1 (7), удовлетворяющая условиям 1, 2, 3 при k≤ i-1, и векторы (7) попарно ортогональны. Вектор b_i будем искать в виде b_i= a_i+a₁b₁+...+a_i-1b_i-1 (8), где a_j – неизвестные числа. Мы найдем их из условий (b_i, b_j)=0 (9) для любого j=1,…,i-1. Для нахождения a_j равенство (8) умножим скалярно на b_j: (b_i, b_j)=0=( a_i, b_j)+ a₁(b₁, b_j)+...+ a_j(b_j, b_j)+...+ a_i-1(b_i-1, b_j). Ввиду условий (9) из этого равенства получаем: 0= ( a_i, b_j) + a_j(b_j, b_j), откуда 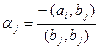(10) (отметим, что (b_j, b_j)≠0, ибо b_j≠0 по предположению индукции). Если числа a_j из (10) подставить в (8), то мы получим вектор b_i , ортогональный всем векторам системы (7), т.е. система b₁,...,b_i-1,b_i (11) будет ортогональной.

Отметим, что ввиду предположения индукции {b₁,...,b_i-1}Î <a₁,...,a_i-1> (12); поэтому каждый из векторов (7) линейно выражается через векторы a₁,...,a_i-1. Подставляя эти выражения в (8), мы получим: b_i= a_i+j₁a₁+...+j_i-1a_i-1 (13). Это означает, что выполняется условие 2 для b_i. Если бы b_i =0, то из (13) следовало бы, что система (1) линейно зависима, что противоречит условию.

Итак, мы построили такой вектор b_i, что система (11) удовлетворяет всем требованиям теоремы для i векторов (i £ s). Такое построение можно продолжать до тех пор, пока не используются все векторы системы (5), т.е. получаем ортогональную систему ненулевых векторов (6), удовлетворяющую условиям 1 – 3.

Теорема доказана.

Определение 3.Переход от линейно независимой системы (5) к построенной выше ортогональной системе (6) называется процессом ортогонализации.

Определение 4.Базис a₁,...,a_n n-мерного евклидова пространства V_n называется ортогональным базисом, если он является ортогональной системой.

Из теорем 1 и 2 вытекает справедливость следующих утверждений.

Следствие 1.Во всяком конечномерном евклидовом пространстве V_n существует ортогональный базис.

Доказательство. По условию в V_n существует базис a₁,...,a_n (14). С помощью процесса ортогонализации из него можно получить ортогональную систему из n ненулевых векторов b₁,...,b_n (15). По теореме 1 она линейно независима. Так как число ее векторов равно dim V_n, то (15) – базис V_n.

Это искомый ортогональный базис.

Следствие 2.Всякий ненулевой вектор евклидова пространства V_n при n³2 содержится в некотором ортогональном базисе этого пространства. Для доказательства дополняем этот вектор до базиса V_n и подвергаем этот базис процессу ортогонализации.