 |
|
За методом Клемана-Дезорма
Мета роботи:зрозуміти газові закони та перший закон термодинаміки, ознайомитися з методами визначення відношення теплоємності газу при сталому тиску до його теплоємності при сталому об’ємі, виміряти відношення теплоємкостей для повітря.
Теплоємністю тіла називають кількість тепла, яку треба надати йому чи відібрати для зміни температури тіла на один градус:
.
Розглядають питому cта молярну CM теплоємності, які характеризують вже не тіло, а речовину, з якої складається тіло. Молярна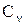 
теплоємність (теплоємність одного моля):
.
Питома с теплоємність (теплоємність одиниці маси):
.
Зв’язок між молярною Сm і питомою теплоємностями: 
.
Однак, за першим законом термодинаміки, отримане тілом тепло dQвитрачається не тільки на збільшення внутрішньої енергії dU, а й на виконання тілом роботи dA:
.
Тому, залежно від того, здійснюється чи ні робота при нагріванні тіла, до нього треба підвести більшу чи меншу кількість тепла для однієї й тієї ж зміни його внутрішньої енергії(температури). Таким чином, теплоємність визначається не тільки властивостями речовини, але залежить також від умов нагрівання тіл та є функцією процесу.
Для твердих та рідких тіл робота, яка пропорційна зміні об’єму dV тіла при його нагріванні 
, дуже мала, що їй можна знехтувати, тому теплоємність цих тіл в різних процесах практично однакова. Це пов’язано з тим, що такі тіла мають малі значення температурного коефіцієнту розширення.
Для газів залежність величини теплоємності від виду процесу виявляється суттєвою. Якщо нагрівання газу відбувається без здійснення роботи, тобто при сталому об’ємі, то відповідна цьому процесу теплоємність має назву теплоємності при сталому об’ємі Cvта ,так як в даному випадку dA=0 та dQ = dU, то
,
а зміна внутрішньої енергії газу dU = CvdT.
Якщо при нагріванні на dT газ здійснює роботу, то для тієї ж зміни внутрішньої енергії треба затратити тепло більше на величину цієї роботи. З урахуванням виразів для dAта dU перший закон термодинаміки треба записати таким чином:
.
Зокрема, при нагріванні зі здійсненням роботи тиск може залишитись сталим. Теплоємність такого процесу має назву теплоємності при сталому тиску Cp і дорівнює
,
тобто більше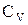 
на величину 
. Останню величину легко обчислити для ідеального газу з рівняння його стану 
. Для 1 молю газу 
газу при сталому тиску (p = const): 
, звідси отримаємо рівняння Майєра:
.
Враховуючи, що внутрішня енергія молю ідеального газу 
, де і – число ступенів свободи , запишемо: 
та 
.
Для опису адіабатичного процесу, а також для великої кількості інших процесів, суттєве значення має відношення 
, яке іноді називають коефіцієнтом Пуассона. Очевидно, що для газів 
. Таким чином, це відношення може бути знайдено шляхом розрахунку, якщо відомо число ступенів свободи i молекули даного газу. Для одноатомних газів i=3, звідки 
, а для двохатомних (N2 ,O2 ) – i=5 та 
.
Для експериментального визначення g можна використати рівняння адіабатичного процесу 
. Один з методів базується на тому, що процес розповсюдження звукових коливань в газах є майже адіабатичним, причому швидкість розповсюдження звуку в повітрі має наступний вираз: 
, звідси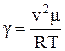 
.
Визначив експериментально швидкість звуку та температуру газу відомого хімічного складу (це означає, що відома молярна маса m), можна знайти величину g.
В методі Клемана-Дезорма (рис. 12) використовують балон, з’єднаний трубкою з водяним манометром та іншою трубкою з краном K, який з’єднує балон об’ємом V з оточуючим повітрям. Цю трубку використовують для накопичення у балоні повітря за допомогою ручного насосу та для випуску надлишку повітря. В методі газ послідовно проходить крізь три стани, які характеризуються такими параметрами (P1 ,V1, T1 ), (P2 ,V, T2 ), (P2 ,V, T1 ).
До балону при закритому крані накачують повітря. Надмірний тиск можна визначити за допомогою відкритого манометру. Так як повітря, що стискається під поршнем насосу, нагрівається, то треба зачекати, поки внаслідок теплообміну температура його зрівняється з температурою оточуючого середовища T1. При цьому тиск повітря P1 в балоні визначається за усталеною різницею рівнів рідини в манометрі. Відкривши кран, ми даємо повітрю можливість виходити з балону, поки тиск у ньому не зрівняється з зовнішнім, атмосферним Р0, після чого кран K знову закриваємо. Зрозуміло, що маса газу, яка тепер заповнює об’єм V балону, займала перед відкриттям крану менший об’єм V1, який був лише частиною повного об’єму V. Процес розширення газу можна вважати адіабатичним, так як він відбувається настільки швидко, що помітного теплообміну між газом та стінками балону не здійснюється. Тому повинно виконуватися рівняння адіабати:
(1).
До моменту закриття крану тиск усередині та зовні об’єму зрівнялись, але газ в балоні охолонув внаслідок адіабатичного процесу. Якщо зачекати, поки газ, завдяки теплообміну, нагріється до початкової температури кімнати, то тиск у балоні підвищиться до якоїсь величини р2, що можна відстежити за показами манометру. Порівнюючи цей останній стан маси газу, який залишився у балоні (P2 ,V,T), з початковим, перед відкриттям крану K (P1,V1,T), ми побачимо, що обидва процеси спостерігаються при сталій температурі і тому в даному випадку можна використати закон Бойля-Маріотта
. (2)
З останніх двох рівнянь можна виключити об’єми, які не змінюються. Для цього треба піднести рівняння (2) до степені g та почленно поділити на рівняння (1).
або 
З останнього рівняння величина g може бути знайдена шляхом логарифмування:
Так як практично тиски p1, p2, p0 мало відрізняються між собою, то різниці логарифмів можна замінити різницями відповідних чисел: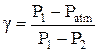 
Різниця рівнів рідини y трубках манометру h показує, на скільки тиск у посудині більше атмосферного, тобто 
, 
. Тому робоча формула для визначення g має вигляд:
,
де h1 – різниця між рівнями рідини в першому стані, h2 – в останньому.