Главная | Обратная связь

Преобразование Лапласа.

Условимся пол р понимать комп­лексное число

p = a + jb, (147)

где а — действительная, jb — мнимая части комплексного числа (в ряде книг вместо буквы р пишут s).

В дальнейшем в соответствии с установившейся практикой коэффи­циент b с учетом знака условимся называть не коэффициентом при мнимой части комплекса (чем он в действительности является), а мнимой частью.

Функцию времени (ток, напряжение, ЭДС, заряд) обозначают f(t) и называют оригиналом. Ей соответствует функция F(p), называ­емая изображением, Для прямого преобразования функций времени f(t) применяется преобразование Лапласа

F(p) .=˙ ∫ f(t) e ^–рt dt (148 )

Знак .=˙ называют знаком соответствия.

Соответствие между функциями F(p) и f(t) записывают так:

F(p) .=˙ f(t) (149 )

где функция времени f(t) - однозначная, называемая оригиналом, определенная при t > 0, интегрируемая в интервале времени 0 ÷ ∞ и равная нулю при t < 0; F(p) — функция комплексного переменно­го р = σ + jω при Rep = σ > 0, называемая лапласовым изображением.

Верхний предел интеграла (148) равен бесконечности. Интегралы с бесконечным верхним пределом называют несобственными. Если в ре­зультате интегрирования и подстановки пределов получают конечное число (не бесконечность), то говорят, что интеграл сходится.

В курсе математики доказывается, что интеграл (148), в состав кото­рого входит функция е ^–рt = е ^–аtе ^-jb, сходится только в том случае, когда модуль функции f(t), если и увеличивается с ростом t, то все же медленнее, чем модуль функции е ^–рt, равный е ^–аt.

Практически все функции f(t), с которыми имеют дело в курсе ТОЭ, этому условию удовлетворяют.

Составим изображения некоторых простейших функций.

5.5. Изображение постоянной.

Требуется найти изображение функции f(t) = А, где А— постоянная величина. С этой целью в (8.3 1) вме­сто f(t) подставим А и проведем интегрирование:

F(p) = _о∫^∞ А е ^–рt dt = А(-1/р) _о∫^∞ d(е ^–рt) t = - (А е ^–рt \р) |^∞_о = А / р ( 150 )

Следовательно, изображение постоянной равно постоянной А, деленной на р.

А .=˙ А/р. (151)

5.6. Изображение показательной функции е ^аt .

Вместо f(t) в (148) подставим е ^аt:

F(p) = _о∫^∞ е ^–аtе ^-рt dt = _о∫^∞ е ^–t(р-а) dt = [-1 /(р- α)] _о∫^∞ е ^–t(р-а) d[-t (р- α)] =

= [-1 /(р-а)] е ^–t(р-а) |^∞_о = [1 /(р-α)] ( 152 )

Таким образом

е ^аt .=˙ [1 /(р- а)] ( 153 )

При выводе формулы (152) (при подстановке пределов) было учте­но, что действительная часть оператора р больше, чем а, т. е. р > α. Только при этом условии интеграл сходится.

Из формулы (8.34) вытекает ряд важных следствий. Положив в ней

α = е ^аt, получим

е ^jωt .=˙ [1 /(р-jω)] (154)

Формула (154) дает возможность найти изображение комплекса си­нусоидального тока:

İ_m e ^j(ωt+ψ) = İ_m e ^jωt

С этой целью обе части (154) умножим на постоянное число İ_m :

İ_m e ^jωt .=˙ İ_m[1 /(р-jω)] ( 155 )

Аналогично, изображение комплекса синусоидального напряжения

U_m e ^jωt .=˙ U_m [1 /(р-jω)] ( 156 )

Функции е ^–аt соответствует изображение 1/(р + α):

е ^–аt .=˙ 1/(р + α) ( 157 )

В таблице 5 приведены примеры изображения простых функций.

Таблица 5. Изображение функций по Лапласу

 

§ 5.7. Изображение первой производной. Известно, что функции f(t), соответствует изображение F(p). Требуется найти изображение первой производной d[f(t)] /dt, если известно, что значение функции f(t), при t = 0 равно f(0) .

Подвергнем функцию df(t)/dt преобразованию Лапласа:

_о∫^∞ [df(t)/dt] е ^-рtdt = _о∫^∞ е ^–рt d[f(t )] ( 158 )

Интегрирование произведем по частям ∫ и dv = иv - ∫ vdu. Обозначив е ^–рt = u и df(t) / dt = dv, получим

_о∫^∞ е ^–рt d[f(t )] = е ^–рt f(t )^∞_о - _о∫^∞ f(t ) d( е ^–рt) ( 159 )

Но

е ^–рt f(t )^∞_о = 0 - f(0) = - f(0) ( 160 )

второе слагаемое _о∫^∞ f(t ) d( е ^–рt)= р _о∫^∞ f(t ) е ^–рt dt = р F(p)

Таким образом,

_о∫^∞ [df(t)/dt] е ^-рtdt = pF(p) - f(0), (161)

или

df(t)/dt .=˙ pF(p)-f(0). (162)

5.8. Изображение второй производной.

Без вывода дадим фор­мулу

d²[f(t)] /dt² .=˙ р² F(p) - р f(0) - df(t)/dt│_t=0 ( 163 )

Следовательно, изображение второй производной тока

d²i /dt² .=˙ р² i (p) - р i(0) - i^’(0) ( 164 )

5.9. Изображение интеграла. Требуется найти изображение фун­кции

_о∫^t f(t)dt, если известно, что изображение функции f(t) равно F(р).

Подвергнем функцию _о∫^t f(t)dt преобразованию Лапласа:

_о∫^∞ {_о∫^t f(t)dt } е ^-рtdt = -(1/р) _о∫^∞ {_о∫^t f(t)dt }dе ^-рt ( 165 )

Примем _о∫^t f(t)dt = и; d( е ^-pl) = dv и возьмем интеграл по частям:

-(1/р)_о∫^∞ {_о∫^t f(t)dt }dе ^-рt = -(1/р) {_о∫^t f(t)dt } е ^-рt |_о^∞ + (1/р) _о∫^∞ f(t) е ^-рt dt= F(p)/ p

Первое слагаемое правой части при подстановке верхнего и нижнего пределов обращается в нуль. При подстановке верхнего предела нуль получается за счет ранее наложенного ограничения на функцию f(t). Функция f(t), если и растет с увеличением t, то все же мед­леннее, чем растет функция е^αt, где α — действительная часть р. При подстановке нижнего предела нуль получим за счет обращения в нуль _о∫^t f(t)dt . Следовательно, если f(t) .=˙ F(p), то

_о∫^t f(t)dt .=˙ F(p) / р ( 166 )

Преобразование (166) позволяет получить соотношения~между напряжением u(t) = и и током i(t) = i в операторной форме для резистивного, индуктивного и емкостного элементов.

Изображение напряжения на резистивном элементе u_r(t) = ri(t) равно

U_r(р) = r _о∫^∞ е ^–рt i(t) dt = r i(p) (167)

 

Рис.29. Схема замещения в операторной форме.

5.10. Изображение напряжения на индуктивном элементе.

Изоб­ражение тока i равно I(р). Запишем изображение напряжения на L →u_L = L(di/dt) . По формуле (162), (di/dt) .=˙ р I(р) - i(0), где i(0) - значение тока i при t = 0. Следовательно,

U_L(p) = L(di/dt) .=˙ Lp I(p) - L i(0). ( 168 )

где i(0) = i(0_-) = i(0₊) - ток в индуктивном элементе в момент ком­мутации t =0, учитывающий начальные условия

 

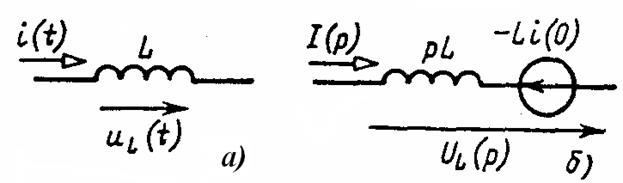
Рис.30. Схема замещения индуктивности в операторную форму.

Если i(0) = 0, то

L(di/dt) .=˙ Lp I(p) (169)

5.11. Изображение напряжения на конденсаторе.

Напряжение на конденсаторе ис часто записывают в виде и_с = -(1|C)∫ i_cdt, где не указаны пределы интегрирования по времени. Более полной является следующая запись:

и_с = и_с(0) + (1|C)∫ i_cdt ( 170 )

где учтено, что к моменту времени t напряжение на конденсаторе опре­деляется не только током, протекшим через него в интервале времени от 0 до t, но и тем напряжением и_с(0), которое на нем было при t = 0.

В соответствии с формулой (166) изображение — (1|C)∫ i_cdt равно

I(p)/ (С р), а изображение постоянной и_с(0) есть постоянная, деленная на р. Поэтому изображение напряжения на конденсаторе записыва­ют следующим образом:

и_с = I(p)/ Ср + и_с(0) / р ( 171 )

Рис.31. Схема замещения конденсатора в операторной форме

Приведем простейшие операторные соотношения; часть их была вы­ведена ранее, другая дается без вывода:

Частный случай и_с(0_-) = 0 для емкостного элемента

и_с = I(p)/ Ср ( 172 )

На следующей странице приведены формулы соответствия отдельных функций.

Отметим некоторые свойства преобразования Лапласа, называемые также теоремами.