 |
|
Некоторые теоремы и предельные соотношения.
5.12.1 .Теорема смещения в области оригиналов (теорема запаздывания).
Если изображение функции f(t) равно F(p), то изображение функции f(t - τ) равно е – pτ F(p).
Теорема доказывается путем подстановки f(t - τ) в формулу преобразования Лапласа и введения новой переменной (t - τ) = t1 ; dt = dt1; е – pt = е – pτ е – pτ
о∫∞ е –рt f(t - τ) dτ = е –рt о∫∞ е –рt1 f(t1) dt1 = е – pτ F(p) ( 173 )
5.12.2.Теорема смещения в области изображений.
Если изображению функции F(p) соответствует функция f(t), то изображению F(p-λ) — функция е – λt∙ f(t).
Доказательство проводят путем подстановки функции е – λt ∙f(t) в формулу преобразования Лапласа:
о∫∞ е –рt f(t - τ) dτ = о∫∞ е – t(р-λ)f(t) dt = F(p - λ) ( 174 )
Пример . Найти оригинал 1/(р + λ)2, если известно, что 1/р2 = t.
Решение: 1/(р + λ)2 .=˙ е –λt t.
5.12.3.Теорема об изменении масштаба {теорема подобия).
Если функции f(t) соответствует изображение F(p), то функции f(λt)— изоб-
ражение — (1/α)F(р/α).
Теорема доказывается следующим образом:
о∫∞ е –рt е -λt f( α τ) dt = (1/α) о∫∞ е –(р/α ) αt f( α t) d(αt)= (1/α)F(р/α) ( 175 )
4. Нахождение начального значения функции времени f(0+) по изображению функции F(p):
f(0+) = lim pF(p)при р → ∞ ( 176 )
Это соотношение получим, если в (8.39) р устремим к бесконечности. При этом левая часть (8.39) равна нулю.
5.12.4. Нахождение установившегося значения функции времени f(∞) по
изображению функции F(p):
f(∞) = lim p F(p) , при р→ 0 ( 177 )
Соотношение получим, если в (161) р устремим к нулю и учтем, что е-рt р→о =1
В результате имеем
о∫∞ df(t) = f(∞) - f(0) = lim p F(p) - f(0+), при р→ 0 ( 178 )
или
f(0) |t→∞ = limp F(p) |p→0.
Если искомая функция f(t) в послекоммутаиионном режиме содержит в своем составе периодическую составляющую (принужденную или свободную), то понятие f(∞) для нее оказывается неопределенным. Например, не имеет определенного смысла функция sin ωt при t = ∞. В соответствии с этим к цепям с синусоидальными источниками не следует применять предельное соотношение п. 5. Точно так же не следует пользоваться им для цепей без синусоидальных источников, если эти цепи чисто реактивные и не содержат резисторов. Так, при подключении последовательно соединенных L и С (при нулевых начальных условиях) к единичному напряжению 1(t) по цепи протекает свободная составляющая тока, численно равная √ C/L sin(L/√LC. В этом случае определять f(∞) как lim p F(p) также не имеет смысла.
5.12.6. Дифференцирование в области изображений.
Если F(p) .=˙ f(t), то - [dF(p)/dp] .=˙ t ∙f(t) Доказательство:
- d{ о∫∞ е –рt f(t) dt} /dp = - о∫∞ f(t) { d е –рt /dp} dt =- о∫∞ f(t) е –рt dt ( 179 )
Например, если f(t) = е –αt; F(p) = 1/(р + α) ; то
t е –αt –[dF(p)/dp ] = 1/ (р + α)2 ( 180 )
5.12.7. Интегрирование в области изображений.
Если при t ≥ 0 f(t) и f(t) /t преобразуемы по Лапласу и р∫∞ F(p)dp существует, то
р∫∞ F(p)dp .=˙ f(t) /t ( 181 )
Доказательство:
р∫∞ F(p)dp = 0∫∞ { 0∫∞ f(t) е –рt dt}dp = 0∫∞ f(t) { 0∫∞ е –рt dp}dt =
= 0∫∞ f(t){ е –рt /t}|p∞dt = 0∫∞{ f(t) /t} е –рt dt ( 182 )
Например, если f(t) = 1-е -αt (α > 0), F(p) = α \ р(р+α) ,
(1-е –αt) /t .=˙ р∫∞ {α/ р(р+α)}dp = р∫∞ {(1/ р) – 1/(р+α)}dp = ln {(р+α) /р}
5.13. Закон Ома в операторной форме.
Внутренние ЭДС. На рис.32 изображена часть сложной разветвленной электрической цепи. Между узлами а и b этой цепи включена ветвь, содержащая R, L, С и источник ЭДС e(t). Ток по ветви обозначим через i.

Рис.32. Участок электрической цепи
Замыкание ключа К в схеме приводит к переходному процессу. До коммутации ток i = i(0-) и напряжение на конденсаторе uc = и(0-). Выразим потенциал в точке а через потенциал точки b для послекоммутационного режима:
φа = φb + uc+ uL + uR - e(t) ( 183 )
uаb = φа - φb = uc+ uL + uR - e(t)
Вместо uL запишем L(di/dt), вместо ис соответственно
uc = ucо+(1/С) ∫ idt .
Тогда
uаb = i R + L(di/dt) + ис(0) + 1/С) ∫ idt - e(t). (184)
К уравнению (184) применим преобразование Лапласа. Преобразование Лапласа является линейным, поэтому изображение суммы равно сумме изображений.
Каждое слагаемое уравнения (184) заменим операторным изображением: вместо iR запишем R I(р); вместо
uаb - Uаb(р) L(di/dt) .=˙ L p I(p) – L i(0)
ис(0) .=˙ ис(0)/р 1/С) ∫ idt .=˙ I(p)/Ср
Слагаемое L i(0) представляет собой внутреннюю ЭДС, обусловленную запасом энергии в магнитном поле индуктивной катушки вследствие протекания через нее тока i(0) непосредственно до коммутации. Слагаемое ис(0)/р представляет собой внутреннюю ЭДС, обусловленную запасом энергии в электрическом поле конденсатора вследствие напряжения на нем ис(0) непосредственно до коммутации.
В соответствии с формулой (184) на рис.33 изображена операторная схема замещения участка цепи рис.32.Операторные сопротивления ее R, pL,
[1/(С р)]. Как следует из формулы (185), внутренняя ЭДС L i(0) направлена согласно с направлением тока I(p), внутренняя ЭДС Uc(0)/ р —встречно току I(p). В результате найдем
 Uab(p) = {I(p)[R + pL + (1/Cp)] + Li(0) - ис(0)/р + E(p)}/Z(p) (185)
Uab(p) = {I(p)[R + pL + (1/Cp)] + Li(0) - ис(0)/р + E(p)}/Z(p) (185)
Рис.33. Операторная схема замещения.
Смысл проведенного преобразования состоит в том, что вместо дифференциального уравнения (184) получили алгебраическое уравнение (185), связывающее изображение токаI(p) с изображением ЭДС Е(р) и изображением напряжения Uab(p). Из уравнения (185) следует, что
I(p) = {Uab(p)+ Li(0) - ис(0)/р + E(p)} /Z(p) ( 186 )
где Z(p) = R + р L +[1/(С р)]. операторное сопротивление участка цепи
между точками а и Ь. Структура его аналогична структуре комплекса сопротивления того же участка цепи переменному току, если jω заменить на р .
Как указывалось ранее, комплексное число р = а + j b может быть записано в виде р = j (b- j a) = jΩ, где Ω = b - j a — комплексная частота;
Z(p) = Z(j Ω) — сопротивление, оказываемое рассматриваемой цепью воздействию Ůе-jΩt = Ůе-jpt , подобно тому как Z(jω ) есть сопротивление, оказываемое воздействию Ůе-jωt . Поэтому Z(p) называют сопротивлением на комплексной частоте.
Уравнение (186) может быть названо законом Ома в операторной форме для участка цепи, содержащего ЭДС. Оно записано при ненулевых начальных условиях.
В частном случае, когда на участке ab отсутствует ЭДС е(t) и к моменту коммутации i(0) = 0 и ис(0) = 0, уравнение (186) приобретает более простой вид:
I(p) = Uab(p)/ Z(p) ( 187 )
Уравнение (187) есть математическая запись закона Ома в операторной форме для участка цепи, не содержащего источник ЭДС при нулевых начальных условиях.
5.14. Первый закон Кирхгофа в операторной форме.
По первому закону Кирхгофа, алгебраическая сумма мгновенных значений токов, сходящихся в любом узле схемы, равна нулю. Так, для узла а схемы на рис. 32
i1 +i2+ i3 =0. (188)
Воспользовавшись линейностью преобразования Лапласа для суммы токов в любом узле цепи к=1∑n iк (t) = 0 воспользуемся тем, что изображение~суммы равно сумме изображений:
I(p)1 + I(p)2 + I(p)3 = 0 ( 189 )
В общем случае
∑I/(р) = 0 ( 190)
где Iк(p) .=˙ L[ik(t)]
Уравнение (190) выражает собой первый закон Кирхгофа в операторной форме.
5.14. Второй закон Кирхгофа в операторной форме.
Для любого замкнутого контура любой электрической цепи можно составить уравнение по второму закону Кирхгофа для мгновенных значений. Предварительно необходимо выбрать положительные направления для токов в ветвях и направление обхода контура.
к=1∑n ик (t) = 0 ( 191 )
или в другой форме
к=1∑n ик (t) = к=1∑n ек (t)
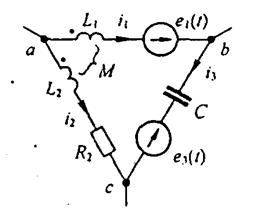
Рис.34. Участок цепи в виде контура
Запишем уравнение по второму закону Кирхгофа для контура на рис.34. Контур обходим по часовой стрелке. Учтем, что индуктивности L1 и L2 связаны магнитно. При выбранных положительных направлениях для токов i1, и i2 между L1 и L2 имеет место согласное включение.
Падение напряжения на L1 равно L1(di1 /dt) + М(di2 /dt); на L2 - L(di1 /dt) + М(di2 /dt);
При составлении уравнения учтем, что начальное напряжение на конденсаторе равно ис(0-) . Пусть оно действует согласно с током i3. Начальное значение i1 = i1 (0); тока i2 = i2 (0).
В результате имеем
L(di1 /dt) + М(di2 /dt) + ис(0-) + 1/С) ∫ idt - i2R2 - L(di1 /dt) - М(di2 /dt) = е1(t)- е3(t)
( 192 )
Каждое из слагаемых (192) заменим операторным изображением:
L1(di1 /dt) .=˙ L1 p I1(p) – L1 i1 (0) ; М(di2 /dt) .=˙ М p I2 (p) – М i2 (0);
1/С) ∫ i3 dt .=˙ I3(p) / Ср; i2R2 .=˙ I2(p) R2 ;
L2(di2 /dt) .=˙ L2 p I2(p) – L2 i2 (0) ; М(di1 /dt) .=˙ М p I1 (p) – М i1 (0);
е1(t) = Е1(р); е2(t) = Е2(р) ( 193 )
Подставив (193) в (192), объединим слагаемые с I1(p) , I2(p) , I3(p) перенесем в правую часть ис(0)/р, L1 i1 (0) и другие внутренние ЭДС. В результате получим
I1(p)Z1(p) + I2(p)Z2(p) + I3(p)Z3(p) = Е1(р) - Е3(р) + Евн(р) ( 194 )
где
Z1(p) = p(L1 -М); Z2(p)=p(M - L2); Z3(p)=l/(Cp);
Е(р) = (L1 -М)i1(0) + ( M - L2) i2(0) - ис(0)/р
В более общем виде уравнение (194) можно записать так:
к=1∑m Uк(р) = 0 ( 195 )
или
∑ Iк(p)Zк(p) = ∑ Ек(р) ( 196 )
где Uk (р) .=˙ f[uk (t)] и Ек(р) .=˙ f[ek(t) ].
Уравнение (196) представляет собой математическую запись второго закона Кирхгофа в операторной форме. В состав Ек(р) в общем случае входят и внутренние ЭДС.
5.16. Составление уравнений для изображений путем использования методов, рассмотренных в третьей главе.
Из уравнений, составленных по законам Кирхгофа для мгновенных значений, вытекают соответствующие уравнения для изображений.
Уравнения для изображений по форме аналогичны уравнениям, составленным для той же цепи с помощью символического метода для комплексов токов и напряжений.
Но если каждому уравнению для комплексов отвечает соответствующее уравнение для изображений, то все основанные на законах Кирхгофа приемы и методы составления уравнений (методы эквивалентного генератора, контурных токов, узловых потенциалов, наложения и т. п.) можно применить и при составлении уравнений для изображений.
При составлении уравнений для изображений ненулевые начальные условия учитывают путем введения «внутренних» ЭДС, обусловленных начальными токами через индуктивные элементы и начальными напряжениями на конденсаторах.