 |
|
Глава 7. Интеграл Дюамеля.
Познакомимся с третьим методом расчета переходных процессов в линейных электрических цепях — расчетом с помощью интеграла Дюамеля.
При использовании интеграла Дюамеля переменную, по которой производится интегрирование, обозначим τ а под t по-прежнему будем понимать тот момент времени, в который требуется найти ток в цепи. Пусть к цепи с нулевыми начальными условиями в момент времени t = 0 подключается напряжение и(τ) (рис. 35).
Для того чтобы найти ток в цепи в момент времени t, заменим плавную
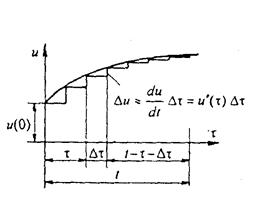 кривую ступенчатой и просуммируем напряжения от начального напряжения и(0) и от всех ступенек напряжения, вступающих в действие с запозданием во времени.
кривую ступенчатой и просуммируем напряжения от начального напряжения и(0) и от всех ступенек напряжения, вступающих в действие с запозданием во времени.
Напряжение и(0) в момент времени t вызовет в цепи ток и(0) g(0), где g(0)— переходная проводимость. В момент
Рис.35
времени τ + Δτ (см. рис.35) возникает скачок напряжения
Δ u ≈(du/dτ)Δτ = и′(τ) Δτ ( 218 )
Для того чтобы найти составляющую тока в момент времени t, вызываемую этим скачком, напряжения Δ u , необходимо и′(τ) Δτ умножить на значение переходной проводимости с учетом времени действия скачка до момента времени t. Из рис.35 видно, что это время равно t -.τ – Δτ. Следовательно, приращение напряжения от этого скачка составляет и′(τ)g(t -.τ – Δτ) Δτ.
Полный ток в момент времени t получим, если просуммируем все частичные токи от отдельных скачков и прибавим их к току и(0) g(0): i(t) = и(0) g(t) +∑ и′(τ)g(t - τ – Δτ) Δτ
Число членов суммы равно числу ступенек напряжения. Очевидно, что ступенчатая кривая тем лучше заменяет плавную кривую, чем больше число ступенек. С этой целью заменим конечный интервал времени Δτ на бесконечно малый dτ и перейдем от суммы к интегралу:
i(t) = u(0) g(t) + o∫t и′(τ)g(t - τ – Δτ) Δτ ( 219 )
Формулу (219) называют интегралом Дюамеля.
С помощью интеграла Дюамеля можно найти не только ток, но и любую другую физическую величину, например напряжение. В этом cлучае в формулу вместо переходной проводимости g(t) будет входить переходная функция h(t), если на входе цепи действует источник ЭДС (напряжения), и переходное сопротивление R(t), если на входе цепи действует источник тока.
7.1. Последовательность расчета с помощью интеграла Дюамеля. Расчет с помощью интеграла Дюамеля проводят в четыре этапа:
1)определение переходной проводимости g(t) (переходной функции h(t)) для исследуемой цепи;
2)нахождение g(t-τ) [h(t-τ)]. С этой целью в формуле для g(t) [h(t)] заменяют t на (t - τ);
3)определение u'(т). Для этого находят производную от заданного напряжения u(t) по времени t и в полученном выражении заменяют t на τ;
4)подстановка найденных на этапах 1-3 функций в формулу (8.75), интегрирование по переменной τ и подстановка пределов.
Пример 101. Найти i1, =f(t) и и2 =f(t) при замыкании ключа на схеме рис. 8 40. Напряжение источника ЭДС u(t) = 100(1-е-αt) В; α = 0,25с-1, R= 0,5Ом; L1 = 1 Гн; М = 0.5 Гн.
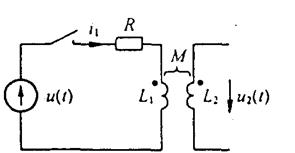
Рис.36. Расчетная схема замещения
Решение. Переходная проводимость цепи, состоящей из последовательно включенных R и L.
g(t) = (1/R)(1-е-bt)
где
b = R/L
g(t - τ) = (1/R)(1-е-b(t – τ))
Первое слагаемое в формуле (219) выпадает, так как и(0) = 0. При этом
и'(t) = d[ 100(1- е-αt)] /dt =100 α е-αt
и'(τ) = 100 α е-ατ
i1 (t)= о∫t и'(τ) g(t - τ) dt = [100α/R] о∫t е-αt (1-е-b(t – τ))dτ
При интегрировании учитываем, что е-bt от .х не зависит
i1 (t)= 200(1+ е-0,5t - 2е-0,25t ), А.
Напряжение на зажимах вторичной обмотки
u2(t) = M(di1 /dt) = 50( е-0,25t - е-0,5t ), В
7.2. Применение интеграла Дюамеля при сложной форме напряжения.
Пусть напряжение u(t) изменяется во времени по сложному закону, например в соответствии с рис.37. Начальное напряжение равно и(0). В интервале от t = 0 до t = t1 напряжение плавно растет и закон его изменения u1(t). В момент t = t1 оно меняется скачком от иа до ub, а затем снова изменяется, но уже по другому закону и2(t) во времени. При t = t2 напряжение скачком уменьшается от ис до нуля.
Требуется найти ток в каждом из трех интервалов времени. Под первым интервалом будем понимать интервал времени от t = 0 до t = t1 (не включая скачка напряжения от иа до иb); под вторым — от t1 до t2, включая скачок от
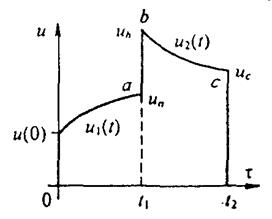 иа до иb, но не включая скачок от ис до 0; под третьим — при t > t2, включая скачок от ис до 0.
иа до иb, но не включая скачок от ис до 0; под третьим — при t > t2, включая скачок от ис до 0.
Интегрирование по-прежнему проводим по τ, понимая под t фиксированный момент времени, в который требуется найти ток. На основании принципа нало
Рис.37
жения ток в любой момент времени t определится как сумма токов от всех напряжений, воздействовавших на цепь до момента t.
В первый интервал времени
i (t)= u(0) g(t) + o∫t и'(τ) g(t - τ) dτ ( 220 )
Во второй интервал времени
i (t)= u(0) g(t) + o∫t и'(τ) g(t - τ) dτ + (ua - ub) g(t – t1) + t1∫t2 и2'(τ) g(t - τ) dτ (221 )
где слагаемое (ua - ub)g(t – t1) обусловлено скачком напряжения от ua и ub в момент времени t1.
В третий интервал времени
i (t)= u(0) g(t) + o∫t и'(τ) g(t - τ) dτ + (ua - ub) g(t – t1) + t1∫t2 и2'(τ) g(t - τ) dτ +
+ (0-uc) g(t – t2) ( 221 )
Пример 102. В электрической цепи (см. рис. 8.40) в момент времени t = 0 замыкается ключ и напряжение и(t) изменяется в соответствии с рис.37; u(0) = 50 В. В первый интервал времени от t = 0 до t = t1 = 4,с напряжение
u1(t) = 150 – 100е -αt1, где α = 0,25 с-1. Во второй интервал времени от ; t = t1 = 4,с до t = t2 =6,с и2(t) = 50 + 100e-c(t-t1) , где c = 0.4с-1. Параметры схемы (см. рис. 8.40) R = 0,5Ом; L1 = 1 Гн (вторичная цепь разомкнута).
Найти закон изменения тока i1 во времени для обоих интервалов времени, а также знаения тока i1 при t, равном 2 и 5 с
Решение. В соответствии с § 8.54 переходная проводимость
g(t) = (1/R) (1-е-bt ); b =(R/L) = 0,5c-1; g(t - τ) =(1/R) (1-е-b(t – τ) );
В первый интервал времени и'(t) = 100 α е –ατ . Поэтому
i1 (t)= u(0) g(t) + o∫t и'(τ) g(t - τ) dτ = [u(0)/R](1 – e-bt) +(100α/R) o∫t е –ατ(1-е-b(t – τ))dτ =
= 100(1- е-0,5t) + 200(1 + е -0,5t – е -0,25t )
При t=2с i1 (t)= 100(1- е -1) + 200(1 + е -1 – 2е -0,5 ) = 94,9 А
Во второй интервал времени (включая скачок ( ub- ua ) = 36,9 В
i1 (t)= u(0) g(t) + o∫t и'(τ) g(t - τ) dτ + (ua - ub) g(t – t1) + t1∫t2 и2'(τ) g(t - τ) dτ
и2'(τ) =100c е –сτесt1 ;
i1 (t)= 100(1- е-0,5t) + 200(0,632 – 1,718 е -0,5t) + (39,6/0,5) (1-е-0,5(t-t1) ) –
- [100c/R(b-c)]{ -(b/c)e-ct + [(b-c)/c ]e –ct1 + e –ct1 e-c(t – t1) } e –ct1
При t = 5 с i1 = 204,32 А
7.3. Сравнение различных методов расчета переходных процессов. Классический и операторный методы расчета теоретически можно применять для решения задач любой сложности. Каким из них пользоваться, во многом зависит от навыка и привычки.
Однако классический метод физически более прозрачен, чем операторный, в котором решение уравнений во многом формализовано.
Если при сравнении методов исходить из объема вычислительной работы, то решение уравнений первого, второго, а иногда и третьего порядков для источников постоянной (синусоидальной) ЭДС или тока целесообразно проводить классическим методом, а решение уравнений более высоких порядков — операторным. Объясняется это тем, что чем выше порядок характеристического уравнения, тем более громоздкой и трудоемкой оказывается операция нахождения постоянных интегрирования в классическом методе. Операторный метод имеет перед классическим явное преимущество при решении задач, в которых определение принужденной компоненты искомой величины оказывается затруднительным вследствие сложного характера вынуждающей силы, а также при решении уравнений в частных производных . Если воздействующее напряжение изменяется во времени, например линейно или в виде всплеска одной или нескольких экспонент, рекомендуется применять операторный метод или интеграл Дюамеля. Но основной областью применения интеграла Дюамеля являются случаи, когда напряжение изменяется по сложному закону во времени, например при наличии скачков напряжения , или когда переходная проводимость g(t) и (или) воздействующее на схему напряжение заданы графически (в последнем случае интеграл Дюамеля берется путем численного интегрирования).
Рассматриваемый метод расчета переходных процессов, получивший название метода пространства состояний, используется главным образом, когда расчет осуществляется с применением ЭВМ. Для ручного счета этот метод громоздок.
Классический и операторный методы, а также метод пространства состояний в аналитической форме и интеграл Дюамеля имеют общий недостаток: необходимость определения всех корней характеристического уравнения, что для уравнений высоких степеней (например, 5-, 6-, 7-й, ...) требует много времени. В этих случаях может быть рекомендовано числовое решение на ЭВМ уравнений, составленных по методу пространства состояний; может быть применен и спектральный метод в том виде, в каком он рассмотрен, например, в гл. 9. Кроме того, в этих случаях используют моделирующие установки.