 |
|
Означення 8. Добутком многочленів
Розділ I. Многочлени від однієї змінної
Кільце многочленів. Алгебраїчна і функціональна рівність многочленів. Відношення подільності в кільці многочленів. Ділення з остачею.
Означення 1. Многочленом (поліномом) від однієї змінної над областю цілісності Rназивається вираз виду:
 , де
, де
 - довільне ціле невід’ємне число,
- довільне ціле невід’ємне число,
 – елементи R,
– елементи R,
 – деякі символи;
– деякі символи;
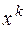 - k-ий степінь змінної
- k-ий степінь змінної  ,
,
 - k-ий коефіцієнт многочлена або коефіцієнт при
- k-ий коефіцієнт многочлена або коефіцієнт при  (k=
(k=  ).
).
Приклад: 

Означення 2. Область цілісності – це комутативне кільце з 1 без дільників нуля ( R[x] - сукупність всіх многочленів над областю цілісності ).
Означення 3.Вираз  (k =
(k =  ) називається k-тим
) називається k-тим
членом або членом k-го степеня многочлена  ,
,  - нульовимабо вільним членом.
- нульовимабо вільним членом.
Якщо 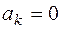 (тобто є нульовим елементом області цілісності R), то кажуть, що k-тий член многочлена
(тобто є нульовим елементом області цілісності R), то кажуть, що k-тий член многочлена  дорівнює нулю або його немає.
дорівнює нулю або його немає.
Означення 4.Відмінний від нуля член многочлена  , степінь якого більший за степінь усіх інших, відмінних від нуля членів цього многочлена, називається старшим членом, його коефіцієнт – старшим коефіцієнтом, а його степінь – степенем многочлена.
, степінь якого більший за степінь усіх інших, відмінних від нуля членів цього многочлена, називається старшим членом, його коефіцієнт – старшим коефіцієнтом, а його степінь – степенем многочлена.
З попереднього прикладу:
5  – старший член, 5 – старший коефіцієнт,
– старший член, 5 – старший коефіцієнт,
4 – степінь многочлена.
Степінь  позначають deg f.
позначають deg f.
Означення 5.Елемент 0  R вважаємо константою і многочленом над R. Його називають нуль-многочленом, і позначають
R вважаємо константою і многочленом над R. Його називають нуль-многочленом, і позначають  , тобто
, тобто 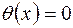 .
.
Означення 6. Канонічною формою многочлена  називається такий запис, коли члени многочлена упорядковано за спаданням степеня
називається такий запис, коли члени многочлена упорядковано за спаданням степеня 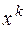 .
.
Приклад:  - канонічна форма, а
- канонічна форма, а
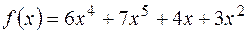 - не канонічна форма запису многочлена.
- не канонічна форма запису многочлена.
Означення 7. Сумою многочленів
 називають многочлен
називають многочлен
 ,
,
Наслідок 1. Степінь суми двох многочленів не перевищує більшого з степенів даних многочленів:
deg (  +
+  ) ≤ max (deg
) ≤ max (deg  , deg
, deg  ).
).
Наслідок 2. Для довільного многочлена 

Означення 8. Добутком многочленів
 називається многочлен
називається многочлен  , де
, де  ,
,  , тобто
, тобто  .
.
Наслідок 3. Якщо  і
і  не є нуль-многочленом, то
не є нуль-многочленом, то
deg ( 
 ) = deg
) = deg  + deg
+ deg  .
.
Наслідок 4. Якщо  =
=  , то
, то 
 =
=  .
.
Означення 9. Якщо многочлен 
 R[x], має канонічну форму, i
R[x], має канонічну форму, i 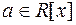 , то елемент
, то елемент 
 з
з
кільця R називається значенням многочлена 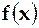 при
при  і
і
позначається  .
.
Якщо 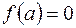 , то число
, то число  називається коренем
називається коренем
многочлена  .
.
Означення 10. Многочлени  і
і  називаються рівнимиміж собою
називаються рівнимиміж собою  =
=  , якщо їх канонічні форми збігаються: мають однакові степені і попарно рівні відповідні коефіцієнти (алгебраїчна рівність многочленів).
, якщо їх канонічні форми збігаються: мають однакові степені і попарно рівні відповідні коефіцієнти (алгебраїчна рівність многочленів).
Означення 11. Кожен многочлен 
 R[x] визначає відображення
R[x] визначає відображення  jf = R®R таке, що jf (
jf = R®R таке, що jf (  ) =
) =  .
.
Якщо область цілісності R має характеристику 0, то многочлени  і
і 
 R[x] рівні тоді і тільки тоді, коли рівні функції jf і jg, які вони визначають (функціональна рівність многочленів).
R[x] рівні тоді і тільки тоді, коли рівні функції jf і jg, які вони визначають (функціональна рівність многочленів).
Алгебраїчне і функціональне тлумачення многочленів рівносильні над областю цілісності характеристики 0.
Якщо многочлени рівні алгебраїчно, то очевидно вони рівні і функціонально. Обернене твердження не виконується.
Означення 12.Нехай Р- деяке поле. Многочлен 
 P[x] ділиться націло на
P[x] ділиться націло на 
 P[x] ( записується
P[x] ( записується 

 ), якщо існує многочлен
), якщо існує многочлен 
 P [x] такий, що
P [x] такий, що  =
= 
 .
.
Відношення подільності многочленів над полем Р має такі властивості:
1)  [
[ 





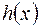 Þ
Þ 

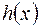 ;
;
2) 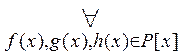 [
[ 

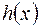



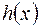 Þ
Þ
Þ (  ±
±  )
) 
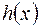 ];
];
3)  [
[ 

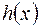 Þ
Þ 

 P
P 


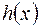 ];
];
4) 
 [
[ 
 c];
c];
5)  [
[ 





 Þ
Þ
Þ 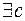
 P [x]
P [x]  = c
= c  ];
];
6) 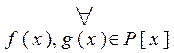
 [
[ 

 Þ
Þ
Þ 
 c
c  ];
]; 
7) 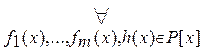 [
[ 

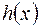



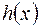
 …
… 

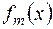

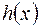 Þ
Þ
Þ  [(
[( 
 + … +
+ … + 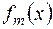
 )
) 
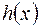 ].
].
Означення 13. У кільці Р[x] многочлени  і
і  асоційовані, якщо вони відрізняються лише множником, який є відмінною від нуля константою:
асоційовані, якщо вони відрізняються лише множником, який є відмінною від нуля константою:
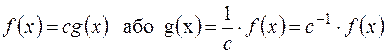 .
.
Теорема 1. Довільний многочлен 
 Р[x] ділиться з остачею на будь-який многочлен
Р[x] ділиться з остачею на будь-який многочлен 
 Р[x],
Р[x],  ¹ 0; при цьому частка
¹ 0; при цьому частка  і остача
і остача  належать Р[x] і визначаються однозначно, тобто
належать Р[x] і визначаються однозначно, тобто
 , причому
, причому  або deg
або deg  < deg
< deg  , де
, де
 -ділене,
-ділене,  - дільник,
- дільник,  - частка,
- частка,  - остача.
- остача.
Для знаходження частки і остачі від ділення многочлена  на
на  над полем Р використовують різні методи: ділення “кутом”, метод невизначених коефіцієнтів, табличні схеми.
над полем Р використовують різні методи: ділення “кутом”, метод невизначених коефіцієнтів, табличні схеми.