|
|
ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ.
 1.1.Знайти всі цілі числа
1.1.Знайти всі цілі числа  і
і  , при яких многочлен
, при яких многочлен  є квадратом деякого многочлена
є квадратом деякого многочлена  з кільця
з кільця  , та записати многочлен
, та записати многочлен  .
.
Розв’язання.
Многочлен 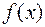 має степінь 4. Тому степінь шуканого многочленна
має степінь 4. Тому степінь шуканого многочленна
 (якщо він існує!) рівна 2. Нехай
(якщо він існує!) рівна 2. Нехай  і
і  . Запишемо многочлен
. Запишемо многочлен  у канонічній формі:
у канонічній формі:
 .
.
Так як ці многочлени рівні, то маємо систему рівнянь:

З першого і останнього рівнянь системи знаходимо, що  .Це означає, що система рівна сукупності чотирьох систем:
.Це означає, що система рівна сукупності чотирьох систем:



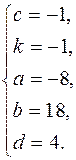
Отже, при 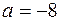 і
і 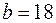 многочлени
многочлени  і
і  мають вигляд:
мають вигляд:
 При
При 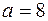 і
і  отримуємо такі многочлени:
отримуємо такі многочлени: 
1.2.Довести, що з функціональної точки зору наступні многочлени дорівнюють один одному:  з кільця
з кільця  .
.
Розв’язання.
 - остачі від ділення на 3 (лишки за модулем 3).
- остачі від ділення на 3 (лишки за модулем 3).
З функціональної точки зору многочлени рівні, якщо рівні між собою функції jf і jg , які вони визначають, тобто, якщо функції набувають однакових значень при однакових лишках:
 
| 
| 
| 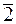
|
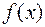
| 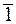
| 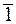
| 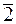
|

| 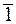
| 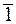
| 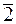
|

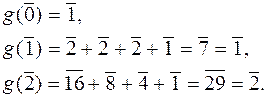
Отже, 
1.3.Знайти суму коефіцієнтів многочлена:  у кільці
у кільці  .
.
Розв’язання.
Сума коефіцієнтів дорівнює значенню многочлена при  .
.

1.4. Знайти остачу від ділення  на
на  у кільці Z[x].
у кільці Z[x].
Розв’язання.
Для многочленів  i
i  в кільці Z[x] застосуємо теорему про ділення з остачею. Тоді існують такі многочлени
в кільці Z[x] застосуємо теорему про ділення з остачею. Тоді існують такі многочлени  i
i  , що
, що
 =
= 
 +
+  i deg
i deg  < 2. Тоді
< 2. Тоді 
Тому можемо записати таку рівність:
 .
.
Враховуючи, що g (-1) = g (1) = 0, то підставивши ці значення замість  у рівність матимемо:
у рівність матимемо:
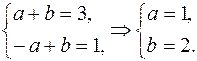
Тому  =
=  + 2.
+ 2.
1.5.Остачі від ділення многочленів  на
на 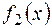 в кільці Q[x] відповідно дорівнюють
в кільці Q[x] відповідно дорівнюють  ,
, 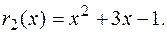 Знайти остачу від ділення многочлена
Знайти остачу від ділення многочлена  на g (x).
на g (x).
Розв’язання.
За теоремою про ділення з остачею маємо:

Запишемо умову задачі згідно цих розкладів: 
Звідси маємо, що шукана остача 
 .
.
Ділення многочлена на двочлен ( x-a ). Теорема Безу. Схема Горнера. Розклад многочлена за степенями ( x-a). Найбільший спільний дільник і найменше спільне кратне многочленів. Алгоритм Евкліда.
Теорема Безу. Для будь-якого елемента a з поля Р остача при діленні многочлена 
 P[x] на (
P[x] на (  – a) дорівнює
– a) дорівнює  (a).
(a).
Наслідок. Якщо  = a є коренем
= a є коренем  , то
, то 
 (
(  - a).
- a).
Приклад.1 Поділити многочлен на двочлен(  – a ) можна “кутом”:
– a ) можна “кутом”:

_4x4 + x3 - ділене |x + 1 + i - дільник
4x4 + (4 + 4i) x3 |4x3 – (3 + 4i) x2 + (7i - 1) x + 8 – 6i =  - частка
- частка
_-(3 + 4i) x3
-(3 + 4i) x3 – ( 1+ i)(3 + 4i) x2
_(7i - 1) x2 
(7i - 1) x2 + (1 + i)(7i - 1) x
_(8 - 6i) x
(8 - 6i) x + (1 + i)(8 - 6i)
-2i - 14 =  - остача
- остача
2. Метод невизначених коефіцієнтів :
4  4 +
4 +  3 = (
3 = (  + 1 + i)
+ 1 + i)  +
+  , deg
, deg 
 3, deg
3, deg  < 2
< 2
тому  = A3
= A3  3 + A2
3 + A2  2 + A1
2 + A1  + A0,
+ A0,
 = B1
= B1  + B0
+ B0
4  4 +
4 +  3 = (
3 = (  + 1 + i)( A3
+ 1 + i)( A3  3 + A2
3 + A2  2 + A1
2 + A1  + A0) + B0
+ A0) + B0
маємо:
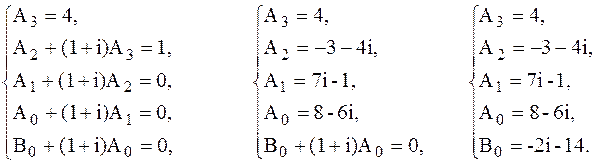
тому  = 4
= 4  3 – (3 + 4i)
3 – (3 + 4i)  2 + (7i - 1)
2 + (7i - 1)  + 8 – 6i
+ 8 – 6i
 = -2i - 14.
= -2i - 14.
3. Схема Горнера:
a = -1 - i
| Робоча стрічка |   4 4
|   1 1
|   0 0
|   0 0
|  0 0
| |||||||||||||||
-1 - i
| 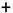 4 4
A3 | -3 - 4i
| 7i – 1
A1 | -6i + 8
A0 | 2i - 14 =  B0
B0
|
При кожному наступному діленні старший коефіцієнт переписується, а робочою стрічкою стає щойно написана стрічка з коефіцієнтів.
Розкласти многочлен за степенями ( x - a ) означає представити його у вигляді:  = cn (
= cn (  - a )n + cn-1 (
- a )n + cn-1 (  - a )n-1 + … + c1 (
- a )n-1 + … + c1 (  - a ) + c0
- a ) + c0
Це зручно робити за схемою Горнера, де с0, с1,..., сn являються частками при послідовному діленні многочлена  на (
на (  - a).
- a).
Приклад: Розкласти многочлен  =
= 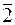
 4 +
4 +  3 +
3 +  2 +
2 + 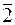 за степенями
за степенями
(  - a),
- a),  =
=  в кільці Z3[
в кільці Z3[  ].
].
Розв’язання.
Виконаємо послідовне ділення многочлена  на двочлен (
на двочлен (  -
-  ), використовуючи схему Горнера.
), використовуючи схему Горнера.

| 
| 
| 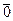
| 
| |

| 
|  = = 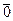
| 
| 
| 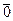 =С0 =С0
|

| 
| 
| 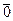
|  =С1 =С1
| |

| 
|  = = 
|  = С2 = С2
| ||

| 
| 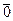 = С3 = С3
| |||

|  = С4 = С4
|
Маємо  =
= 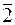 (
(  -
- 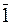 )4 + (
)4 + (  -
- 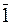 )2 + (
)2 + (  -
- 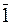 ).
).
Означення 1. Якщо многочлен 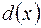 є дільником многочлена
є дільником многочлена  і многочлена
і многочлена  , то він називається спільним
, то він називається спільним
дільником f(x) i g(x).
Означення 2. Спільний дільник многочленів  і
і  , який ділиться на кожен інший спільний дільник
, який ділиться на кожен інший спільний дільник  і
і  , називається найбільшим спільним дільником (НСД) і позначається (f(x),g(x)).
, називається найбільшим спільним дільником (НСД) і позначається (f(x),g(x)).
Означення 3. Многочлени  і
і 
 Р[x] називаються взаємно простими, якщо їх спільний дільник є многочленом нульового степеня:
Р[x] називаються взаємно простими, якщо їх спільний дільник є многочленом нульового степеня:  .
.
Теорема 2. Для будь-яких двох многочленів  i
i 
 Р [x] існує НСД
Р [x] існує НСД 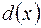 , такий, що
, такий, що 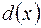 =
= 
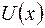 +
+ 
 .
.
Таке представлення називається лінійним представленням НСД, де 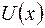 і
і  – деякі многочлени з Р[
– деякі многочлени з Р[  ].
].
Наслідок. Многочлени  i
i 
 Р[x] взаємно прості тоді і тільки тоді, коли існують такі многочлени
Р[x] взаємно прості тоді і тільки тоді, коли існують такі многочлени 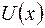 і
і 
 Р[x], що
Р[x], що

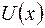 +
+ 
 = 1.
= 1.
Властивості взаємно простих многочленів:
1)  [(
[(  ,
,  ) = 1
) = 1  (
(  ,
, 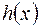 ) = 1
) = 1 
 (
(  ,
, 
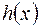 ) = 1
) = 1
2)  [
[ 



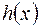
 (
(  ,
, 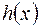 ) = 1
) = 1 



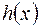 ]
]
3)  [
[ 





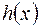
 (
(  ,
, 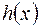 ) = 1
) = 1 




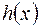 ]
]
Алгоритм Евкліда.
Маємо  і
і  , причому deg
, причому deg 
 deg
deg  . Виконаємо послідовне ділення :
. Виконаємо послідовне ділення :
 =
= 
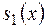 +
+ 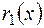
 =
= 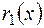
 +
+ 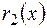
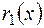 =
= 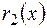
 +
+ 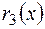
…
 =
= 
 +
+ 
 =
= 

Остання відмінна від нуля остача у цій системі рівностей  і є НСД многочленів
і є НСД многочленів  і
і  .
.
Властивості НСД:
1) будь-які многочлени  і
і  мають тривіальні НСД – дільники одиниці кільця Р[x];
мають тривіальні НСД – дільники одиниці кільця Р[x];
2) якщо 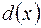 – НСД многочленів
– НСД многочленів  і
і  , то " с
, то " с  0 і
0 і  – теж НСД многочленів
– теж НСД многочленів  і
і  .
.
3) якщо 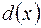 i
i 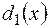 - НСД многочленів
- НСД многочленів  і
і  , то
, то 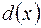

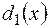 , бо
, бо
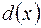 - НСД , а
- НСД , а 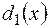

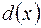 , бо
, бо 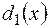 – НСД. Тоді
– НСД. Тоді 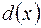 i
i 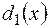 – aсоційовані, тобто
– aсоційовані, тобто 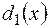 =
=  , де c – const, c
, де c – const, c  0.
0.
Зауваження:НСД можна обчислювати з точністю до сталого множника.
Приклад: Знайти НСД  =
=  4 +
4 +  3 +
3 +  2 +
2 +  + 1 i
+ 1 i
 = 5
= 5  3 + 4
3 + 4  2 + 3
2 + 3  + 2.
+ 2.
Розв’язання.
1) (  :
:  ) ( щоб уникнути дробів множимо
) ( щоб уникнути дробів множимо  на 5)
на 5)
x4 + x3 + x2 + x + 1 |5x3 + 4x2 + 3x + 2
_5x4 + 5x3 + 5x2 + 5x + 5 |x + 1 = 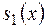 - частка
- частка
5x4 + 4x3 + 3x2 + 2x
x3 + 2x2 + 3x + 5
_5x3 + 10x2 + 15x + 25
5x3 + 4x2 + 3x + 2
6x2 + 12x + 23 = 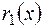 – остача
– остача
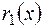 = 6x2 + 12x + 23.
= 6x2 + 12x + 23.
2) (  :
: 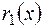 )
)
5x3 + 4x2 + 3x + 2 |6x2 + 12x + 23
_30x3 + 24x2 + 18x + 12 | 5x - 6 =  - частка
- частка
30x3 + 60x2 + 115x
_-36x2 -97x + 12
36x2 -72x - 138
-25x + 150 = 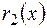 – остача
– остача
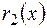 = -x + 6
= -x + 6
3) ( 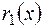 :
: 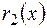 )
)
_6x2 + 12x + 23 |-x + 6
6х2 – 6х |-6x - 48 =  - частка
- частка
_48х + 23
48х - 288
311 / : 311
1= 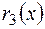 - остача
- остача
Отже 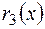 = 1, тому (
= 1, тому (  ) =1 – взаємно прості.
) =1 – взаємно прості.
Означення 4. Спільним кратним многочленів f(x) і
g(x)  Р[x] називають будь-який многочлен
Р[x] називають будь-який многочлен 
 Р[x] такий, що
Р[x] такий, що






 .
.
Найменшим спільним кратним (НСК) многочленів f(x) і g(x) називається їх спільне кратне, на яке ділиться кожне спільне кратне цих многочленів. Позначається так : [f(x),g(x)].
Теорема 3. Для будь-яких відмінних від нуля многочленів  і
і  НСК існує і визначається однозначно з точністю до сталого множника.
НСК існує і визначається однозначно з точністю до сталого множника.
[  ,
,  ] =
] =