 |
|
Відокремлення кратних множників.
Представляємо многочлен у вигляді добутку  ,
,
де  – добуток незвідних множників
– добуток незвідних множників  з певною кратністю. Знаходимо похідну многочлена
з певною кратністю. Знаходимо похідну многочлена  , де
, де 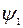 не ділиться на
не ділиться на  . Найбільший спільний дільник
. Найбільший спільний дільник  є добутком усіх множників, які входять у розклади як
є добутком усіх множників, які входять у розклади як  так і
так і  :
: 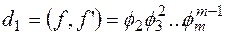
Знайдемо  , де
, де 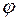 2 не ділиться на
2 не ділиться на 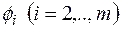
Далі  .
.
Аналогічно 
...........................................


тут  (і = 1,...,m) не містять множників
(і = 1,...,m) не містять множників  . Тепер треба знайти кожен множник
. Тепер треба знайти кожен множник  окремо, тому поділимо
окремо, тому поділимо  на
на  , отримаємо:
, отримаємо:


......................................


звідси маємо формули для  :
: 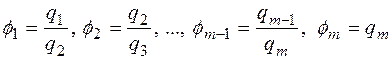 .
.
Приклад. Алгоритм відокремлення кратних множників:
 .
.
Знаходимо похідну многочлена  :
:

За алгоритмом Евкліда знаходимо НДС многочленів 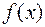 і
і 
x3 - 3x2 + 4 |3x2 - 6x 3x2 - 6x |-6x + 12
3x3 - 9x2 + 12 |x - 1 6x2 - 12x | -x
3x3 - 6x2 6x2 - 12x
_ - 3x2 + 12 0
- 3x2 + 6x
-6x + 12
НДС = 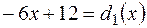
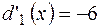


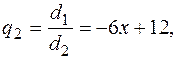

x3 - 3x2 + 4 |-6x + 12 x2 - x - 2 |-6x + 12
6x3 + 18x2 - 24 |x2 - x - 2 -6x2 + 6x + 12 |x + 1
6x3 + 12x2-6x2 + 12x
_ 6x2 - 24 -6x + 12
6x2 - 12x -6x + 12
12x - 24 0
12x - 24
Знаходимо 

Відповідь: 
ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ.
3.1. Довести, що многочлен 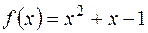 незвідний в
незвідний в 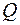 .
.
Розв’язання.
Многочлен  є звідним у полі
є звідним у полі 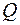 , якщо його можна розкласти в добуток не менше як двох многочленів ненульового степеня з кільця
, якщо його можна розкласти в добуток не менше як двох многочленів ненульового степеня з кільця 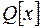 .
.
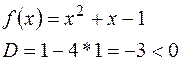
коренів немає, тому в полі 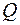 цей многочлен незвідний.
цей многочлен незвідний.
3.2.Розкласти многочлен  на незвідні множники в полі
на незвідні множники в полі  , якщо відомо, що цей многочлен має два корені, які є протилежними елементами в
, якщо відомо, що цей многочлен має два корені, які є протилежними елементами в  .
.
Розв’язання.
В  є такі елементи :
є такі елементи :  . Протилежними коренями є
. Протилежними коренями є  .
.
Так, як  - многочлен третього степеня, то
- многочлен третього степеня, то

Прирівнюємо відповідні коефіцієнти:
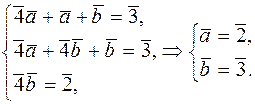
тому  .
.
3.3. Розкласти на незвідні множники в полі  многочлен
многочлен  , якщо
, якщо 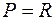 .
.
Розв’язання.
Це симетричний многочлен, тому винесемо за дужки  :
:

Нехай  , тоді
, тоді 

3.4. Знайти кратність кореня  многочлена
многочлена 
з кільця 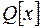 .
.
Розв’язання.
Для цього використаємо схему Горнера:
| -6 | -6 | ||||
| -3 | -3 | ||||
 - корінь кратності 2
- корінь кратності 2
3.5.Відокремити кратні кoрені многочлена  .
.
Розв’язання.
Знаходимо похідну многочлена f(x) і шукаємо їх НСД:

x5 -ix4 + 5x3 - ix2 + 8x + 4i | 5x4 - 4ix4 + 15x3 - 2ix + 8
5x5 - 5ix4 + 25x3 - 5ix2 + 40x + 20i | x - i
5x5 - 4ix4 + 15x3 - 2ix + 8x
-ix4 + 10x3 - 3ix2 + 32x + 20i
-5ix4 + 50x3 - 15ix2 + 160x + 100i
-5ix4 - 4x3 - 15ix2 - 2x - 8i
54x3 + 162x + 108i
5x4 - 4ix4 + 15x3 - 2ix + 8 | x3 + 3x + 2i
5x4 + 15x2 + 10ix | 5x - 4i
-4ix3 - 12ix + 8
-4ix3 - 12ix + 8
Отже

x3 + 3x + 2 | 3x2 + 3 3x2 + 3 | 6x + 6i
3x3 + 9x + 6i | x x2 + 1 | x + i
3x3 + 3xx2 + ix | x - i
6x + 6i -ix + 1
-ix + 1
Знаходимо 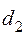 :
: 
3x2 + 3 | 6x + 6i
x2 + 1 | x + i
x2 + ix | x - i
_-ix + 1
-ix + 1

обчислимо многочлени 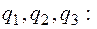


x5 - ix4 + 5x3 - ix2 + 8x + 4i | x3 + 3х + 2ix3 + 3x + 2i | x + i
x5 + 3x3 + 2ix2 | x2 - ix + 2 x3 + ix2 | x2 - ix + 2
-ix4 + 2x3 - 3ix2 + 8x + 4i -ix2 + 3x + i2
-ix4 - 3ix2 + 2x-ix2 + x
2x3 + 6x + 4i 2x + 2i
2x3 + 6x + 4i2x + 2i
0 0

x2 – ix + 2 | x + i
x2 + ix | x + 2i
-2ix + 2
-2ix +2
Тепер знайдемо  .
.
Таким чином маємо:  .
.
3.6.Довести, що многочлен  звідний у полі Z.
звідний у полі Z.
Розв’язання.
Якщо многочлен звідний у полі Z, то його можна розкласти на добуток не менше як двох многочленів ненульового степеня з
кільця Z[x].
Щоб розкласти многочлен  на множники, застосуємо метод невизначених коефіцієнтів. При цьому розглянемо єдиний випадок можливого розкладу: один множник першого степеня, а другий другого степеня.
на множники, застосуємо метод невизначених коефіцієнтів. При цьому розглянемо єдиний випадок можливого розкладу: один множник першого степеня, а другий другого степеня.
Нехай  .
.
Тоді з рівності 
маємо систему:

Розв¢язуючи цю систему з першого рівняння маємо, що  , а з останнього:
, а з останнього:  або
або  . Розглянемо кожну з чотирьох отриманих систем:
. Розглянемо кожну з чотирьох отриманих систем:
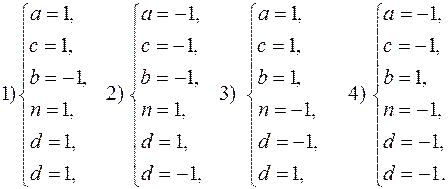
Бачимо, що сумісними є дві системи: 1) і 4), тому маємо два розв¢язки:  або
або  .
.
3.7.Розкласти многочлен  за степенями двочлена
за степенями двочлена 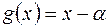 і знайти
і знайти  , якщо
, якщо  належить Q[x] і a = 1.
належить Q[x] і a = 1.
Розв’язання.
I спосіб. Знаходимо похідні многочлена  :
:

Тоді

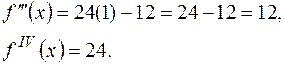
Щоб знайти розклад многочлена  за степенями двочлена
за степенями двочлена 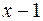 , застосуємо формулу Тейлора, яка справджується для многочленів над полем характеристики 0:
, застосуємо формулу Тейлора, яка справджується для многочленів над полем характеристики 0:

Оскільки  то
то 
ІІ спосіб. Знайдемо розклад многочлена  за степенями двочлена
за степенями двочлена  , застосувавши для знаходження коефіцієнтів розкладу схему Горнера:
, застосувавши для знаходження коефіцієнтів розкладу схему Горнера:
| -2 | -5 | ||||
| -1 | -3 | -2= 
| |||
-1= 
| |||||
3= 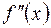
| |||||
2= 
| |||||
1= 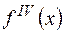
|

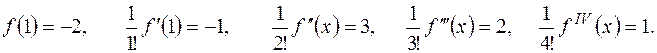
Отже, 
