 |
|
Розділ V. Цікаві задачки
Задачі на доведення
15.1. Довести, що якщо 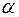 і
і 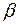 - корені многочлена
- корені многочлена 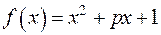 , а
, а  і
і 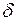 - корені многочлена
- корені многочлена 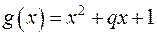 , то виконується рівність
, то виконується рівність 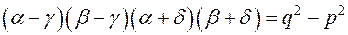 .
.
Доведення.
За теоремою Вієта маємо: 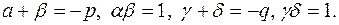 Звідси:
Звідси:
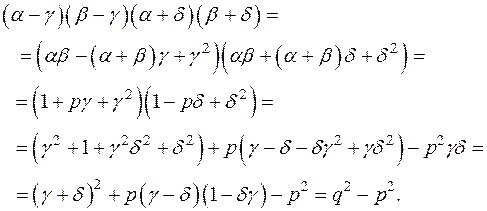
15.2. Довести, що 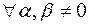 корені
корені 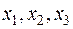 многочлена
многочлена  задовольняють рівність
задовольняють рівність

Доведення.
За теоремою Вієта маємо: 
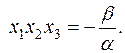 Тому:
Тому:
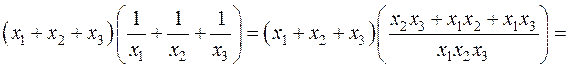
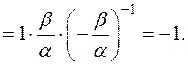
15.3. Довести, що 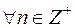 многочлен
многочлен  ділиться на многочлен
ділиться на многочлен  .
.
Доведення.
Використаємо метод математичної індукції:
1. 
2. припустимо, що 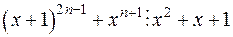 , тоді:
, тоді:
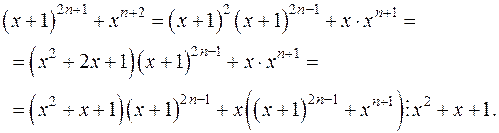
15.4 Довести, що 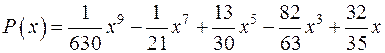 при
при 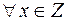 набуває цілих значень.
набуває цілих значень.
Доведення.
Запишемо цей многочлен у вигляді
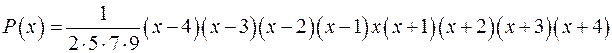 .
.
Оскільки серед дев’яти послідовних цілих чисел завжди знайдуться ті, що діляться
націло на 2, 5, 7, 9, тому 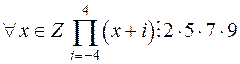 (добуток взаємно простих чисел). Отже, многочлен
(добуток взаємно простих чисел). Отже, многочлен 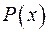 набуває цілих значень.
набуває цілих значень.
15.5. Для заданих 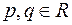 знайти всі значення, які многочлен
знайти всі значення, які многочлен 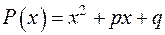 набуває при
набуває при  .
.
Розв’язання.
Функція 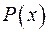 має на графіку одну точку мінімуму
має на графіку одну точку мінімуму 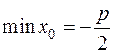 . При
. При 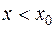 функція спадає, а при
функція спадає, а при 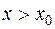 - зростає. Тому для множини
- зростає. Тому для множини 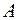 значень даної функції
значень даної функції 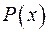 на
на 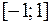 маємо: якщо
маємо: якщо  , то
, то
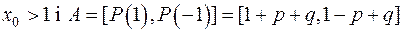 ; якщо
; якщо  , то
, то
 , тобто
, тобто  , при
, при  , при
, при 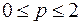 ; якщо
; якщо 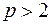 , то
, то

15.6. Довести, що 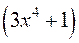 сумою трьох квадратів.
сумою трьох квадратів.
Доведення.
Додамо і віднімемо вираз  :
:
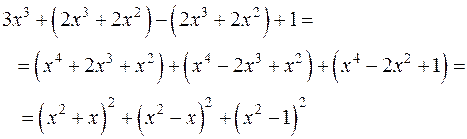
що і треба було довести.
15.7. Довести, що якщо 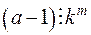 , то
, то  .
.
Доведення.

Так як 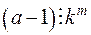 , то кожний з доданків, що стоять в квадратних дужках, включаючи
, то кожний з доданків, що стоять в квадратних дужках, включаючи 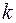 , напевно діляться на
, напевно діляться на 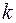 . Отже, права частина рівності, ф одночасно й
. Отже, права частина рівності, ф одночасно й 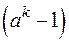 , діляться на
, діляться на  .
.
15.8. Довести, що корені рівняння  дійсні числа, якщо
дійсні числа, якщо  .
.
Доведення.
Після деяких перетворень маємо

15.9. Довести теорему: якщо 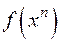 ділиться на
ділиться на 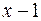 , то ділиться також і на
, то ділиться також і на  .
.
Доведення.
Якщо 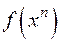 ділиться на
ділиться на 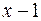 , то
, то 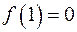 і, отже,
і, отже, 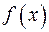 ділиться на
ділиться на 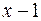 , звідки випливає, що
, звідки випливає, що 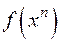 ділиться на
ділиться на  .
.
15.10. Довести, що многочлен третього степеня незвідний, якщо він не має раціональних коренів.
Доведення
Звідний многочлен третього степеня має множник першого степеня з раціональними коефіцієнтами, том він має раціональний корінь.
15.11. Знайти необхідні і достатні умови незвідності многочлена 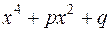 з раціональними (можуть бути дробовими) коефіцієнтами.
з раціональними (можуть бути дробовими) коефіцієнтами.
Доведення.
Без порушення загальності можна шукати умови, при яких 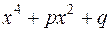 розкладається на множники другого степеня з раціональними коефіцієнтами, бо якщо многочлен має раціональний корінь
розкладається на множники другого степеня з раціональними коефіцієнтами, бо якщо многочлен має раціональний корінь 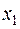 , то
, то 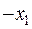 буде також раціональним коренем і лінійні множники, які їм відповідають можна об’єднати.
буде також раціональним коренем і лінійні множники, які їм відповідають можна об’єднати.
Нехай  .
.
Тоді 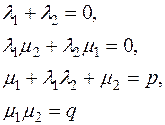
Якщо  , то і
, то і 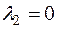 . У цьому випадку для існування раціональних
. У цьому випадку для існування раціональних  і
і  необхідно і достатньо, щоб дискримінант
необхідно і достатньо, щоб дискримінант  був квадратом раціонального числа.
був квадратом раціонального числа.
Нехай 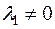 , тоді
, тоді 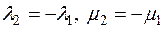 , і далі
, і далі 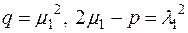 . Отже для звідності многочлена
. Отже для звідності многочлена 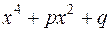 необхідно і достатньо виконання однієї з двох умов:
необхідно і достатньо виконання однієї з двох умов:
1)  є квадратом раціонального числа;
є квадратом раціонального числа;
2)  є квадратом раціонального числа
є квадратом раціонального числа 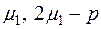 є квадрат раціонального числа
є квадрат раціонального числа 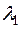 .
.
15.12. Довести, що корені многочлена 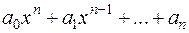 з дійсними або комплексними коефіцієнтами не перевищують по модулю:
з дійсними або комплексними коефіцієнтами не перевищують по модулю: 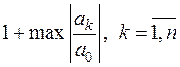 .
.
Доведення
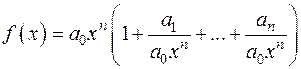 . Нехай
. Нехай 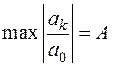 . Тоді при
. Тоді при
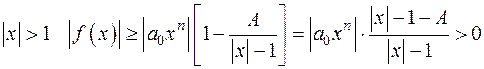 при
при 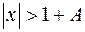 .
.
15.13. Довести, що якщо ряд Штурма містить многочлени всіх степенів від нульового до  -го, до число змін знаку в ряді старших коефіцієнтів многочленів Штурма дорівнюють кількості пар спряжених комплексних коефіцієнтів даного многочлена.
-го, до число змін знаку в ряді старших коефіцієнтів многочленів Штурма дорівнюють кількості пар спряжених комплексних коефіцієнтів даного многочлена.
Доведення
Нехай 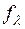 і
і 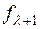 два сусідніх многочлена „повного” ряду Штурма. Якщо їх старші
два сусідніх многочлена „повного” ряду Штурма. Якщо їх старші
коефіцієнти мають однакові знаки, то їх значення при 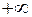 не утворюють зміни знаку, а значення при
не утворюють зміни знаку, а значення при 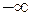 дають зміну знаку, так як степінь одного з многочленів парний, а степінь другого – не парний. Якщо ж старші коефіцієнти мають протилежні знаки, то значення
дають зміну знаку, так як степінь одного з многочленів парний, а степінь другого – не парний. Якщо ж старші коефіцієнти мають протилежні знаки, то значення 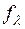 і
і 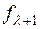 при
при 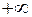 дають зміну знаку, а при
дають зміну знаку, а при 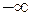 - не дають. Тому, позначивши через
- не дають. Тому, позначивши через 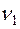 та
та 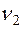 число змін знаку в ряді Штурма при
число змін знаку в ряді Штурма при 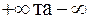 , маємо, що
, маємо, що  . З іншого боку,
. З іншого боку,  дорівнює числу
дорівнює числу  дійсних коренів многочлена. Отже.
дійсних коренів многочлена. Отже. 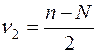 , що і треба було довести.
, що і треба було довести.
15.14. Довести, що якщо 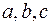 - сторони трикутника, то корені рівняння
- сторони трикутника, то корені рівняння 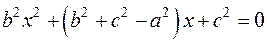 уявні.
уявні.
Доведення.
За умовою  . Квадратне рівняння має уявні корені тоді і тільки тоді, коли його дискримінант від’ємний
. Квадратне рівняння має уявні корені тоді і тільки тоді, коли його дискримінант від’ємний 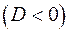 . Знайдемо його:
. Знайдемо його:
 Так як сума двох сторін трикутника більша за третю, то вирази в перших трьох дужках додатні
Так як сума двох сторін трикутника більша за третю, то вирази в перших трьох дужках додатні 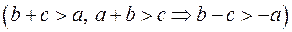 , а четвертих дужках вираз від’ємний. Отже,
, а четвертих дужках вираз від’ємний. Отже, 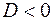 і корені даного рівняння уявні.
і корені даного рівняння уявні.
§ 16. Нестандартні задачі
16.1. Знайти всі значення  , при яких корені
, при яких корені 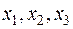 многочлена
многочлена 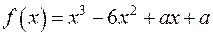 задовольняють рівність
задовольняють рівність 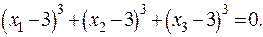
Розв’язання.
Введемо заміну 
Тоді числа  є коренями многочлена
є коренями многочлена
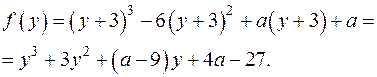
За теоремою Вієта:
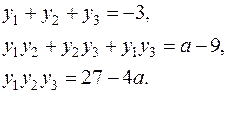
Справедлива тотожність:
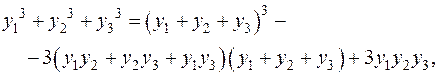
з якої отримуємо необхідну і достатню умову для  :
:
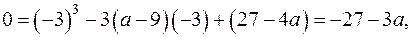 тобто
тобто 
16.2. Знайти всі многочлени 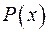 з дійсними коефіцієнтами, для яких при всіх дійсних значеннях
з дійсними коефіцієнтами, для яких при всіх дійсних значеннях  одночасно виконуються дві нерівності:
одночасно виконуються дві нерівності:
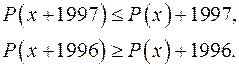
Розв’язання.
Розглянемо многочлен  Він обмежений при
Він обмежений при 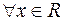 числом 1997, тому
числом 1997, тому 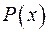 - лінійний многочлен,
- лінійний многочлен, 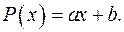 Отже, має бути
Отже, має бути  звідки
звідки 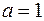 . Тому
. Тому 
16.3. Знайти ненульові многочлени 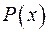 такі, що
такі, що 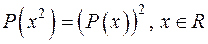 .
.
Розв’язання.
Нехай  . Припустимо,що хоча б один з
. Припустимо,що хоча б один з  відмінний від нуля. Виберемо
відмінний від нуля. Виберемо
 де
де 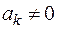 .
.
Тоді 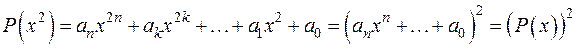 .
.
Прирівнюючи коефіцієнти при  , отримаємо
, отримаємо 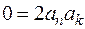 , яке протирічить умові
, яке протирічить умові 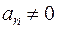 ,
, 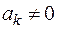 . Отже,
. Отже, 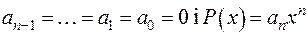 . За умовою
. За умовою  отримуємо, що
отримуємо, що 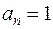 . Тому
. Тому 
16.4. Знайти ненульові многочлени 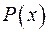 такі, що
такі, що 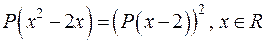 .
.
Розв’язання.
Позначимо  Тоді маємо
Тоді маємо
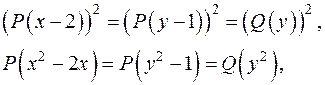
а початкова тотожність записується як 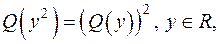 тобто з точністю до позначень співпадає з тотожністю з попередньої задачі. Тому
тобто з точністю до позначень співпадає з тотожністю з попередньої задачі. Тому 
16.5. Знайти всі дійсні функції  такі, що
такі, що 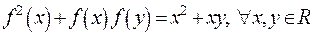 .
.
Розв’язання.
При  буде
буде 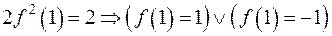 . Підставляємо тепер
. Підставляємо тепер 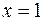 : в першому випадку
: в першому випадку  , в другому -
, в другому - 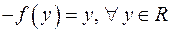 . Перевіркою переконуємося, що обидві функції підходять. Отже,
. Перевіркою переконуємося, що обидві функції підходять. Отже, 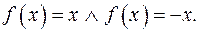
16.6. Для заданих 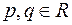 знайти всі значення, які многочлен
знайти всі значення, які многочлен 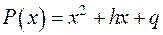 набуває при
набуває при  .
.
Розв’язання.
Функція 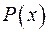 має на графіку одну точку мінімуму
має на графіку одну точку мінімуму 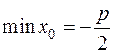 . При
. При 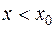 функція спадає, а при
функція спадає, а при 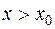 - зростає. Тому для множини
- зростає. Тому для множини 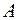 значень даної функції
значень даної функції 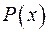 на
на 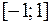 маємо: якщо
маємо: якщо  , то
, то 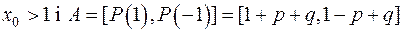 ; якщо
; якщо  , то
, то
 , тобто
, тобто  , при
, при  , при
, при 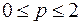 ; якщо
; якщо 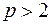 , то
, то
 .
.
16.7. Представити у вигляді двох квадратів многочлен 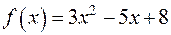 .
.
Розв’язання.
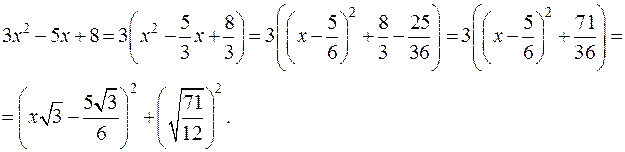
16.8. Розкласти на множники многочлен  .
.
Розв’язання.
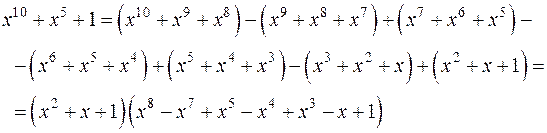
16.9. Скласти рівняння за його коренями 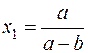 ,
,  .
.
Розв’язання.
Коефіцієнт при першому степені невідомого рівний
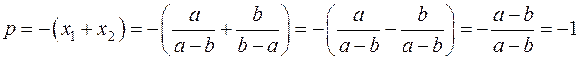 .
.
Вільний член рівний 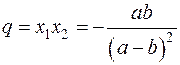 .
.
Шукане рівняння має вигляд  .
.
16.10. 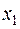 і
і 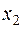 - корені рівняння
- корені рівняння 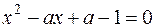 . Знайти
. Знайти 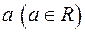 , щоб величина
, щоб величина 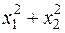 була мінімальною.
була мінімальною.
Розв’язання.
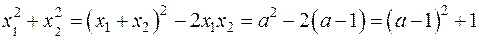 .
.
Отриманий вираз матиме мінімальне значення при 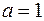 .
.
16.11. Розв’язати рівняння  .
.
Розв’язання.
Заміна

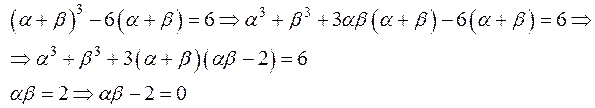
Маємо 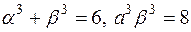 . Тому
. Тому 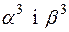 коефіцієнти рівняння
коефіцієнти рівняння 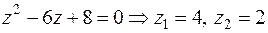 .
.
Тоді
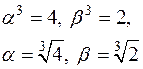 .
.
Отже  .
.
16.12. Визначити число дійсних коренів многочлена 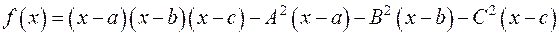 , якщо
, якщо 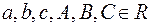 .
.
Розв’язання.
Для цього треба знайти  . Нехай
. Нехай
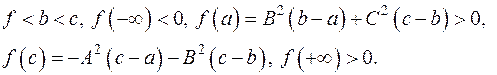
Отже, 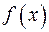 має дійсні корені в проміжках
має дійсні корені в проміжках 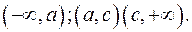
§ 17. Задачі для самостійного розв’язання
1) Знайти всі дійсні розв’язки рівняння 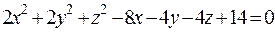
2) Нехай  і
і  два з чотирьох коренів многочлена
два з чотирьох коренів многочлена 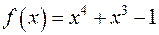 . Довести, що
. Довести, що  – корінь многочлена
– корінь многочлена 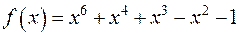 .
.
3) Дано  має два різних кореня на проміжку
має два різних кореня на проміжку  . Довести, що
. Довести, що 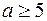 . Знайти, хоча б одну пару
. Знайти, хоча б одну пару  і
і  при
при  .
.
4) Знайти многочлени 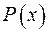 такі, що
такі, що 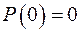 і
і 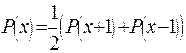
5) Знайти всі 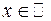 при яких многочлен
при яких многочлен 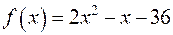 набувають значень, рівних квадратам простих чисел.
набувають значень, рівних квадратам простих чисел.
6) Довести, що дана система не має розв’язку у полі цілих чисел 
7) Розкласти на множники многочлен 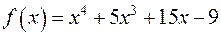 .
.
8) Рівняння 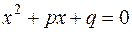 з раціональними коефіцієнтами має корінь
з раціональними коефіцієнтами має корінь 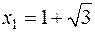 . Знайти другий корінь рівняння.
. Знайти другий корінь рівняння.
9) Довести, що корені рівняння 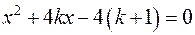 при
при 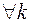 - дійсні числа. З’ясувати знаки коренів.
- дійсні числа. З’ясувати знаки коренів.
10) Довести, що якщо  , то
, то 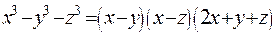 .
.
11) Розв’язати рівняння 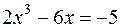 .
.
12) Розв’язати в полі натуральних чисел 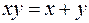 .
.
Словничок термінів
А
Алгебраїчна рівність многочленів – див. рівність многочленів.
Алгебраїчним розширенням поля Р називається розширення 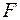 поля
поля  , якщо всі його елементи є алгебраїчними відносно поля Р.
, якщо всі його елементи є алгебраїчними відносно поля Р.
Алгебраїчним числом відносно поля Р називається число α, якщо воно є коренем деякого многочлена над полем  .
.
Алгебраїчно замкненимназивається поле  , яке є полем розкладу будь-якого многочлена
, яке є полем розкладу будь-якого многочлена  .
.
Алгоритм Евкліда:
маємо многочлени  і
і  , причому deg
, причому deg 
 deg
deg  . Виконаємо послідовне ділення:
. Виконаємо послідовне ділення:
 =
= 
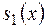 +
+ 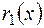
 =
= 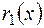
 +
+ 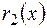
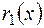 =
= 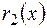
 +
+ 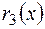
…
 =
= 
 +
+ 
 =
= 

Остання відмінна від нуля остача у цій системі рівностей 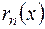 і є НСД многочленів
і є НСД многочленів  і
і  .
.
Асоційованими називаються многочлени  і
і  з кільці
з кільці 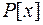 , якщо вони відрізняються лише множником, який є відмінною від нуля константою:
, якщо вони відрізняються лише множником, який є відмінною від нуля константою: 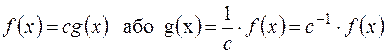 ).
).
В
Взаємно простими називаються многочлени  і
і 

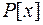 , якщо їх спільний дільник є многочлен нульового степеня: (
, якщо їх спільний дільник є многочлен нульового степеня: (  ,
,  ) = 1.
) = 1.
Вільним (нульовим) членом многочлена  називається елемент
називається елемент 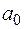 .
.
Д
Ділення націло:многочлен  ділиться націло на
ділиться націло на 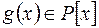
( записується 

 ), якщо існує многочлен
), якщо існує многочлен 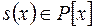 такий, що
такий, що
 .
.
Дискримінантом  многочлена
многочлена  називається вираз
називається вираз 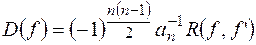 , де
, де 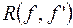 - результант
- результант  і його похідної
і його похідної  .
.
· При цьому справджується рівність:  ,
,
де  корені
корені  .
.
Дискримінантом рівняння третього степеня з комплексними коефіцієнтами  , яке за допомогою підстановки
, яке за допомогою підстановки  зводиться до виду
зводиться до виду 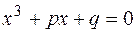 , називається число
, називається число  .
.
Добутком многочленів 
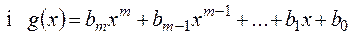
називається многочлен  , де
, де 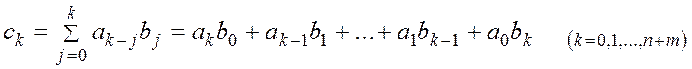 ,
,  , тобто
, тобто  .
.
Е
Елементарним дробом у полі Р називається раціональний дріб
виду  , де
, де  - незвідний многочлен у полі Р,
- незвідний многочлен у полі Р,  і
і  , а
, а 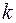 – будь-яке натуральне число.
– будь-яке натуральне число.
З
Звідним (складеним) у полі Р називається многочлен
 , якщо deg f
, якщо deg f  1 і в кільці Р[x] існують многочлени f(x) i g(x), такі, що
1 і в кільці Р[x] існують многочлени f(x) i g(x), такі, що  i
i  , такі, що
, такі, що
 =
= 
 , deg g
, deg g  1 і deg s
1 і deg s  1.
1.
Звідним у полі Р називається многочлен від n змінних  , якщо
, якщо  і
і 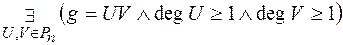 .
.
Значенням многочлена 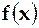 при
при 
 R,називається елемент
R,називається елемент  з кільця R і позначається
з кільця R і позначається  , якщо многочлен
, якщо многочлен 
 R[x] має канонічну форму.
R[x] має канонічну форму.
І
Інтерполяційним многочленом Лагранжа називають многочлен виду:
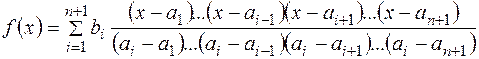 (1)
(1)
Нехай  – деяке поле,
– деяке поле,  - різні елементи поля
- різні елементи поля  і
і  - довільні елементи поля
- довільні елементи поля  . Існує один і тільки один многочлен
. Існує один і тільки один многочлен  в кільці
в кільці  [x], степінь якого не перевищує
[x], степінь якого не перевищує  і який набуває в (
і який набуває в (  )-й точці
)-й точці  задані значення
задані значення 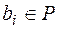 ,
, 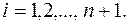
Шуканий многочлен має вигляд (1).
Інтерполяційним многочленом Ньютонаназивають многочлен виду:
 (2)
(2)
Іноді доцільно многочлен (1) записувати у вигляді (2), де коефіцієнти  визначаються послідовним підставленням значень
визначаються послідовним підставленням значень  .
.
К
Канонічним розкладом многочлена  у полі Р[x]називається подання довільного многочлена ненульового степеня над полем
у полі Р[x]називається подання довільного многочлена ненульового степеня над полем 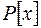 у вигляді
у вигляді 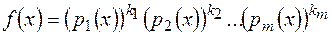 , де
, де 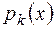 – попарно різні (неасоційовні) многочлени, незвідні у полі Р[x]. Це зображення єдине з точністю до сталих множників і їх нумерації.
– попарно різні (неасоційовні) многочлени, незвідні у полі Р[x]. Це зображення єдине з точністю до сталих множників і їх нумерації.
Канонічною формою многочлена f (x) називається упорядкування його членів за спаданням степеня  .
.
Квадратичним розширенням поля Рназивається просте алгебраїчне розширенням 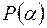 , утворене з поля
, утворене з поля  приєднанням до нього числа α, яке є коренем квадратного тричлена над полем
приєднанням до нього числа α, яке є коренем квадратного тричлена над полем  і не належить полю
і не належить полю  .
.
k-тим членом або членом k-го степеня многочлена  називається вираз
називається вираз  (к =
(к =  ).
).
Кількістю змін знаків даної послідовності називається кількість пар сусідніх чисел деякої впорядкованої послідовності дійсних чисел  , які мають протилежні знаки.
, які мають протилежні знаки.
Кільцем многочленів 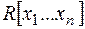 від
від  змінних
змінних  над областю цілісності Rназивається кільце многочленів від однієї змінної
над областю цілісності Rназивається кільце многочленів від однієї змінної 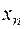 над кільцем
над кільцем 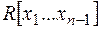 , тобто
, тобто 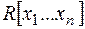 =
= 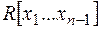
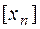 .
.
Коефіцієнтом k-го члена  многочлена
многочлена  від
від
n змінних є елемент 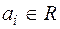 .
.
Коренем многочлена f (х)називається число  , якщо
, якщо  = 0.
= 0.
Кратним множником називають множник, кратність якого більша за 1. Якщо многочлен 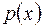 входить у канонічний розклад у степені з показником
входить у канонічний розклад у степені з показником  , то кажуть, що
, то кажуть, що  є множником кратності
є множником кратності  многочлена
многочлена  .
.
Кратний корінь– це корінь, кратність якого більша за 1.
Л
Лінійним представленням НСД є запис виду: 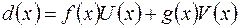 ,
,
де 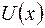 і
і  – деякі многочлени з
– деякі многочлени з  [x], а
[x], а 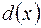 - НСД двох многочленів
- НСД двох многочленів
 i
i 

 [x].
[x].
Лексикографічним записомназивається відношення “бути вищим” на множині членів многочленів, що є лінійним строгим порядком.
Нехай  і
і 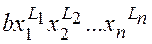 - два члени многочлена
- два члени многочлена  .Вважається, що перший елемент вищий від другого, якщо
.Вважається, що перший елемент вищий від другого, якщо  (позначають
(позначають 

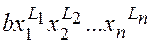 ).
).
М
Мінімальним полем Р{M}, що містить дану числову множину М, називається поле, яке є перетином усіх числових полів, що містять
множину М.
Многочленом (поліномом) від однієї змінної над областю цілісності R називається вираз виду
 , де
, де
 - довільне ціле невід’ємне число,
- довільне ціле невід’ємне число,
 – елементи R,
– елементи R,
 – деякі символи;
– деякі символи;
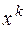 - k-ий степінь змінної
- k-ий степінь змінної  ,
,
 - k-ий коефіцієнт многочлена або коефіцієнт при
- k-ий коефіцієнт многочлена або коефіцієнт при  (k=
(k=  ).
).
Многочленом від  змінних над
змінних над 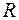 називаєтьсякожний елемент кільця
називаєтьсякожний елемент кільця 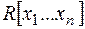 і позначається
і позначається  ,
,  і т.д.
і т.д.
Н
Найменшим спільним кратним (НСК) многочленів f(x) і g(x) називається їх спільне кратне, на яке ділиться кожне спільне кратне цих многочленів. Позначається так: [ 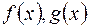 ].
].
Найбільшим спільним дільником (НСД) називається спільний дільник многочленів  і
і  , який ділиться на кожен інший спільний дільник
, який ділиться на кожен інший спільний дільник  і
і  і позначається (
і позначається ( 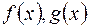 ).
).
Незвідним (нерозкладним, простим) називається многочлен  , якщо він не є константа і не має дільників, відмінних від константи і від многочлена виду
, якщо він не є константа і не має дільників, відмінних від константи і від многочлена виду  , де
, де  - константа.
- константа.
Незвідним у полі Р називається многочлен  від
від  змінних, якщо
змінних, якщо  і
і  .
.
Неправильним називається раціональний дріб  , якщо степінь
, якщо степінь  більша за степінь
більша за степінь  .
.
Нуль - многочленом над R називають елемент 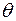
 R, який вважаємо константою і многочленом, і позначаємо
R, який вважаємо константою і многочленом, і позначаємо  , тобто
, тобто
 = 0.
= 0.
О
Область цілісності – це комутативне кільце з 1 без дільників нуля ( R[x] - сукупність всіх многочленів над областю цілісності ).
Однорідним називається многочлен у якого всі члени многочлена мають однакову степінь.
П
Подібними називаються два члени многочлена, які відрізняються тільки коефіцієнтами.
Полем розкладу многочленаназивається поле  , де
, де  розкладається на лінійні множники.
розкладається на лінійні множники.
Полем розкладу многочлена  від n зміннихназивається поле Р, якщо
від n зміннихназивається поле Р, якщо  розкладається в
розкладається в 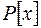 на лінійні множники.
на лінійні множники.
Похідною від многочлена 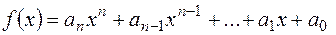 називається многочлен
називається многочлен 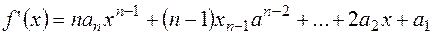 . Похідна від нуль - многочлена дорівнює нулю.
. Похідна від нуль - многочлена дорівнює нулю.
Правильним називається раціональний дріб  , якщо степінь
, якщо степінь  менша за степінь
менша за степінь  .
.
Примітивним (відносно S) називається многочлен 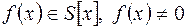 , якщо НСД його коефіцієнтів дорівнює одиниці.
, якщо НСД його коефіцієнтів дорівнює одиниці.
Простим алгебраїчним (трансцендентним) розширенням поля Рназивається поле 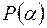 , утворене приєднанням до поля
, утворене приєднанням до поля  числа α, алгебраїчного (трансцендентного) відносно поля
числа α, алгебраїчного (трансцендентного) відносно поля  .
.
Простий многочлен див. незвідний многочлен.
Простими називаються корені кратності 1.
Р
Результантом многочленів  і
і  називається вираз виду
називається вираз виду
 , де
, де 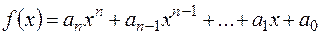 і
і 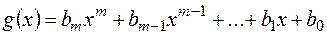 - многочлени над полем
- многочлени над полем  ,
,  і
і  - корені
- корені  .
.
Рівними між собою називаються многочлени  і
і  (
(  =
=  ), якщо їх канонічні форми збігаються : мають однакові степені і попарно рівні відповідні коефіцієнти ( алгебраїчна рівність многочленів).
), якщо їх канонічні форми збігаються : мають однакові степені і попарно рівні відповідні коефіцієнти ( алгебраїчна рівність многочленів).
Розклад  многочлена ненульового степеня над полем
многочлена ненульового степеня над полем 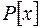 на незвідні множники у полі
на незвідні множники у полі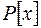 -це представлення його у вигляді
-це представлення його у вигляді 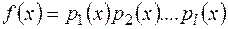 , де всі
, де всі 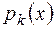 є незвідними многочленами у полі
є незвідними многочленами у полі 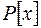 . Це зображення єдине з точністю до сталих множників і до порядку нумерації многочленів
. Це зображення єдине з точністю до сталих множників і до порядку нумерації многочленів 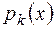 .
.
С
Симетричним відносно змінних  називається многочлен
називається многочлен  , якщо внаслідок довільної перестановки змінних
, якщо внаслідок довільної перестановки змінних  утворюється многочлен рівний даному.
утворюється многочлен рівний даному.
Скінченим розширенням поля P називається поле 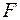 , якщо в ньому існує така лінійно незалежна відносно поля
, якщо в ньому існує така лінійно незалежна відносно поля  система елементів
система елементів 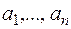 , що будь-який елемент
, що будь-який елемент  є лінійною комбінацією цих елементів з коефіцієнтами зполя
є лінійною комбінацією цих елементів з коефіцієнтами зполя  :
: 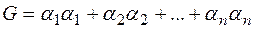 . Система
. Система 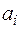 - базис поля
- базис поля 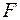 відносно поля
відносно поля  .
.
Складений многочлен – див. незвідний многочлен.
Складним розширенням поля Рназивається розширення 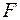 , якщо існує такий ланцюжок розширень
, якщо існує такий ланцюжок розширень 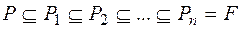 , що
, що  , причому кожне αi є алгебраїчним числом над полем
, причому кожне αi є алгебраїчним числом над полем  (при
(при  ).
).
Спільним кратним многочленів f(x) і g(x)  Р[x] називають будь-який многочлен
Р[x] називають будь-який многочлен 
 Р[x] такий, що
Р[x] такий, що 


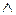


 .
.
Спільним дільником f(x) i g(x)називається многочлен 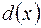 , який є дільником многочлена
, який є дільником многочлена  і многочлена
і многочлена  одночасно.
одночасно.
Старшим членом многочлена 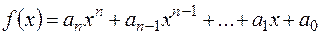 є відмінний від нуля член многочлена, степінь якого більший за степінь усіх інших, відмінних від нуля членів цього многочлена. його коефіцієнт – старшим коефіцієнтом многочлена, а його степінь – степенем многочлена.
є відмінний від нуля член многочлена, степінь якого більший за степінь усіх інших, відмінних від нуля членів цього многочлена. його коефіцієнт – старшим коефіцієнтом многочлена, а його степінь – степенем многочлена.
Степенем  члена многочлена від n змінних називається сума
члена многочлена від n змінних називається сума  . Число
. Число  називається степенем даного члена відносно
називається степенем даного члена відносно  . Найбільший із степенів членів називається степенем многочлена, а член з найбільшим степенем – старшим членом многочлена.
. Найбільший із степенів членів називається степенем многочлена, а член з найбільшим степенем – старшим членом многочлена.
Сумою многочленів
 називають многочлен
називають многочлен

Т
Трансцендентним відносно поля Рназивається число, яке не є алгебраїчним відносно поля  .
.
Ф
Функціональна рівність многочленів: кожен многочлен 
 R[x] визначає відображення jf = R®R таке, що jf (
R[x] визначає відображення jf = R®R таке, що jf (  ) =
) =  . Якщо область цілісності R має характеристику 0, то многочлени
. Якщо область цілісності R має характеристику 0, то многочлени  і
і  R[x] рівні тоді і тільки тоді, коли рівні функції jf і jg, які вони визначають.
R[x] рівні тоді і тільки тоді, коли рівні функції jf і jg, які вони визначають.
Ч
Членом многочлена  називається кожен доданок
називається кожен доданок  в су
в су