 |
|
Пропускна здатність окремих каналів системи M/M/v/L//S
Для послідовного зайняття каналів (система M/M/v/L//S) пропускна здатність і-го каналу дорівнює різниці інтенсивностей надлишкового навантаження для групи з (і-1) каналу та і каналів, як видно з рисунку 5.5.
 |
Рисунок 5.5. Обслуговування найпростішого потоку системою з послідовним зайняттям каналів
Інтенсивність надлишкового навантаження обчислюється за (5.8), тоді:
hі =Ri-1 - Ri = [Ei-1(L) - Ei(L)] (5.12)
E0(L) = 1
З (5.12) випливає. що пропускна здатність і-го каналу при послідовному занятті не залежить від кількості каналів системи, а залежить лише від номеру каналу та інтенсивності навантаження, що надходить.
Вигляд залежності пропускної здатності і-го каналу від номеру каналу для 10 канальної СМО приведений на рис. 5.6 (L = 9 Ерл).
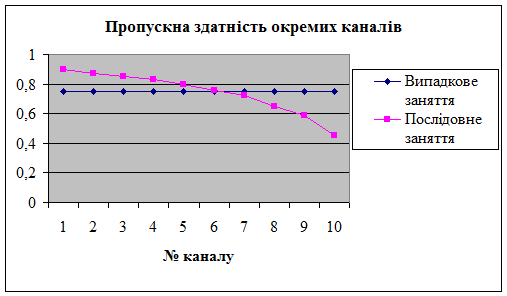
Рисунок 5.6. Пропускна здатність і-го каналу
Приклад 5.5
Визначити пропускну здатність першого каналу при випадковому и послідовному занятті каналів в системі M/M/4/L. l= 180 викл/год, h = 20c.
Рішення
Спочатку знаходимо інтенсивність навантаження, що надходить:
L = l* h = 180/60 викл/хв. * 1/3 хв = 1 Ерл
Пропускну здатність першого каналу при випадковому занятті каналів визначаємо за (5.11). Для чого спочатку розрахуємо E4(L)
E4(1) = (14/4!)/( 10/0! + 11/1! + 12/2! + 13/3! + 14/4!) = 1/24/(1+1+1/2+1/6+1/24)= = 0,042/2,71 = 0,015
Тоді, h1 = Y/4= 1[1-0,015]/4 = 0,246 (Ерл)
Пропускну здатність першого каналу при послідовному занятті каналів визначаємо за (5.11). Для чого спочатку розрахуємо E1(L), адже (E0(L) = 1):
E1(1) = (11/1!)/( 10/0! + 11/1!) = 0,5
h1 = 1*(1 – 0,5) = 0,5 (Ерл)
Таким чином пропускна здатність першого каналу при послідовному занятті каналів більше, ніж при випадковому.
Взагалі пропускна здатність першого каналу при послідовному занятті каналів і інтенсивності навантаження, що надходить, 1 Ерл, завжди дорівнює 0,5 Ерл.
Приклад 5.6
В системі М/М/40/L//R в середньому зайнято 30 каналів. Визначити пропускну здатність одного каналу.
Рішення
Оскільки при випадковому занятті пропускна здатність одного каналу (5.11) дорівнює Y/v, а за умовою задачі Y = 30 Ерл (середня кількість зайнятих каналів і є інтенсивність обслугованого навантаження), то h = 30/40 = 0,75 Ерл
5.5 Система Mr/M/V/L
5.5.1 Розподіл імовірностей станів системи Mr/M/V/L
Розглянемо більш складний випадок обслуговування системою з втратами потоку з простою післядією, тобто систему Mr/M/v/L.
Розглядається така математична модель. На v-канальну систему надходить потік викликів із простою післядією. Час обслуговування одного виклику – випадкова величина, розподілена за експоненціальним законом із середнім значенням, прийнятим за одиницю часу (h=1 у.о.ч.). Дисципліна обслуговування - з явними втратами повідомлень. Число зайнятих каналів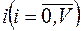 
назвемо станом досліджуваної системи. Параметр потоку викликів 
виражений у викл/у.о.ч. (Ерл); його можна також трактувати як інтенсивність вхідного навантаження у стані системи i, тоді інтенсивність потоку звільнення дорівнює числу зайнятих каналів i. При надходженні виклику або закінченні його обслуговування система стрибкоподібно переходить з одного стану в інший (рис.5.7). Припустимо, що в момент часу t = 0 відомий стан i системи, або розподіл імовірностей станів Pi(0).
Виникає задача: знайти розподіл імовірностей Pi(t) в момент t.
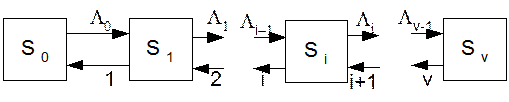
Рисунок 5.7. Граф станів системи Mr/M/v/L
Результат випливає з рішення системи диференційних рівнянь
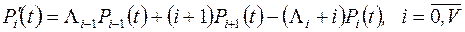(5.13)
Імовірності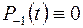 
та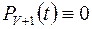 
як імовірності неіснуючих станів.
Система рівнянь (5.13) описує перехідний режим роботи досліджуваної системи обслуговування. Імовірності Pi(t), що є рішенням системи рівнянь (5.13), залежать від початкових умов, тобто від розподілу Рi(0). Проте для більшості практичних задач можна обмежитися дослідженням усталеного режиму, що досягається системою обслуговування при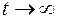 
.
При цьому імовірності Pi(t)® lim = const, які не залежить від t та початкового розподілу Pi(0). Відповідно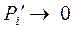 
. Система (5.13), як було показано в розділі 4, перетворюється в лінійну систему однорідних рівнянь:
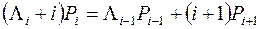(5.14)
Граничний розподіл імовірності Pi характеризує роботу системи обслуговування в стані статистичної рівноваги. В цих умовах в системі обслуговування, як і раніше, відбуваються випадкові зміни, проте імовірності, що описують поведінку СМО, не змінюються з часом. Систему (5.14) можна одержати безпосередньо, якщо скористатися таким правилом (п. 4.3), справедливим для стану статистичної рівноваги: сума інтенсивностей виходу зі стану системи i, зважена імовірністю Рi, дорівнює сумі зважених імовірностями відповідних станів інтенсивностей входу в цей стан.
Позначимо через
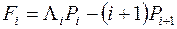, (5.15)
тоді з (5.14):
.
Звідси одержуємо просте рекурентне співвідношення для обчислення імовірностей Pi:
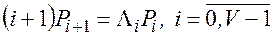. (5.16)
Задаючи значення i, рівними 0, 1, 2, ... , одержуємо:
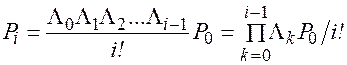(5.17)
Для визначення Р0 скористаємося умовою нормування:
.
Тоді
, (5.18)
і остаточно:
, 
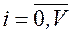. (5.19)
Формула (5.19) виражає розподіл імовірностей для усталеного режиму. Вона визначає імовірність зайнятості в довільний момент i каналів системи, яка обслуговує з явними втратами потік викликів із простою післядією. Імовірність Рi можна трактувати як частку часу, протягом якої в досліджуваній системі зайнято i виходів.
5.5.2 Основні випадки розподілу станів системи Mr/M/V/L
1. Потік викликів примітивний із параметром
дисципліна обслуговування з явними втратами. Тобто маємо систему Mi/M/V/L. У цьому випадку можна здійснити елементарні перетворення для чисельника і знаменника (5.19):
.
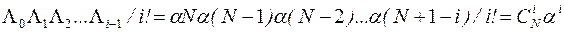Підставивши отриманий вираз у (5.19) отримаємо розподіл Енгсета:
. (5.20)
2. Потік викликів найпростіший із параметром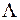 
, дисципліна обслуговування з явними втратами – тобто система M/M/V/L. З (5.19) безпосередньо випливає перший розподіл Ерланга:
Розподіл Ерланга можна одержати також із розподілу Енгсета (5.20), якщо
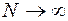, а 
, але так, що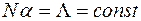 
.
3. Потік викликів примітивний з параметром
,
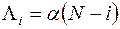дисципліна обслуговування без втрат – система Mi/M/V/LL. Для обслуговування N джерел викликів без втрат необхідно, щоб число виходів у системі
.
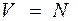При цьому вираз (5.20) з урахуванням бінома Ньютона
приймає вигляд (якщо а = a, b = 1):
. (5.21)
Позначивши
,
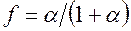після нескладного перетворення маємо розподіл Бернуллі:
(5.22)
4. Потік викликів найпростіший з параметром 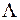, дисципліна обслуговування без втрат – система M/M/V/LL. В цьому випадку число виходів у системі повинно бути необмеженим, тобто 
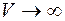. З розподілу (5.21), з урахуванням розкладання функції 
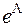в ряд Маклорена 
одержуємо розподіл Пуассона:
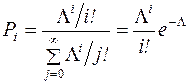. (5.23)
Розподіл Пуассона (5.23) можна також одержати з розподілу Бернуллі (5.22) при 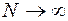та , але так що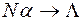 
.
Таким чином, найбільш загальним із розглянутих чотирьох розподілів є розподіл Енгсета. З нього випливає, з одного боку, перший розподіл Ерланга, а з іншого боку - розподіл Бернуллі. З останніх двох, різними засобами, можна одержати розподіл Пуассона.
Необхідно відзначити, що у всіх розглянутих розподілах параметри 
, що характеризують потік викликів, виражені у викл./у.о.ч.(Ерл).
5.5.3 Характеристики якості систем Mі/M/v/L
Імовірність втрат за часом знаходиться з розподілу Енгсета (5.20) як імовірність зайнятості усіх v каналів системи:
(5.24)
Формула (5.24) носить назву формули Енгсета. Значення цієї формули також табульовані у довідковій літературі [1].
Імовірність втрати виклику знаходиться згідно визначенню (3.9):
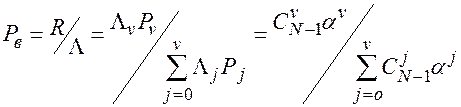(5.25)
Порівняння формул (5.24) і (5.25) показує, що завжди має місце нерівність:
Pt > Pв
Рівність досягається тільки у граничному випадку при N®¥, коли примітивний потік переходить у найпростіший. Вираз (5.25) можна отримати безпосередньо з (5.24), керуючись наступними міркуваннями: виклик, що надійшов від конкретного N-го вільного джерела, буде втраченим, якщо в цей момент зайняті усі v канали. Ця зайнятість забезпечується рештою N-1 джерелом. Тобто
Pв(N, v, a) = Pt(N-1, v, a)
Інтенсивність обслугованого навантаження:
(5.26)
Інтенсивність вхідного навантаження (математичне очікування параметру примітивного потоку викликів):
(5.27)
Інтенсивність потенційного навантаження
, (5.28)
де імовірність Pi визначається за розподілом Бернуллі (5.22). Таким чином, f – інтенсивність потенційного навантаження від одного джерела.
Імовірність втрат за навантаженням знаходимо з урахуванням (5.28) і (5.26):
(5.29)
З (5.29) випливає, що при кінцевому a завжди має місце нерівність:
Pн < Pв
Рівними ці види втрат можуть бути тільки у граничному випадку, коли a®0 і примітивний потік переходить у найпростіший. Враховуючи вищенаведене співвідношення між Pt і Pв, можна записати загальний вираз:
Pн £ Pв £ Pt
Розглянемо різницю:
L – А = aN/[1+a(1-Pв)] – aN/(1+a) = a А Pн
Ця різниця між інтенсивностями потенційного та вхідного навантаження обумовлена наступною особливістю розглянутої моделі. При отриманні відмови у з’єднанні джерело одразу стає вільним і разом з іншими вільними джерелами може надсилати нові виклики. Параметр потоку і, відповідно, інтенсивність вхідного навантаження зростають на величину a А Pн. При цьому добуток АPн визначає інтенсивність втраченого навантаження або середнє число джерел, що стали вільними після отримання відмови, а a є інтенсивність потоку від одного вільного джерела. Якщо припустити, що джерело після отримання відмови блокується на час обслуговування, то збільшення інтенсивності вхідного навантаження не відбудеться і буде мати місце рівність L = А.
Характерно, що в цьому випадку імовірності кількості зайнятих джерел (тих, що обслуговуються і блокуються) розподілені за законом Бернуллі, а розподіл імовірності кількості зайнятих ліній відрізняється від розподілу Енгсета.
Таким чином, при обслуговуванні примітивного потоку взаємодія джерела з системою обслуговування характеризується чотирма типами навантаження, фізичний зміст яких треба чітко розрізняти, оскільки їх чисельні значення неоднакові. Розглянемо ці типи:
1. Інтенсивність потоку викликів від вільного джерела в одну умовну одиницю часу 
, викл/у.о.ч. (Ерл)
2. Середня інтенсивність потоку викликів в одну умовну одиницю часу або інтенсивність навантаження, що надходить від джерела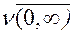 
, викл/у.о.ч. (Ерл). З (5.27):
n = L/N = a/[1+a(1-Pв)] (5.30)
3. Інтенсивність потенційного навантаження від джерела 
, Ерл.
f = a/(1+a) (5.31)
4. Інтенсивність обслугованого навантаження, віднесена до одного джерела 
, Ерл. З (5.26):
y = Y/N = a(1 - Pв)/[1+a(1-Pв)] (5.32)
Порівнюючи (5.30) – (5.32), маємо:
y £ f £ n £ a
Для зручності розрахунків, крім вищенаведених формул можна використовувати також наступні:
•n = a (1-y)
•Y = n (1- Рв) = f(1- Рн)
•a Рн= n Рв
•a = Y/(1-Y)(1- Рв) = n/[1-n (1-Рв)]
•Рн= (1-V/N)Pt= (1-Y) Рв
Отже, якщо при заданих значеннях кількості каналів v та одного з вищенаведених параметрів навантаження відома одна з характеристик якості обслуговування, наприклад Рв, то решту характеристик досить легко визначити.
Приклад 5.7
Розрахувати основні характеристики якості для системи Mі /M/v/L, для якої відома імовірність втрати виклику Рв = 0,03, якщо:
N = 30, v = 6, a = 3 викл/год, h = 120 с
Рішення
Виразимо інтенсивність джерела у вільному стані в ерлангах:
a = a h = 3*120/3600 = 0,1 Ерл
Інтенсивність обслугованого навантаження за (5.26):
Y = 0,1*30*(1-0,03)/[1+0,1*(1-0,03)] = 2,65 Ерл
y = Y/N = 0,0884 Ерл
Інтенсивність потенційного навантаження для одного джерела (5.31):
f = a/(1+a) = 0,1/1,1 = 0,0909 Ерл
A = fN = 2,73 Ерл
Інтенсивність вхідного навантаження за (5.27):
L = 0,1*30//[1+0,1*(1-0,03)] = 2,734 Ерл
Середня інтенсивність джерела(5.30):
n = L/N =2,734/30 = 0,091 Ерл
Таким чином, виконується співвідношення
y £ f £ n £ a
0,0884 < 0,0909 < 0,091 < 0,1