 |
|
Середня тривалість очікування початку обслуговування
Для будь-якого виклику, що надходить в систему, середня тривалість очікування  може розглядатися як відношення сумарної тривалості очікування всіх викликів до кількості викликів, що надійшли в систему. Аналогічно, середня тривалість очікування затриманих в черзі викликів
може розглядатися як відношення сумарної тривалості очікування всіх викликів до кількості викликів, що надійшли в систему. Аналогічно, середня тривалість очікування затриманих в черзі викликів 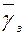 може розглядатися як відношення сумарної тривалості очікування всіх викликів до кількості затриманих викликів. Таким чином,
може розглядатися як відношення сумарної тривалості очікування всіх викликів до кількості затриманих викликів. Таким чином, 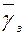 >
>  .
.
Величина  ‑ це інтенсивність потоку затриманих викликів, що створюють чергу середньою довжиною
‑ це інтенсивність потоку затриманих викликів, що створюють чергу середньою довжиною  , де кожний затриманий виклик у середньому очікує
, де кожний затриманий виклик у середньому очікує  . Тоді:
. Тоді:
 (6.10)
(6.10)
З (6.10) і (6.9) можна отримати значення  , виражене в умовних одиницях часу, тобто в одиницях середньої тривалості обслуговування:
, виражене в умовних одиницях часу, тобто в одиницях середньої тривалості обслуговування:
 (6.11)
(6.11)
Враховуючи, що 1 у.о.ч. = h, маємо формулу для обчислення середньої тривалості очікування затриманого виклику в звичайних часових одиницях:

Для оцінки середньої тривалості очікування будь-якого виклику, що надійшов в систему, требі врахувати імовірність очікування. Отже, в умовних та звичайних одиницях часу відповідно:
 (6.12)
(6.12)

Порівнюючи (6.12) і (6.9), отримуємо формулу, відому як формула Літла:
 (6.13)
(6.13)
Ця формула пов’язує середню довжину черги, середній час очікування в умовних одиницях часу та інтенсивність навантаження, що надходить в систему. Подібна формула має місце і для зв’язку середньої довжини черги із середнім часом очікування в звичайних часових одиницях та параметру потоку, що надходить в систему:

6.2.5 Імовірність перевищення довжиною черги заданої величини п
Використовуючи послідовно n+1 разів друге рекурентне співвідношення (6.2), одержуємо:
 (6.14)
(6.14)
Слід зазначити, що всі вищеназвані характеристики не залежать від дисципліни обслуговування черги.
6.2.6 Імовірність очікування більше припустимого часу tпр
Величину  часто називають умовними втратами. На відміну від попередніх характеристик, імовірність
часто називають умовними втратами. На відміну від попередніх характеристик, імовірність  залежить від вигляду черги. Найбільш простий вираз
залежить від вигляду черги. Найбільш простий вираз  утворюється при демократичній черзі (FIFO). Розглянемо цей випадок. Імовірність
утворюється при демократичній черзі (FIFO). Розглянемо цей випадок. Імовірність  можна уявити у вигляді такої суми:
можна уявити у вигляді такої суми:
 , (6.15)
, (6.15)
де  - імовірність очікування понад tпр при надходженні виклику в стані системи i. Очевидно,
- імовірність очікування понад tпр при надходженні виклику в стані системи i. Очевидно,  тільки при
тільки при 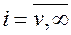 . Для того щоб виклик, що надійшов у стані системи i (довжина чергидорівнює i - v), чекав початку обслуговування більше часу tпр, необхідно, щоб за час tпр, звільнилося не більш ніж (i - v) ліній. Параметр потоку звільнень при наявності черги постійний і дорівнює v. У цьому випадку потік звільнень є найпростішим і імовірність звільнення k ліній за час tпр є
. Для того щоб виклик, що надійшов у стані системи i (довжина чергидорівнює i - v), чекав початку обслуговування більше часу tпр, необхідно, щоб за час tпр, звільнилося не більш ніж (i - v) ліній. Параметр потоку звільнень при наявності черги постійний і дорівнює v. У цьому випадку потік звільнень є найпростішим і імовірність звільнення k ліній за час tпр є
 (6.16)
(6.16)
Тоді
 . (6.17)
. (6.17)
Підставивши (6.16) і (6.17) у (6.15), після ряду перетворень одержуємо:
 . (6.18)
. (6.18)
Величина tпр у (6.18) виражена в умовних одиницях часу.