Главная | Обратная связь

Другий розподіл Ерланга

Розглянута нижче модель багато в чому аналогічна першій задачі Ерланга. v-канальна СМО обслуговує найпростіший потік викликів. Час обслуговування одного виклику – випадкова величина з експоненціальним розподілом та середнім значенням, прийнятим за одиницю часу (h=1у.о.ч.). Тоді параметр потоку виклику 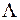, виражений у викликах за у.о.ч. (тобто, ерлангах), можна розглядати як інтенсивність вхідного навантаження. При зайнятості всіх v каналів виклик, що надійшов, стає в чергу й обслуговується після деякого очікування. Загальне число викликів, що знаходяться в системі на обслуговуванні та в черзі, позначимо 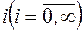та назвемо станом системи. При 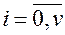величина i характеризує число зайнятих виходів у системі, при 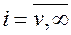число зайнятих виходів дорівнює v, а різниця (і – v) є довжина черги. Параметр потоку звільнень визначається числом зайнятих виходів і в першому випадку, при 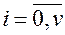,залежить від стану системи i(тобто є примітивним), а в другому, при 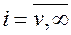, має постійне значення v, (тобто є найпростішим):

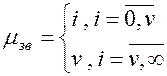
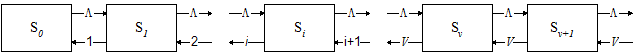
Рисунок 6.1. Граф станів СМО з очікуванням

Імовірність того, що система в усталеному режимі знаходиться в стані iпозначимо через P_i. Залежно від номеру стану та відповідного типу потоку звільнень (найпростішого або примітивного) система рівнянь для стану статистичної рівноваги (усталеного режиму) має такий вид:

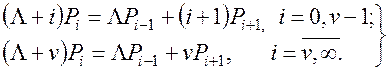(6.1)

Позначимо для і при 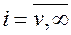. Тоді з (6.1) одержуємо , звідки випливають два рекурентних співвідношення для обчислення імовірностей P_i:

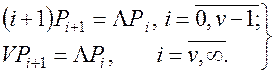(6.2)

Приймаючи значення i послідовно рівними 0, 1, 2,... , одержуємо:

i = 0 P₁ =L/1* P₀ ,

i = 1 P₂ =L/2* P₁ = L²/2!* P₀

…

i = v-1 P_v =L/2* P_v-1 = L^v/v!* P₀

i = v P_v+1 =L/v* P_v =L/v*L^v/v!* P₀ =

i = v+1 P_v+2 =L/v* P_v+1 = 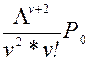= (L/v)^i-v*(L^v/v!)* P₀

Таким чином,

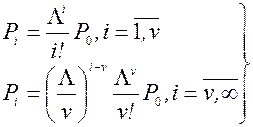(6.3)

 

Для визначення імовірності Р₀ скористаємося умовою нормування з урахуванням (6.3)

Р₀ + L/1* P₀ + L²/2!* P₀ + …+ L^v/v!* P₀ + L/v*L^v/v!* P₀ + ...+(L/v)^i-v*(L^v/v!)* P₀ =

= Р₀[ ] = 1

Звідки

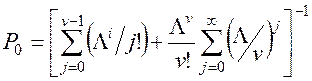. (6.4)

 

Вираз 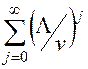в (6.4) є сума нескінченної геометричної прогресії. При ряд 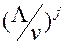розходиться. Відповідно 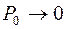, і всі імовірності 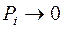при кінцевому значенні i. Можна показати, що 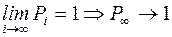. Це означає, що при інтенсивності навантаження L, яка дорівнює або перевищує число виходів системи v, з імовірністю 1 постійно будуть зайняті усі виходи, а довжина черги буде нескінченною. Тому, щоб система могла функціонувати нормально, а черга не зростала нескінченно, необхідно виконати умову 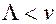. У цьому випадку прогресія буде убувати, а сума її 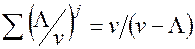. Відповідно

 

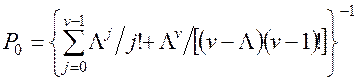(6.5)

 

З урахуванням (6.3) і (6.5) одержуємо другий розподіл Ерланга:

 

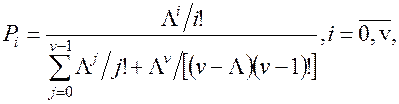
(6.6)

Слід запам’ятати: цей вираз можна використовувати тільки при дотриманні умови існування усталеного режиму: L < v .

Приклад 6.1.

Для системи М/М/2/W, на вхід якої надходить навантаження з інтенсивністю 1 Ерл. обчислити:

1) частку часу, який система простоює

2) імовірність зайнятості 1 каналу в системі

3) імовірність знаходження у черзі 1 виклику.

Побудувати граф станів системи

Рішення

Маємо двоканальну систему з очікуванням, на вхід якої надходить найпростіший потік викликів, час обслуговування розподілено за експоненційним законом. Граф станів представлено на рисунку:

1) Оскільки граничні імовірності характеризують частку часу, яку система знаходиться у відповідному стані, то для обчислення частки часу, який система простоює, треба знайти P₀ за першою частиною (6.6):

P₀ = 1/(1+1+1) = 1/3

2) Імовірність зайнятості 1 каналу в системі – це P_{1 .} Використовуючи те, що в усіх виразах (6.6) знаменник однаковий:

P₁ = 1/3

3) Імовірність знаходження у черзі 1 виклику – це P_3, обчислюється за другою частиною (6.6):

P₃ = [1/2!*(1/2)^3-2]/3 = 1/12