Главная | Обратная связь

Равновесие плоской системы сил. Случай параллельных сил

Необходимые и достаточные условия равновесия любой системы сил даются равенствами

, ,

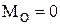выражаемыми формулами (24). Найдем вытекающие отсюда аналитические условия равновесия плоской системы сил.

1. Основная форма условий равновесия. Так как вектор равен нулю, когда равны нулю его проекции R_x и R_y, то для равновесия должны выполняться равенства R_x = 0, R_y = 0 и M_O = 0, где в данном случае M_O – алгебраический момент, а О – любая точка в плоскости сил. Но из формул (26) следует, что предыдущие равенства будут выполнены, когда действующие силы удовлетворяют условиям:

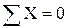, , . (28)

Формулы (28) выражают следующие аналитические условия равновесия: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю. Одновременно равенства (28) выражают условия равновесия твердого тела, находящегося под действием плоской системы сил.

2. Вторая форма условий равновесия: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов сил относительно каких-нибудь двух центров А и В и сумма их проекций на ось Оx, не перпендикулярную прямой АВ, были равны нулю:

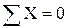, , . (29)

Необходимость условий очевидна, так как если любое из них не выполняется, то 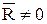или ; или ( ) и равновесия не будет. Докажем их достаточность. Если для данной системы сил выполняются только первые два из условий (35), то для нее M_A = 0 и M_B = 0. Такая система может не находится в равновесии, а иметь равнодействующую , одновременно проходящую через точки А и В (рис. 26). Но по третьему условию должно быть . Так как ось Оx проведена не перпендикулярно к АВ, то последнее условие может быть выполнено, только когда , т.е. когда имеет место равновесие.

Рис. 26

3. Третья форма условий равновесия (уравнения трех моментов): для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно любых трех центров А, В и С, не лежащих на одной прямой, были равны нулю:

, , . (30)

Необходимость условий очевидна. Достаточность условий (30) следует из того, что если при одновременном выполнении этих условий данная система сил не находилась бы в равновесии, то она должна была бы приводится к равнодействующей, одновременно проходящей через точки А, В и С, что невозможно, так как эти точки не лежат на одной прямой. Следовательно, при выполнении условий (30) имеет место равновесие.

4. Равновесие плоской системы параллельных сил. В случае, когда силы параллельны друг другу, можно направить ось Оx перпендикулярно силам, а ось Оy параллельно им (рис. 27). Тогда проекция каждой из сил на ось Оx будет равна нулю и первое из равенств (28) обратится в тождество вида . В результате для параллельных сил останется два условия равновесия:

, . (31)

где Оy параллельна силам.

Другая форма условий равновесия для параллельных сил, получающаяся из равенств (29), имеет вид:

, . (32)

При этом точки А и В не должны лежать на прямой, параллельной силам.

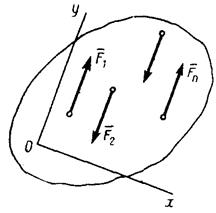
Рис. 27

Решение задач

Решение многих задач статики сводится к определению реакций опор, с помощью которых закрепляются балки и мостовые фермы.

В технике обычно встречаются три типа опорных закреплений (кроме рассмотренных в § 2):

1. Подвижная шарнирная опора (рис. 28, опора А). Реакция такой опоры направлена по нормали к поверхности на которую опираются катки подвижной опоры.

2. Неподвижная шарнирная опора (рис. 28, опора В). Реакция такой опоры проходит через ось шарнира и может иметь любое направление в плоскости чертежа. При решении задач будем реакцию изображать ее составляющими и по направлениям координатных осей. Модуль определим по формуле .

3. Жесткая заделка (рис. 29, а). Рассматривая заделанный конец балки и стену как одно целое, жесткую заделку изображают так, как показано на рис. 29, б. В этом случае на балку в ее поперечном сечении действует со стороны заделанного конца система распределенных сил (реакций). Считая эти силы приведенными к центру А сечения, можно их заменить одной силой и парой с неизвестным моментом m_A (рис. 29, а). Силу можно изобразить ее составляющими 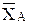, (рис. 29, б).

Таким образом, для нахождения реакции жесткой заделки надо определить три неизвестные величины X_A, Y_A, m_A.

Рис. 28 Рис. 29

Отметим также, что в инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль поверхности по тому или иному закону. Рассмотрим некоторые примеры распределенных сил.

Плоская система распределенных сил характеризуется ее интенсивностью q, т.е. значением силы, приходящейся на единицу длины нагруженного отрезка. Измеряется интенсивность в ньютонах, деленных на метры (Н/м).

а) Силы, равномерно распределенные вдоль отрезка прямой (рис. 30, а). Для такой системы интенсивность q имеет постоянное значение. При расчетах эту систему сил можно заменить равнодействующей 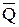. По модулю

Q = aq . (33)

Приложена сила Q в середине отрезка АВ.

б) Силы, распределенные вдоль отрезка прямой по линейному закону (рис. 30, б). Для этих сил интенсивность q является величиной переменной, растущей от нуля до максимального значения q_m. Модуль равнодействующей 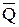в этом случае определяется по формуле

Q = 0,5aq_m . (34)

Приложена сила 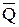на расстоянии а/3 от стороны ВС треугольника АВС.

 

 

Рис. 30

 

Задача 3. Определить реакции неподвижной шарнирной опоры А и подвижной опоры В балки (рис. 31), на которую действуют активные силы: одна известная сосредоточенная сила F = 5 кН, приложенная в точке С под углом 60⁰, и одна пара сил с моментом m = 8 кНм.

 

Рис. 31

 

Решение. 1) Выбираем объект исследования, т.е. рассматриваем равновесие балки АВС. 2) Изобразим внешние силы, действующие на балку: силу , пару сил с моментом m и реакции связей 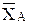, , (реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими). В результате имеем произвольную плоскую систему сил. 3) Проведем координатные оси x, y и составляем условия равновесия (28). Для вычисления момента силы , иногда, удобно разложить ее на составляющие и 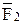, модули которых равняются F₁ = F cos60⁰ = 2,5 кН, F₂ = F cos30⁰ = 4,33 кН. Тогда получим:

, ,

.

Решая эту систему уравнений, найдем:

X_A = F₁ = 2,5 кН, Y_B = (m + F₂∙5)/3 = 9,88 кН, Y_A = F₂ – Y_B = – 5,55 кН.

Знак минус реакции Y_A показывает, что эта реакция направлена вертикально вниз.

Для проверки составим уравнение моментов относительно нового центра, например, относительно точки В:

, 5,55∙3 – 8 – 4,33∙2 = – 0,01 ≈ 0.

Задача 4. Определить реакции заделки консольной балки (рис. 32), на которую действуют активные силы: сосредоточенная сила F = 6 кН, приложенная в точке С под углом 45⁰, равномерно распределенная нагрузка интенсивностью q = 2 кН/м и пара сил с моментом m = 3 кНм.

 

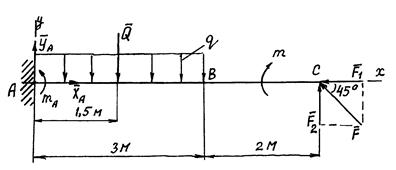
Рис. 32

 

Решение. 1) Выбираем объект исследования, т.е. рассматриваем равновесие балки АВС. 2) Изобразим внешние силы, действующие на балку: силу , равномерно распределенную нагрузку интенсивностью q, пару сил с моментом m и реакции заделки, т.е. три неизвестные величины X_A, Y_A, m_A (реакцию жесткой заделки изображаем двумя ее составляющими X_A, Y_A, а пару – неизвестным моментом m_A, как на рис. 29). Силу разложим на две составляющие и , модули которых равняются F₁ = F₂ = F cos45⁰ = 4,24 кН, а распределенную нагрузку интенсивностью q заменим сосредоточенной силой с модулем равным

Q = 3∙q = 6 кН.

Сила 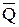приложена в середине отрезка АВ. В результате имеем произвольную плоскую систему сил. 3) Проведем координатные оси x, y и составляем уравнения равновесия (2):

 

, ,

.

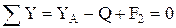Решая эти уравнения, найдем:

X_A = F₁ = 4,24 кН, Y_A = Q – F₂ = 1,76 кН, m_A = Q∙1,5 + m – F₂∙5 = – 9,2 кНм.

Для проверки составим уравнение моментов относительно точки С:

, – 9,2 + 21 – 3 – 8,8 = 0.

Задача 5. Определить реакции опор А, В, С и усилие в промежуточном шарнире D составной конструкции (рис. 33), на которую действуют активные силы: сосредоточенная сила F = 4 кН, приложенная в точке Е под углом 45⁰, равномерно распределенная нагрузка интенсивностью q = 2 кН/м и пара сил с моментом m = 10 кНм.

 

 

Рис. 33

 

Решение. Один из способов решения задач об определении реакции опор составной конструкции состоит в том, что конструкцию расчленяют на отдельные тела и составляют условия равновесия каждого из тел в отдельности. Воспользуемся этим способом и разобьем конструкцию на две части: левую AD и правую DC. В результате приходим к задаче о равновесии двух тел. Силовые схемы задачи показаны на рис. 7,8. Для упрощения вычислений разложим силу на составляющие и 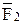, модули которых равны F₁ = F₂ = F cos45⁰ = 2,83 кН, а распределенную нагрузку интенсивностью q заменим сосредоточенной силой 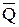с модулем равным Q = 10 кН. Сила 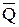приложена в середине отрезка BD.

 

Рис. 34 Рис. 35

Анализ приведенных силовых схем показывает, что они включают шесть неизвестных величин: X_A, Y_A, Y_B, X_D, Y_D, Y_C.

Так как на рис. 34,35 имеются плоские системы уравновешенных сил, то для них можно записать условия равновесия (28) в виде шести линейных алгебраических уравнений:

Левая часть Правая часть

, ,

, ,

, .

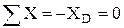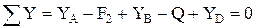Поскольку составленная система шести уравнений зависит от шести неизвестных X_A, Y_A, Y_B, X_D, Y_D, Y_C, то она является замкнутой.

Решая систему, найдем:

X_A = – 2,83 кН, Y_A = – 0,93 кН, Y_B = 11,76 кН, Y_C = 2 кН, X_D = 0, Y_D = 2 кН.

Для проверки составим уравнение моментов относительно точки D:

= 2,83∙7 – (– 0,93)∙15 – 11,76∙5 + 10∙2,5 – 10 + 2∙5 = – 0,04 ≈ 0.