Главная | Обратная связь

ЛЕКЦИЯ 10. СОВРЕМЕННАЯ СТОИМОСТЬ ПОСТОЯННОЙ РЕНТЫ ПОСТНУМЕРАНДО

Годовая рента. Вместо термина "современная стоимость" (современная вели­чина) потока платежей в зависимости от контекста употребля­ют также термины капитализированная стоимость или приведенная ве­личина. Как было показано выше, современная стоимость пото­ки платежей эквивалентна в финансовом смысле всем плате­жам, которые охватывает поток. Методы расчета современных стоимостей финансовых рент обсудим в том же порядке, что и методы наращения рент и почти столь же детально. Начнем с самого простого случая – годовой ренты постнумерандо, член которой равен R, срок ренты п, ежегодное дисконтирование. Рента немедленная. В этих условиях дисконтированная величина первого платежа равна Rv, второго –Rv², последнего –Rvⁿ. Как видим, эти величи­ны образуют ряд, соответствующий геометрической прогрессии с первым членом Rv и знаменателем v. Обозначим сумму чле­нов этой прогрессии через А:

(1)

Назовем множитель, на который умножается R, коэффициен­том приведения ренты, он обозначен как a_n;i. Этот коэффициент характеризует современную стоимость ренты с членом, равным 1.

Поскольку рассматриваемый параметр часто применяется в финансовых расчетах, полезно обратить внимание на некоторые его свойства. Очевидно, что чем выше значение i, тем меньше величина коэффициента. Нетрудно показать, что при i = 0 a_n;i=n.

При увеличении срока ренты величина a_n;i стремится к не­которому пределу. При п =¥ предельное значение коэффици­ента составит

a_¥;i =1/i. (2)

Полученное выражение применяется при расчете современ­ной стоимости вечной ренты, о чем пойдет речь в 4.5. График зависимости a_n;i от п показан на рис. 4.2.

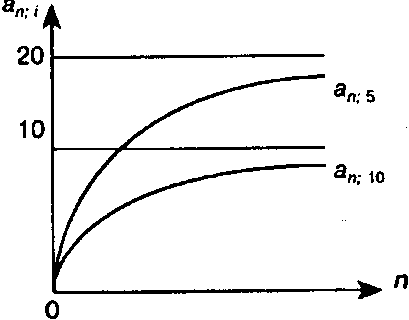Рис.4.2

ПРИМЕР 10.1. Годовая рента постнумерандо характеризуется па­раметрами: R= 4 млн. тг., n= 5. При дисконтировании по слож­ной ставке процента, равной 18,5 % годовых, получим

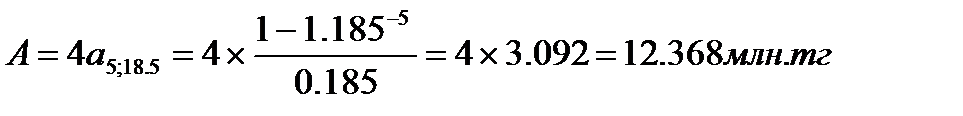
Таким образом, все будущие платежи оцениваются в настоя­щий момент в сумме 12,368 млн. тг. Иначе говоря, 12,368 млн. тг., размещенных под 18,5% годовых, обеспечивают ежегодную выплату по 4 млн. тг. в течение 5 лет.

Заметим, что формула (1) может быть применена и для определения современной стоимости р-срочной ренты. В этом случае переменная п означает число периодов ренты, а i– став­ку за один период (но не годовую).

Рента p-срочная(р =т). Число членов ренты здесь равно числу начислений процентов; величина члена ренты составляет R/m . В итоге

(5)

Этот же результат можно получить и по формуле (1) и при этом воспользоваться таблицей коэффициентов приведения по­стоянных рент. В этом случае вместо числа лет берется количе­ство периодов ренты, процентная ставка и величина члена рен­ты определяются соответствующим образом.

Рента р-срочная (р¹ т). Сумма членов соответствующей прогрессии составит

(6)

Ренты с непрерывным начислением процентов. Пусть, как и выше, ряд состоит из ежегодных платежей, равных R, однако проценты начисляются непрерывно, сила роста равна d. При дисконтировании по этой ставке всех членов ряда получим геометрическую прогрессию с первым членом R и знаменате­лем e^-d. Сумма членов прогрессии находится по формуле:

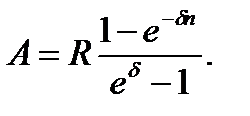(7)

Если имеет место р-срочная рента с непрерывным начисле­нием процентов, то

(8)