Главная | Обратная связь

Ренты пренумерандо и ренты с выплатами в середине периодов.

Напомним, что под рентой пренумерандо понимается рента с платежами в начале периодов. Легко понять, что каждый член такой ренты "работает" на один период больше, чем в ренте по­стнумерандо. Отсюда наращенная сумма ренты пренумерандо, обозначим ее здесь как , больше в (1 + i) раз аналогичной ренты постнумерандо: = S(1 +i).

Аналогичным путем получим для годовой ренты с начисле­нием процентов т раз в году = S(1 + j/m)^т.

Для р-срочных рент, у которых т = 1 и т¹р, получим:

= S(1 + i)^1/р, 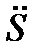= S(1 + j/m)^{т /р}.

Точно такая же зависимость наблюдается и между современ­ными стоимостями и коэффициентами приведения рент постнумерандо и пренумерандо:

= A(1 + i); и т.д.

Важной для практики является рента с платежами в середи­не периодов. Например, в случаях, когда поступления от произ­водственных инвестиций распределяются более или менее рав­номерно, применение рент пренумерандо или постнумерандо для описания таких потоков может привести к некоторым сме­щениям в значении получаемых показателей. В таких ситуациях для уменьшения погрешности рекомендуется суммы поступле­ний за период относить к середине периодов. Наращенные сум­мы и современные стоимости таких рент находим умножением соответствующих обобщающих характеристик рент постнуме­рандо на множитель наращения за половину периода. Так, для современных стоимостей находим следующие соотношения:

А_1/2 = A(1+i)^1/2 при р = 1, т = 1,

А_1/2= А(1+i)^1/2p при р> 1, т = 1,

А_1/2= А(1 +j/m)^m/² при р = 1, т > 1,

А_1/2 = A(1 + j/m)^m/^2p при р> 1, т > 1.

ПРИМЕР 11.1. Определим поправочный множитель, необходи­мый для расчета современной стоимости ренты с платежами в середине периодов. Условия ренты постнумерандо: р = 12, m = 1, i = 10%. Искомый множитель l.l^1/(2´12) = 1,00398.

Вечная рента. Напомним, что под вечной рентой (perpetuity) понимается ряд платежей, количество которых не ограничено – теоретически она выплачивается в течение бесконечного числа лет. В практике иногда сталкиваются со случаями, когда есть смысл прибегнуть к такой абстракции, например, когда предполагается, что срок потока платежей очень большой и конкретно не оговаривается. Очевидно, что наращенная сумма вечной ренты равна беско­нечно большой величине. Современная величина вечной ренты есть конечная величина, которая определяется весьма просто. Ранее было показано (что при п®¥ пределом для коэффициента приведения является a_¥;i =1/i. От­куда для вечной ренты находим

А_¥ =R/i. (2)

Таким образом, современная стоимость вечной ренты зависит только от размера члена ренты и процентной ставки. Из (4.24) следует

R= А_¥i, (3)

т.e. член вечной ренты равен проценту от ее капитализирован­ной стоимости.

Нетрудно убедиться в том, что отдаленные платежи оказыва­ют весьма малое влияние на величину коэффициента приведе­ния. С ростом п прирост этого показателя уменьшается (см. рис. 4.2). В силу сказанного при больших сроках ренты и высо­ком уровне ставки для определения современной стоимости можно воспользоваться формулой (4.24) без заметной потери точности. Например, для ограниченной ренты при i = 20%, n = 100 и R = 1 получим точное значение: А = 4,999999, а по формуле (4.24) находимА_¥= 5.

Для других видов рент получим:

при р>1, т=1;

при р=т>1.

Рента с периодом платежей, превышающим год. В анализе производственных инвестиционных проектов иногда встреча­ются с рентами, члены которых выплачиваются с интервалами, превышающими год. Определим наращенную сумму и совре­менную стоимость таких рент.

Пусть r– временной интервал между двумя членами ренты, проценты начисляются раз в году. В этом случае современная стоимость ренты равна:

(4)

гдеТ– величи­на члена ренты, п–срок ренты, кратный r.

Разумеется, указанное в формуле соотношение коэффициен­тов приведения и наращения можно использовать в случаях, когдаr– целое число лет.

Переменная процентная ставка. На практике иногда сталки­ваются с потоками платежей, предполагающих применение пе­ременных во времени процентных ставок, например, при рест­руктурировании задолженности. Так, в последнем случае для облегчения положения должника применяются низкие ставки в первые годы выплат процентных платежей и более высокие в последующие.