 |
|
Диференціальні рівняння, що допускають відокремлювання змінних.
Диференціальне рівняння першого порядку називається рівнянням з відокремлюваними змінними, якщо його можна подати у вигляді:
. (9.1)
Права частина рівняння (9.1) являє собою добуток двох множників, кожний з яких є функцією тільки одного аргументу.
Наприклад, рівняння 
є рівняння з відокремлюваними змінними, оскільки в ньому можна прийняти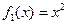 
і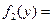 
. Так саме, рівняння 
є рівняння з відокремлюваними змінними, оскільки його можна записати у вигляді (9.1): 
, де 
, 
.
Напроти, рівняння 
неможна подати у вигляді (9.1), і, отже, воно не є рівнянням з відокремлюваними змінними.
Метод інтегрування рівняння з відокремлюваними змінними полягає ось в чому.
Перепишемо рівняння (9.1) у вигляді 
. Тоді:
. (9.2)
Якщо рівняння (9.1) подано у вигляді (9.2), то кажуть, що в ньому відокремлені змінні.
Припустимо, що ми знайшли розв’язок 
рівняння (9.2). Якщо цю функцію підставимо в рівняння (9.2), то воно перетвориться на тотожність; інтегруючи його почленно, отримаємо
,
або
, (9.3)
де 
- довільна стала.
Вираз (9.3) являє собою загальний інтеграл рівняння (9.2).
Зауваження. Розділивши обидві частини рівняння (9.1) на 
, ми можемо втратити ті розв’язки, за яких 
. Дійсно, якщо при 
, то функція-константа , очевидно, є розв’язком рівняння (9.1).
Приклад 9.1. Розв’язати рівняння 
.
Розв’язання. Розв’язуючи рівняння відносно 
, отримаємо 
, або 
. Бачимо, що змінні відокремлені. Інтегруючи, отримуємо 
, де 
- довільна стала. Для спрощення отриманого розв’язку скористуємось часто застосовним засобом; покладемо (зазначимо, що при зміні 
від 0 до 
величина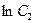 
змінюється від 
до 
) 
( 
), тоді 
, звідки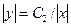 
, або 
. Покладаючи 
, остаточно отримаємо
,
де 
- довільна стала. Геометрично отриманий загальний розв’язок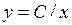 
являє собою родину рівнобічних гіпербол.
Нехай треба з отриманого загального розв’язку виділити частинний розв’язок, який задовольняє початкову умову 
. Замінюючи в рівності 
та 
початковими даними, отримаємо співвідношення 
, з якого знайдемо 
. Таким чином, шуканий частинний розв’язок має вигляд 
.
9.2.2. Однорідні відносно незалежної змінної та шуканої функції диференціальні рівняння.
Звичайне диференціальне рівняння першого порядку 
називається однорідним відносно незалежної змінної та шуканої функції, якщо функція 
є однорідною відносно х та у.
Функція 
є однорідною n-го виміру відносно х та у, якщо 
, диференціальне рівняння 
є однорідним відносно х та у, якщо є однорідною функцією нульового виміру, а це означає, що функція може бути подана як функція однієї змінної, тобто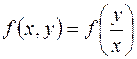 
.
Спосіб розв’язку однорідного звичайного диференціального рівняння першого порядку полягає в тому, що заміна змінної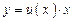 
, а тоді 
, приводить однорідне диференціальне рівняння до виду рівняння, яке допускає відокремлення змінних.
Задача 9.2. Знайти загальний інтеграл рівняння:
.
Розв’язання. Переконаємось в тому, що дане рівняння є однорідним:
Тоді:
.
та
;
.
Після відокремлювання змінних, маємо, що
.