 |
|
Применение рядов к приближенным вычислениям.
Вычисление значений функций.
Задача.Значение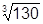 
вычислить с точностью до 0,001.
Решение:. 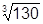приведем к виду 
, где 
.
. 
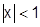, поэтому верно биномиальное разложение: 
начиная со 2-го члена это ряд Лейбницевского типа, можно проверить монотонное стремление к 0 модуля n-го члена: поэтому 
– уже 4-й член меньше 0,0001 , поэтому 
, поэтому возьмем в качестве приближенного значения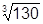 
:
.
Вычисление интегралов.
Если интеграл не берется в конечном виде в элементарных функциях, или получается очень сложная функция, то можно его вычислить, используя его разложение в степенной ряд.
Задача. Вычислить интеграл 
с точностью до 
.
Решение: Это не "берущийся" интеграл.
– это не знакочередующийся ряд, поэтому нельзя остаток оценивать 
-м членом.
Оценим его иначе:
Увеличим все члены, начиная со второго, с тем, чтобы получить геометрический ряд: 
=
= 
.
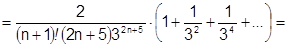
Подберем n таким, чтобы
.
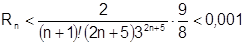Годится n=1, поэтому:
.
Вопросы для самоконтроля по главе 2.
1. Когда говорят, что функциональная последовательность (ряд) сходится на некотором множестве?
2. Что представляет собой сумма функционального ряда?
3. Что общего и чем отличается использование признаков Даламбера и Коши (радикального) при исследовании абсолютной сходимости числового ряда и при отыскании области сходимости функционального ряда?
4. Может ли предельная функция функциональной последовательности, все члены которой непрерывны, оказаться разрывной функцией?
5. Может ли сумма ряда, все члены которого непрерывны оказаться разрывной функцией?
6. Первый член сходящегося ряда – разрывная функция, все остальные члены – непрерывные функция. Можно ли утверждать, что сумма ряда есть разрывная функция?
7. Функциональный ряд равномерно сходится на отрезке. Сходится ли он на этом отрезке?
8. Для некоторого сходящегося на отрезке функционального ярда признак Вейерштрасса равномерной сходимости не выполняется. Можно ли утверждать, что ряд на этом отрезке сходится неравномерно?
9. Члены ряда – непрерывные функции, сумма – разрывная функция. Что можно сказать о характере сходимости ряда?
10. Члены ряда и сумма ряда непрерывны на этом отрезке. Можно ли утверждать, что ряд сходится на этом отрезке?
11. Что означает фраза "функциональный ряд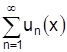 
можно почленно интегрировать на 
"?
12. Что означает фраза "функциональный ряд 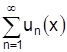можно почленно дифференцировать в точке 
"?
13. Ряд с дифференцируемыми членами сходится равномерно. Можно ли утверждать, что этот ряд можно почленно дифференцировать?
14. Производные членов функционального ряда существуют и непрерывны. Ряд, составленный из производных, сходится равномерно на . Можно ли исходный ряд почленно дифференцировать?
15. Для некоторого функционального ряда выполнено условие теоремы о почленном дифференцировании. Что можно сказать о характере его сходимости?
16. Может ли область сходимости степенного ряда в действительной области состоять из двух непересекающихся промежутков?
17. Чем отличаются области сходимости рядов 
и 
? В каком случае области сходимости этих рядов совпадают?
18. Какие признаки можно использовать для отыскания области сходимости степенного ряда? В каких случаях применяется тот или иной признак?
19. Какие утверждения использовались при доказательстве равномерной сходимости степенного ряда в круге 
?
20. Может ли сумма степенного ряда в круге его сходимости оказаться разрывной?
21. Чем могут отличаться области сходимости двух степенных рядов, один из которых составлен из производных от членов другого?
22. В каком случае заведомо совпадают области сходимости степенного ряда и ряда, составленного из производных от его членов?
23. Сформулируйте теорему о почленном интегрировании степенного ряда. Какие факты используются при ее доказательстве?
24. Сформулируйте теорему о почленном дифференцировании степенного ряда. Какой материал используется при ее доказательстве?
25. Если бы в задаче ряд окажется рядом лейбницевского типа, то как можно выбрать числа членов ряда, которые нужно сохранить для получения ответа с заданной точностью?