 |
|
Определить сходимость ряда по определению сходимости
Числовые ряды
Понятие числового ряда
Рассмотрим бесконечную числовую последовательность действительных чисел:
U1 , U2 , …,Un ,….
где  - функция целочисленного аргумента n.
- функция целочисленного аргумента n.
Последовательность считается заданной, если задан закон, по которому можно найти ее член.
Например:

1,4,9,…,n2,…
Выражение
 (1)
(1)
называется бесконечным числовым рядом, т.е. ряд – это сумма бесконечного числа слагаемых U1, U2, …,Un,….
Числа U1, U2, …,Un,…называются членами ряда, а  - общим членом данного ряда (1).
- общим членом данного ряда (1).
Числа: 


. . . . . . . . . . . . . . .
Sn = U1 + U2 +U3 + …+ Un;
называются частичной суммой ряда (1)
Сумма n первых членов ряда (1)

| |

называется остатком ряда(1).
Ряд (1) называется сходящимся, если его n – я частичная сумма Sn при неограниченном возрастании n стремится к конечному пределу, т.е.
 (2)
(2)
где S – сумма ряда. В этом случае записывают

Если же при  предел частичной суммы Sn не существует или же он бесконечен, то ряд называется расходящимся и суммы не имеет.
предел частичной суммы Sn не существует или же он бесконечен, то ряд называется расходящимся и суммы не имеет.
Пример 1. Найти сумму ряда.

Представим общий член ряда  в виде суммы элементарных дробей, для этого воспользуемся методом неопределенных коэффициентов.
в виде суммы элементарных дробей, для этого воспользуемся методом неопределенных коэффициентов.




таким образом, А=1, В= -1
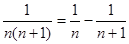
| |
| |
7. Определить область сходимости функционального ряда.
а) 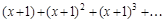
б) 
в) 
8. а) Разложить  в ряд Тейлора по степеням разности
в ряд Тейлора по степеням разности  ,пользуясь определением ряда Тейлора;
,пользуясь определением ряда Тейлора;
б) Разложить  в ряд Маклорена, пользуясь стандартными разложениями.
в ряд Маклорена, пользуясь стандартными разложениями.
а) 
б) 
9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).
а) 

10. а)Найти неопределённый интеграл;
б) Найти или вычислить, определённый интеграл;
в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).
а) 
б) 
в) 
11. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 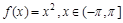
б) 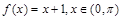 по синусам.
по синусам.
12. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б)  по косинусам.
по косинусам.
Вариант№31
1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.
а) 
б) 
2. Исследовать ряды на сходимость по определению сходимости.
а) 
б) 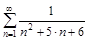

3. Исследовать ряды на сходимость с помощью признака сравнения.
а) 
б) 
4. То же с помощью признака Даламбера.
а) 
б) 
5. То же с помощью интегрального (Коши-Маклорена) признака.
а) 
б) 
6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.
а) 
б) 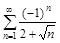

Следовательно

Таким образом, данный ряд является сходящимся и его сумма равна 1, т.е.

Пример 2.
Определить сходимость ряда по определению сходимости
1+1+…+1+…
Найти сумму ряда:

тогда

т.о. данный ряд является расходящимся.
Пример 3.
Определить сходимость ряда
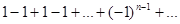
Если последовательность имеет предел, то любая ее под последовательность имеет тот же предел.
Найдем

Следовательно, 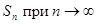 не стремится ни к какому пределу; данный ряд расходится.
не стремится ни к какому пределу; данный ряд расходится.
Пример 4.
| |
| |

Запишем общий член ряда  в виде:
в виде:

Найдем сумму ряда:

где 


. . . . . . . . . .

тогда 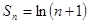
Отсюда 
Ряд расходится.
Пример 5.
Найти сумму ряда 
Заметим, что 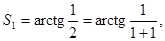
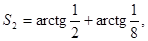

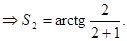
| |
 Как и раньше находим
Как и раньше находим
| |
7. Определить область сходимости функционального ряда.
а) 
б) 
в) 
8. а) Разложить  в ряд Тейлора по степеням разности
в ряд Тейлора по степеням разности  ,пользуясь определением ряда Тейлора;
,пользуясь определением ряда Тейлора;
б) Разложить  в ряд Маклорена, пользуясь стандартными разложениями.
в ряд Маклорена, пользуясь стандартными разложениями.
а) 
б) 
9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).
а) 

10. а)Найти неопределённый интеграл;
б) Найти или вычислить, определённый интеграл;
в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).
а) 
б) 
в) 
11. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б)  по косинусам.
по косинусам.
12. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б)  по синусам.
по синусам.
Вариант№30
1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.
а) 
б) 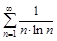
2. Исследовать ряды на сходимость по определению сходимости.
а) 
б) 


3. Исследовать ряды на сходимость с помощью признака сравнения.
а) 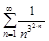
б) 
4. То же с помощью признака Даламбера.
а) 
б) 
5. То же с помощью интегрального (Коши-Маклорена) признака.
а) 
б) 
6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.
а) 
б) 

Откуда,  и
и
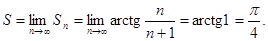
Геометрический ряд
Ряд
a + aq +aq2 + aq3 + …+ aqn+… (*)
называется геометрическим, если его члены представляют собой члены геометрической прогрессии, первый член которой равен а, а знаменатель прогрессии – q.
Рассмотрим п –ую частичную сумму этого ряда
Sn = a + aq + aq2 + aq3 +…+ aqn+…
Она равна сумме членов геометрической прогрессии (если
q  1), т.е.
1), т.е.
 .
.
Найдём предел последовательности частичных сумм геометрического ряда.
1) Если  < 1, то
< 1, то  , поэтому
, поэтому
 .
.
2)
| |
| |
 > 1, то
> 1, то  не существует, а значит и последовательность частичных сумм не имеет предела.
не существует, а значит и последовательность частичных сумм не имеет предела.
3) Если q = 1,то имеем ряд а + а + а + …+ а +…Его п-я частичная сумма Sn = na . При  , в зависимости от знака а.
, в зависимости от знака а.
4) Если q = -1, то имеем ряд а – а + а – а + …+(-1)п-1а+… Его частичные суммы попеременно равны а и о: S1 = a, S2 = 0, S3 = a,…, Sn = 0, т.е. 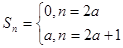 ,
,
но такая последовательность предела не имеет.
Итак, геометрический ряд (*) сходится, если  <1 и его сумма
<1 и его сумма  , а расходится если
, а расходится если 
 1.
1.