 |
|
Интегральный признак Коши.
Если ряд 
(1) таков, что, начиная с некоторого m выполняется неравенство: 
и существует не возрастающая при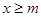 
непрерывная функция 
что 
. . . . . . . . . . .
| |
…
| |
то, 1) ряд (1) сходится, если сходится 
;
2) ряд (1) расходится, если расходится .
Доказательство:
Общность рассуждений не нарушится, если принять m=1. Тогда при х=1, 2, 3, … найдем соответствующие ординаты
. . . . . . .
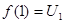
построим точки, соединим кривой 
Затем построим ступенчатую ломаную над кривой 
так, чтобы образовались прямоугольники с высотами 
и площадь:
. . . . . . .
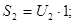
Тогда площадь всей ступенчатой фигуры
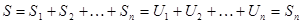– частичная сумма ряда (1).
Так как ряд с неотрицательными членами то 
не убывает при 
.
Найдем площадь криволинейной трапеции, ограниченной кривой и прямыми y=0, x=1, x=n+1, тогда
| | |||
| |
7. Определить область сходимости функционального ряда.
а) 
б) 
в) 
8. а) Разложить 
в ряд Тейлора по степеням разности 
,пользуясь определением ряда Тейлора;
б) Разложить в ряд Маклорена, пользуясь стандартными разложениями.
а) 
б)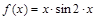 
9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).
а) 
10. а)Найти неопределённый интеграл;
б) Найти или вычислить, определённый интеграл;
в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).
а) 
б) 
в) 
11. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б) 
по синусам.
12. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б) 
по косинусам.
Вариант№24
1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.
а)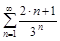 
б) 
2. Исследовать ряды на сходимость по определению сходимости.
а) 
б) 
3. Исследовать ряды на сходимость с помощью признака сравнения.
а)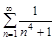 
б) 
4. То же с помощью признака Даламбера.
а)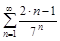 
б) 
5. То же с помощью интегрального (Коши-Маклорена) признака.
а) 
б)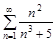 
6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.
а) 
б) 
очевидно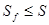 
.
Следовательно 
(2).
Построим ступенчатую фигуру под кривой y=f(x) и найдем ее площадь.
. . . . . . .
Площадь вписанной фигуры:
;
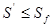, т. е. 
; 
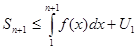(3).
Объединяя (2) и (3) получим:
.
Таким образом: 1) если 
сходится, то
, и будет ограничена для любых n сверху 
и имеет 
поэтому ряд (1) сходится, а его сумма удовлетворяет условию
| |
| |
2) если расходится, то 
, и согласно (2) возрастает при . Ряд (1) расходится.
Пример 15. Исследовать на сходимость ряд:
, 
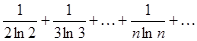По необходимому признаку
.
Следовательно, 
задача сводится к исследованию сходимости несобственного интеграла.
т. е. ряд расходится.
Пример16. Исследовать на сходимость обобщенный гармонический ряд:
,
Решение интеграла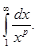 
. 
Отсюда следует, что обобщенный гармонический ряд сходится при р>1 и расходится при p£1.
| |
| ||||
7. Определить область сходимости функционального ряда.
а) 
б) 
в) 
8. а) Разложить в ряд Тейлора по степеням разности ,пользуясь определением ряда Тейлора;
б) Разложить в ряд Маклорена, пользуясь стандартными разложениями.
а) 
б)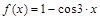 
9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).
а) 
10. а)Найти неопределённый интеграл;
б) Найти или вычислить, определённый интеграл;
в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).
а) 
б) 
в) 
11. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б) 
по косинусам.
12. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б) 
по синусам.
Вариант№23
1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.
а) 
б) 
2. Исследовать ряды на сходимость по определению сходимости.
а) 
б) 
3. Исследовать ряды на сходимость с помощью признака сравнения.
а) 
б) 
4. То же с помощью признака Даламбера.
а) 
б) 
5. То же с помощью интегрального (Коши-Маклорена) признака.
а) 
б) 
6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.
а)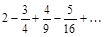 
б) 