 |
|
Предельный признак Даламбера.
Если 
Признак Коши (радикальный)
Если ряд 
с неотрицательными членами 
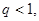что для всех достаточно больших n выполняется 
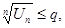то сходится, если нет 
то ряд расходится.
Доказательство:
Условие 
при 
означает, что все члены ряда кроме конечного числа их, не превосходят членов
| | |||
| | |||
ряда сходящейся геометрической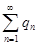 
, а, следовательно, ряд сходится.
Если то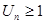 
т. е. не выполняется необходимое условие сходимости ряда. Ряд расходится.
Следствие:
Предельный признак Коши
Если существует 
то при р<1 ряд сходится; при р>1 – расходится; р=1 не ясно.
Пример 8.
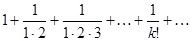, k = 1,2, …
Необходимый признак:
Проверим достаточный признак Даламбера:
Ряд сходится.
Пример 9.
по Коши (достаточный признак).
Ряд сходится.
| |
| |
7. Определить область сходимости функционального ряда.
а)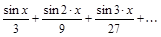 
б)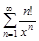 
в)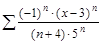 
8. а) Разложить 
в ряд Тейлора по степеням разности 
,пользуясь определением ряда Тейлора;
б) Разложить в ряд Маклорена, пользуясь стандартными разложениями.
а) 
б)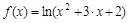 
9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).
а) 
10. а)Найти неопределённый интеграл;
б) Найти или вычислить, определённый интеграл;
в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).
а)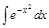 
б)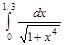 
в) 
11. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б)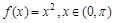 
по косинусам.
12. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б) 
по косинусам.
Вариант№26
1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.
а)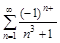 
б) 
2. Исследовать ряды на сходимость по определению сходимости.
а) 
б) 
3. Исследовать ряды на сходимость с помощью признака сравнения.
а) 
б)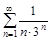 
4. То же с помощью признака Даламбера.
а)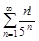 
б) 
5. То же с помощью интегрального (Коши-Маклорена) признака.
а) 
б)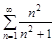 
6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.
а) 
; б) 
Пример 10.
Исследовать сходимость обобщенного гармонического ряда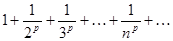 
(p – действительное число)
Необходимое условие:
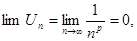
по Даламберу:
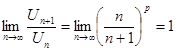
по Коши:
.
Судить о сходимости или расходимости нельзя. Необходим другой признак.
Пример 11.
Исследовать сходимость ряда.
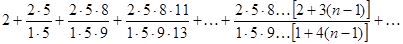
Имеем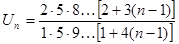 
Найдем 
Ряд сходится.
Пример 12.
Исследовать сходимость ряда.
Имеем 
| | |||
| | |||
Найдем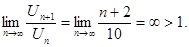 
Ряд расходится.
Пример 13.
Исследовать на сходимость ряд 
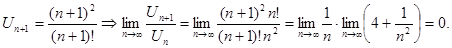
Итак,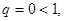 
следовательно, исходный ряд сходится.
Пример 14.
Исследовать на сходимость ряд 
Применим признак Коши:
Исходный ряд сходится.
Замечание 1.
Признак Даламбера и Коши удобно использовать, когда в общем члене ряда содержатся величины типа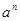 
и (или)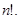 
Замечание 2.
Признаки Даламбера и Коши равносильны.
| | |||
| | |||
7. Определить область сходимости функционального ряда.
р) 
б)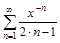 
в)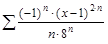 
8. а) Разложить в ряд Тейлора по степеням разности ,пользуясь определением ряда Тейлора;
б) Разложить в ряд Маклорена, пользуясь стандартными разложениями.
а)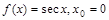 
б) 
9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).
а)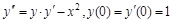 
10. а)Найти неопределённый интеграл;
б) Найти или вычислить, определённый интеграл;
в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).
а) 
б) 
в) 
11. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б)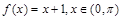 
по косинусам.
12. Разложить в ряд Фурье указанные функции в указанных интервалах.
а)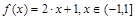 
б)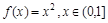 
по синусам.
Вариант№25
1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.
а) 
б) 
2. Исследовать ряды на сходимость по определению сходимости.
а) 
б) 
3. Исследовать ряды на сходимость с помощью признака сравнения.
а) 
б)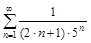 
4. То же с помощью признака Даламбера.
а) 
б) 
5. То же с помощью интегрального (Коши-Маклорена) признака.
а)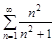
б)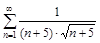 
6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.
а) 
б)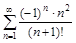 
Формула Стирлинга.
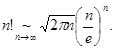
Формула Стирлинга используется для исследования на сходимость по признаку Даламбера, иногда в случае, когда признак Даламбера не работает. Так, для ряда
имеем:
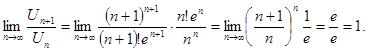
Применяя формулу Стирлинга к n-му члену ряда, имеем:
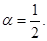
Итак, исходный ряд ведет себя в смысле сходимости как обобщение гармонического ряда с 
т. е. расходится.