 |
|
Знакопеременные ряды
Ряд, в котором члены со знаками “+” и “--” расположены в произвольной последовательности, называется знакопеременным.
Пусть имеем ряд 
(1), где знаки членов ряда произвольны. Составим из (1) ряд, состоящий из абсолютных величин ряда (1):
… (2)
Для рядов с членами произвольного знака применяют следующий достаточный признак сходимости:
Если ряд (2 )сходится, то сходится ряд(1).
Доказательство:
Очевидно, что 
(n=1, 2, …) (3).
| |
| |
можно представить как общий член сходящегося ряда.
7. Определить область сходимости функционального ряда.
а) 
б) 
в) 
8. а) Разложить 
в ряд Тейлора по степеням разности 
,пользуясь определением ряда Тейлора;
б) Разложить в ряд Маклорена, пользуясь стандартными разложениями.
а) 
б) 
9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).
а) 
10. а)Найти неопределённый интеграл;
б) Найти или вычислить, определённый интеграл;
в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).
а) 
б) 
в) 
11. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б) 
по косинусам.
12. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б) 
по синусам.
Вариант№22
1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.
а) 
б) 
2. Исследовать ряды на сходимость по определению сходимости.
а)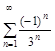 
б) 
3. Исследовать ряды на сходимость с помощью признака сравнения.
а) 
б) 
4. То же с помощью признака Даламбера.
а) 
б) 
5. То же с помощью интегрального (Коши-Маклорена) признака.
а) 
б) 
6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.
а) 
б) 
По признаку сравнения рядов: так как сходится 
(по условию), то сходится и ряд
(4),
что следует из условия (3). Тогда ряд (1) сходится, так как его можно представить в виде разности сходящихся рядов (4) и (2).
Ряд (1) называется абсолютно сходящимся, если сходится ряд (2) составленный из абсолютных величин его членов.
Замечание:
Для знакопостоянных рядов понятие сходимости и абсолютной сходимости совпадают.
Ряд (1) называется условно сходящимся, если данный ряд сходится, а ряд составленный из абсолютных величин его членов (2) расходится.
Пример 17.
Исследовать на сходимость ряд
По признаку Лейбница ряд сходится, т. к. 
, и 
.
Принимая в качестве приближенной суммы ряда его частичную сумму:
,
мы допускаем ошибку, абсолютная величина которой не больше 
.
| | |||
| | |||
Пример 18.