 |
|
Свойства сходящихся числовых рядов
Определение сходимости числового ряда основано на пределе последовательности частичных сумм. Поэтому свойства сходящихся последовательностей переносятся на числовые ряды:
3. Отбрасывание конечного числа членов ряда не влияет на его сходимость.
Необходимый признак сходимости
Теорема 1.
Если ряд 
сходится, то его общий член 
стремится к нулю, при n стремящемся в бесконечность, т. е.
| | |||
| | |||
7. Определить область сходимости функционального ряда.
а)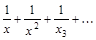 
б) 
в) 
8. а) Разложить 
в ряд Тейлора по степеням разности 
,пользуясь определением ряда Тейлора;
б) Разложить в ряд Маклорена, пользуясь стандартными разложениями.
а) 
б)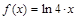 
9. Найти решение данного дифференцального уравнения в виде степенногог ряда (четыре ненулевых числа).
а) 
10. а)Найти неопределённый интеграл;
б) Найти или вычислить, определённый интеграл;
в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).
а) 
, б) 
,
в) 
11. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б) 
по косинусам.
12. Разложить в ряд Фурье указанные функции в указанных интервалах.
а) 
б) 
по синусам.
Вариант№29
1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.
а) 
б) 
2. Исследовать ряды на сходимость по определению сходимости.
а) 
б) 
3. Исследовать ряды на сходимость с помощью признака сравнения.
а)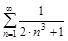 
б) 
4. То же с помощью признака Даламбера.
а) 
б) 
5. То же с помощью интегрального (Коши-Маклорена) признака.
а)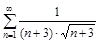 
б) 
6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.
а) 
б) 
Доказательство:
Частичная сумма (n-1) члена и n членов ряда:
, тогда
Так как ряд сходится, то
и 
.
Отсюда
Следствие
Если общий член ряда при 
, к нулю не стремится, то данный ряд расходится.
Теорема 2.
Если ряд сходится, то последовательность его частичных сумм ограничена.
Действительно, по определению сходящегося ряда, последовательность его частичных сумм имеет конечный предел, а значит, эта последовательность ограничена.
Замечание
Ограниченности последовательности частичных сумм недостаточно для сходимости ряда.
| | |||
| | |||
Гармонический ряд
расходится, хотя для него
Действительно, если бы он сходился, обладая суммой S, то мы имели бы
но
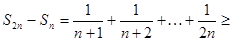
т. е.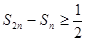 
, а это означает, что равенство 
не может иметь места.