Главная | Обратная связь

Признаки условно сходящихся рядов

1. Сумма ряда зависит от порядка слагаемых (т. е. коммутативный закон сложения не имеет место).

2. Сумма рядов зависит от того, как сгруппированы члены ряда без нарушения порядка следования (т. е. ассоциативный закон сложения не имеет место).

Например, известно, что ряд

Расходится, но, если его сгруппировать иначе

 

 

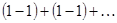, то получим .

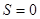Представим ряд в виде, где 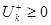, . При этом порядок следования элементов не нарушаем.

 

Свойство условно сходящихся рядов

Если ряд 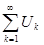сходится условно, то 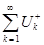и расходятся.

Пример 19.Исследовать на сходимость ряд

,

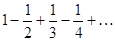по признаку Лейбница ряд сходится,а ряд, составленный из абсолютных величин

(гармонический ряд) – расходится. Следовательно, ряд условно сходящийся.

 

Пример 20. Исследовать на сходимость ряд

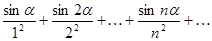(1)

Составим ряд из абсолютных величин (2)

и вспомогательный ряд (для сравнения) 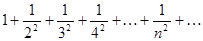. Этот ряд сходится (обобщенный гармонический ряд).

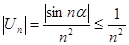Очевидно, что . Следовательно, сходится ряд (2) и абсолютно сходится заданный ряд (1).

7. Определить область сходимости функционального ряда.

а)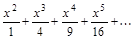

б)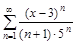

в)

8. а) Разложить в ряд Тейлора по степеням разности ,пользуясь определением ряда Тейлора;

б) Разложить в ряд Маклорена, пользуясь стандартными разложениями.

а)

б)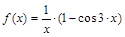

9. Найти решение данного дифференцального уравнения в виде степенного ряда (четыре ненулевых числа).

а)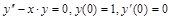

10. а)Найти неопределённый интеграл;

б) Найти или вычислить, определённый интеграл;

в) Вычислить значение указанной функции (вычисления выполнить с точностью до 0.001, затем указать точность вычисления, взяв три члена соответствующего стандартного ряда).

а)

б) 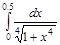; в)

11. Разложить в ряд Фурье указанные функции в указанных интервалах.

а)

б) 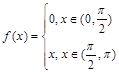по косинусам.

12. Разложить в ряд Фурье указанные функции в указанных интервалах.

а)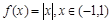

б) по косинусам.

 

Вариант№20

1.Написать пять первых членов ряда. Проверить для данных рядов выполнение необходимого признака сходимости.

а)

б)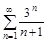

2. Исследовать ряды на сходимость по определению сходимости.

а)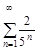

б)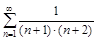

3. Исследовать ряды на сходимость с помощью признака сравнения.

а)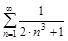

б)

4. То же с помощью признака Даламбера.

а)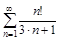

б)

5. То же с помощью интегрального (Коши-Маклорена) признака.

а)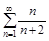

б)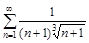

6. а) Записать общий член ряда, б) Исследовать ряды на сходимость.

а)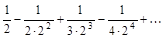

б)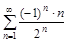

 

 

Пример 21.

Исследовать на сходимость ряд

.

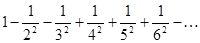Рассмотрим ряд из абсолютных величин .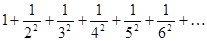

Он сходится, тогда сходится и исходный ряд, причем абсолютно.