 |
|
Векторные пространства и алгебры
Пусть дана коммутативная группа A по сложению (11,1) с элементами и, v,…, в которой, кроме сложения элементов, определено еще также умножение их на действительные числа а, b,... так, что произведение аи принадлежит группе A, где а — любое действительное число, а и — любой элемент из А.
Определение 1. Элемент и группы A называется линейной комбинацией элементов  относительно поля действительных чисел D, если в D имеются такие
относительно поля действительных чисел D, если в D имеются такие
числа  , что выполняется равенство
, что выполняется равенство

Например, каждый кватернион является линейной комбинацией четырех элементов 1, i, j, k, так как  Роль группы A здесь выполняет множество всех кватернионов.
Роль группы A здесь выполняет множество всех кватернионов.
Определение 2. Система элементов  группы A называется линейно зависимой над полем действительных чисел D, если какой - либо элемент этой системы является линейной комбинацией остальных её элементов. В противном случае система
группы A называется линейно зависимой над полем действительных чисел D, если какой - либо элемент этой системы является линейной комбинацией остальных её элементов. В противном случае система  называется линейно независимой. В частности, если зависимая система состоит только из двух элементов u и v, т. е.
называется линейно независимой. В частности, если зависимая система состоит только из двух элементов u и v, т. е.  , то элемент и называется пропорциональным элементу v.
, то элемент и называется пропорциональным элементу v.
Теорема 3. Для того чтобы система элементов  группы A была линейно зависимой над полем D, необходимо и достаточно, чтобы существовали действительные, не все равные нулю, числа
группы A была линейно зависимой над полем D, необходимо и достаточно, чтобы существовали действительные, не все равные нулю, числа  такие, чтобы выполнялось равенство
такие, чтобы выполнялось равенство

Доказательство. Пусть система элементов  линейно зависима, т. е.
линейно зависима, т. е.
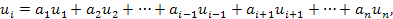
Тогда

где  .
.
Обратно, пусть  где
где  . Тогда
. Тогда

т. е. элемент  является линейной комбинацией остальных элементов.
является линейной комбинацией остальных элементов.
Эту доказанную теорему можно принять в качестве определения линейной зависимости элементов группы A относительно поля D.
Следствие 4. Для того чтобы система элементов  группы A была линейно независимой, необходимо и достаточно, чтобы равенство
группы A была линейно независимой, необходимо и достаточно, чтобы равенство

выполнялось только при условии 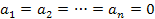 .
.
Например, равенство 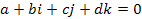 выполняется только при условии
выполняется только при условии  следовательно, система 1, i, j, k линейно независима над полем действительных чисел D.
следовательно, система 1, i, j, k линейно независима над полем действительных чисел D.
Определение 5. Линейно независимая система элементов группы A

называется базисом этой группы, если любой элемент из A является линейной комбинацией элементов данной системы. Говорят также, что любой элемент из A линейно выражается через базис данной группы.
Например, система 1, i, j, k является базисом группы кватернионов Q.
Определение 6. Коммутативная группа по сложению A называется n - мерным векторным пространством над полем действительных чисел D, если в A определено умножение элементов на действительные числа, обладающее следующими свойствами:
1)Произведение аи всегда принадлежит А.
2)  .
.
3)  .
.
4)  .
.
5)В группе A имеется базис, состоящий из n элементов

Всякий элемент n - мерного векторного пространства A называется n - мерным вектором, а число элементов базиса n называется размерностью данного пространства.
Следствие 7. Из условий 2 и 4 определения 30,6 следует:

В частности, при b = 1 и при b = 0 получаем: 
Следствие 8. Из условия 3 определения 30,6 и свойств элементов группы A следует:


т. е. сложение элементов n - мерного векторного пространства сводится к сложению соответственных компонентов (действительных чисел).
Следствие 9. Каждый элемент векторного пространства A линейно выражается через базис единственным образом (однозначно).
Доказательство. Из  следует
следует
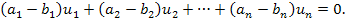
Последнее равенство ввиду линейной независимости базиса возможно тогда, и только тогда, когда все коэффициенты равны нулю, т. е.

Теорема 10. n - мерное векторное пространство A над полем D с точностью до изоморфизма однозначно определяется заданием размерности, т. е. все n - мерные векторные пространства над полем действительных чисел изоморфны друг другу.
Доказательство. Если  и
и  базисы двух n - мерных векторных пространств A и B, то изоморфным соответствием будет
базисы двух n - мерных векторных пространств A и B, то изоморфным соответствием будет

так как это соответствие взаимно однозначное и оно не будет нарушаться при сложении и умножении векторов на действительные числа.
На основании теоремы 30,10 мы можем понимать под n - мерным вектором просто упорядоченную систему n действительных чисел  Сумма двух векторов
Сумма двух векторов  тогда будет определяться как вектор
тогда будет определяться как вектор  а произведение
а произведение  — как вектор
— как вектор 
Свойства 1 — 4 определения 30,6 в определенном таким образом множестве векторов будут автоматически выполняться. Далее, в качестве базисных элементов -мерного векторного пространства  проще всего можно выбрать векторы, называемые единичными векторами:
проще всего можно выбрать векторы, называемые единичными векторами:


. . . . . . . . . . . . . . . 

Система  единичных векторов линейно независима, так как равенство
единичных векторов линейно независима, так как равенство
 будет выполняться тогда, и только тогда, когда
будет выполняться тогда, и только тогда, когда  . В этом же множестве
. В этом же множестве  выполняется и свойство 5 определения 30,6, так как для всякого вектора имеет место равенство
выполняется и свойство 5 определения 30,6, так как для всякого вектора имеет место равенство

Таким образом, множество А всех упорядоченных систем  действительных чисел на самом деле образует -мерное векторное пространство.
действительных чисел на самом деле образует -мерное векторное пространство.
Определение 30,11.  -мерное векторное пространство
-мерное векторное пространство  над полем действительных чисел
над полем действительных чисел  называется алгеброй или гиперкомплексной системой ранга
называется алгеброй или гиперкомплексной системой ранга  над полем
над полем  , если в
, если в  определено еще умножение элементов
определено еще умножение элементов  друг на друга, которое подчиняется закону ассоциативности и связано со сложением обоими законами дистрибутивности, кроме того, выполняется условие:
друг на друга, которое подчиняется закону ассоциативности и связано со сложением обоими законами дистрибутивности, кроме того, выполняется условие:
6.  для всех
для всех  из
из  .
.
Если при этом алгебра  является телом, то она называется алгеброй с делением.
является телом, то она называется алгеброй с делением.
Следствие 30,12. Из условия 6 следует равенство:
 (I)
(I)
Следствие 30,13. Из выполнения законов дистрибутивности в  следует равенство:
следует равенство:
 (II)
(II)
Последнее равенство показывает, что для вычисления произведения любых элементов из  достаточно знать произведение любых базисных элементов
достаточно знать произведение любых базисных элементов  и
и  . При этом произведение базисных элементов само должно быть линейной комбинацией базисных элементов, т. е. должно выполняться равенство:
. При этом произведение базисных элементов само должно быть линейной комбинацией базисных элементов, т. е. должно выполняться равенство:

 (III)
(III)
Таким образом, для составления таблицы умножения базисных элементов потребуется  действительных чисел (всех произведений будет
действительных чисел (всех произведений будет  , а для каждого такого произведения требуется
, а для каждого такого произведения требуется  коэффициентов), которые называются структурными константами этой алгебры.
коэффициентов), которые называются структурными константами этой алгебры.
При произвольном выборе структурных констант закон дистрибутивности следует из условий II и III. Для выполнения же закона ассоциативности умножения необходимо и достаточно еще потребовать его выполнения для базисных элементов
 (IV)
(IV)
Требования II, III, IV вместе с требованиями из следствий 7 и 8, т.е. вместе с требованиями:
 ,
,
 .
.
полностью определяют операции в алгебре  над полем
над полем  .
.
Если еще умножение базисных элементов алгебры  над полем
над полем  коммутативно, т. е.
коммутативно, т. е.  для любых элементов
для любых элементов  и
и 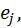 то алгебра
то алгебра  будет коммутативной алгеброй с делением.
будет коммутативной алгеброй с делением.
Примеры алгебр с делением над полем действительных чисел.
1. Само поле действительных чисел D есть алгебра ранга 1. Базис этой алгебры состоит из одного элемента — единицы.
2. Поле комплексных чисел  есть алгебра ранга 2. Базис этой алгебры состоит из двух элементов 1 и
есть алгебра ранга 2. Базис этой алгебры состоит из двух элементов 1 и 
3. Тело кватернионов есть алгебра ранга 4. Базис этой алгебры состоит из четырех элементов 1, 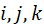 .
.
Следует иметь в виду, что в качестве базисных элементов алгебры  могут быть выбраны и другие элементы данной алгебры, но во всех случаях их число будет одно и то же, равное рангу алгебры
могут быть выбраны и другие элементы данной алгебры, но во всех случаях их число будет одно и то же, равное рангу алгебры  .
.
Мы уже видели, что поле действительных чисел Rявляется максимальным архимедовски расположенным полем, поэтому при переходе к полю комплексных чисел пришлось отказаться от выполнения аксиомы Архимеда и вместе с этим и от аксиом скалярного расположения. При переходе от поля комплексных чисел к телу кватернионов  пришлось отказаться от коммутативности умножения. Дальнейшие расширения приводят к потере других важных свойств числовых множеств, в частности закона ассоциативности умножения и других.
пришлось отказаться от коммутативности умножения. Дальнейшие расширения приводят к потере других важных свойств числовых множеств, в частности закона ассоциативности умножения и других.
Оказывается, что перечисленными тремя примерами ассоциативных алгебр с делением над полем действительных чисел  с точностью до изоморфизма исчерпываются все такие алгебры.
с точностью до изоморфизма исчерпываются все такие алгебры.
Теорема Фробениуса. Поле действительных чисел, поле комплексных чисел и тело кватернионов являются единственными с точностью до изоморфизма ассоциативными алгебрами с делением конечного ранга над полем действительных чисел R .
Доказательство. Пусть над полем Rдана ассоциативная алгебра  с делением ранга
с делением ранга  . Так как
. Так как  содержит единицу, то в
содержит единицу, то в  содержится целиком поле R или поле
содержится целиком поле R или поле  , изоморфное полю R. если
, изоморфное полю R. если 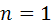 , то алгебра
, то алгебра  совпадает c Rили изоморфна R.
совпадает c Rили изоморфна R.
Если  , то для проведения доказательства, данной теоремы нам потребуется еще одно свойство -мерных векторных пространств.
, то для проведения доказательства, данной теоремы нам потребуется еще одно свойство -мерных векторных пространств.
Теорема 14. Всякие  элементов -мерного векторного пространства
элементов -мерного векторного пространства  над полем действительных чисел R составляют линейно зависимую систему.
над полем действительных чисел R составляют линейно зависимую систему.
Доказательство. Из курса высшей алгебры известно, что система однородных линейных уравнений с числом неизвестных, большим числа уравнений данной системы, всегда имеет и не нулевые решения. Пусть даны  произвольные
произвольные  элементов данного
элементов данного  -мерного векторного пространства
-мерного векторного пространства  и
и  — базис этого пространства. Тогда
— базис этого пространства. Тогда
 , ,
 ,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . ,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
 , ,
| 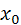
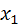 (1) (1)

|
Умножаем почленно эти равенства соответственно на некоторые действительные числа 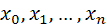 (как показано выше) и затем складываем полученные после такого умножения равенства почленно. После этого получим равенство
(как показано выше) и затем складываем полученные после такого умножения равенства почленно. После этого получим равенство

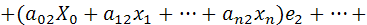
 (2)
(2)
справедливое при любом выборе множителей  Система уравнений
Система уравнений

| 
 . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . .

|
согласно сделанному в начале доказательства замечанию имеет по меньшей мере одно не нулевое решение (таких решений будет бесконечное множество)  т. е. решение, в котором не все
т. е. решение, в котором не все  при
при  равны нулю. При
равны нулю. При  из равенства (2) получается равенство
из равенства (2) получается равенство
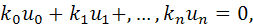
которое показывает, что, по теореме 30,3, элементы  составляют линейно зависимую систему. Теорема доказана.
составляют линейно зависимую систему. Теорема доказана.
Пусть теперь  — произвольный элемент из алгебры
— произвольный элемент из алгебры  , не являющийся действительным числом (не принадлежащий и множеству, изоморфному R). Для элементов
, не являющийся действительным числом (не принадлежащий и множеству, изоморфному R). Для элементов 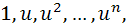 число которых равно
число которых равно  найдутся действительные числа
найдутся действительные числа  не все равные нулю, что будет выполняться равенство
не все равные нулю, что будет выполняться равенство

т.е. элемент  является корнем уравнения
является корнем уравнения

с действительными коэффициентами, степень которого не
выше  .
.
Кроме того, из курса высшей алгебры известно, что всякий многочлен с действительными коэффициентами разлагается на множители тоже с действительными коэффициентами не выше второй степени. Так как в алгебре делители нуля отсутствуют (  является телом), то элемент
является телом), то элемент  должен быть корнем некоторого квадратного уравнения
должен быть корнем некоторого квадратного уравнения

с дискриминантом, меньшим нуля (в противном случае элемент  был бы действительным числом).
был бы действительным числом).
Из 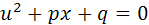 получаем:
получаем:

Таким образом, в любой алгебре  ранга
ранга  содержится по меньшей мере один элемент
содержится по меньшей мере один элемент

со свойством 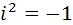 . Такой элемент будем называть мнимой единицей алгебры
. Такой элемент будем называть мнимой единицей алгебры  .
.
Если  то любой элемент алгебры
то любой элемент алгебры  будет линейной комбинацией элементов 1 и
будет линейной комбинацией элементов 1 и  , а поэтому получаем поле комплексных чисел или поле, ему изоморфное.
, а поэтому получаем поле комплексных чисел или поле, ему изоморфное.
Если  , то в алгебре
, то в алгебре  найдется элемент
найдется элемент  ,не являющийся линейной комбинацией элементов 1 и
,не являющийся линейной комбинацией элементов 1 и  и удовлетворяющий уравнению
и удовлетворяющий уравнению

тоже с отрицательным дискриминантом. Тогда элемент
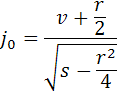
тоже будет мнимой единицей алгебры  , так как
, так как  . Элементы
. Элементы  составляют линейно независимую систему над полем действительных чисел (в противном случае элемент
составляют линейно независимую систему над полем действительных чисел (в противном случае элемент  был бы линейной комбинацией элементов 1 и
был бы линейной комбинацией элементов 1 и  ). Так как всякий элемент алгебры, не являющийся действительным числом (элементы поля, изоморфного полю R, не будем отличать от соответственных действительных чисел) удовлетворяет некоторому квадратному уравнению, то элементы
). Так как всякий элемент алгебры, не являющийся действительным числом (элементы поля, изоморфного полю R, не будем отличать от соответственных действительных чисел) удовлетворяет некоторому квадратному уравнению, то элементы  и
и  должны быть корнями некоторых уравнений
должны быть корнями некоторых уравнений

с действительными коэффициентами. Тогда из 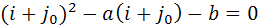
следует 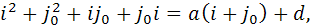 из
из 
следует 
Складывая почленно равенства


| 
| (1) |
с учетом  получим:
получим:

или
 (2)
(2)
Из последнего равенства ввиду линейной независимости элементов 1  следует
следует  , т. е.
, т. е.  . Теперь из (1) получаем:
. Теперь из (1) получаем:
 (3)
(3)
где 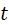 — действительное число, равное
— действительное число, равное  .
.
Положим
 (4)
(4)
Элементы  — линейно независимы над полем действительных чисел, так как из линейной зависимости между ними следовала бы линейная зависимость между
— линейно независимы над полем действительных чисел, так как из линейной зависимости между ними следовала бы линейная зависимость между  . Теперь, имея в виду равенство (3), получаем:
. Теперь, имея в виду равенство (3), получаем:

т. е. этот квадрат оказывается действительным числом, которое будет даже отрицательным. В самом деле, элемент  не является действительным числом, так как иначе уже между ним и единицей существовала бы линейная зависимость. Если бы число
не является действительным числом, так как иначе уже между ним и единицей существовала бы линейная зависимость. Если бы число  было положительным, т. е.
было положительным, т. е.

то из 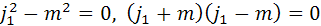 следовало бы, что алгебра
следовало бы, что алгебра  имеет делители нуля, так как
имеет делители нуля, так как  не может равняться
не может равняться  или
или  .
.
Таким образом,

где  — действительное число.
— действительное число.
Положим, наконец,

Элементы  снова будут линейно независимыми над полем
снова будут линейно независимыми над полем  , так как
, так как  отличается от
отличается от  лишь действительным множителем.
лишь действительным множителем.
Далее,

Теперь, по (3), (4), (5), получаем:

Откуда имеем:
 (6)
(6)
Положим  . Если бы элемент
. Если бы элемент  был линейной комбинацией элементов
был линейной комбинацией элементов  , т. е.
, т. е.

с действительными коэффициентами 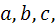 то, умножая обе части этого равенства слева на
то, умножая обе части этого равенства слева на  , мы получили бы
, мы получили бы

или

Из последнего равенства ввиду линейной независимости элементов  следовало бы
следовало бы 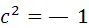 , что невозможно, так как
, что невозможно, так как  — действительное число. Таким образом, элементы
— действительное число. Таким образом, элементы  оказываются линейно независимыми, откуда вытекает, что
оказываются линейно независимыми, откуда вытекает, что 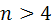 .
.
Следовательно, над полем действительных чисел алгебры ранга 3 с делением не существует.
Если  , то каждый элемент алгебры
, то каждый элемент алгебры  будет линейной комбинацией четырех элементов
будет линейной комбинацией четырех элементов 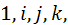 т. е. будет иметь вид:
т. е. будет иметь вид:
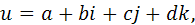
причем единичные элементы будут перемножаться по таблице умножения единичных элементов тела кватернионов.
Например, из

следуют соотношения:

и другие.
Таким образом, при  алгебра
алгебра  совпадает с телом кватернионов или изоморфна телу кватернионов.
совпадает с телом кватернионов или изоморфна телу кватернионов.
Предположим, наконец, что 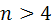 . Тогда в алгебре
. Тогда в алгебре  существует элемент
существует элемент  , не являющийся, линейной комбинацией элементов
, не являющийся, линейной комбинацией элементов 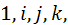 а потому в
а потому в  существует еще по меньшей мере одна мнимая единица
существует еще по меньшей мере одна мнимая единица 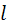 , также не являющаяся линейной комбинацией элементов
, также не являющаяся линейной комбинацией элементов  . Применяя такие же рассуждения, какими пользовались при выводе формулы (3), получим равенства:
. Применяя такие же рассуждения, какими пользовались при выводе формулы (3), получим равенства:

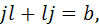

где  — некоторые действительные числа. Отсюда будем иметь:
— некоторые действительные числа. Отсюда будем иметь:

т. e.

Умножая обе части последнего равенства справа на  , получим:
, получим:

или

Откуда следует, что элемент 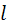 является линейной комбинацией элементов
является линейной комбинацией элементов 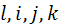 в противоречие с предположением. Следовательно, случай
в противоречие с предположением. Следовательно, случай 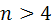 оказывается невозможным. Этим теорема Фробениуса доказана.
оказывается невозможным. Этим теорема Фробениуса доказана.
Из теоремы Фробениуса следует, что ассоциативно-коммутативных алгебр с делением над полем действительных чисел с точностью до изоморфизма существуют только две: поле действительных чисел и поле комплексных чисел. Алгебра с делением — ассоциативная, но не коммутативная, над полем действительных чисел с точностью до изоморфизма существует только одна: тело кватернионов.
Над полем действительных чисел существует ёще одна алгебра с делением, ранг которой равен 8. Но эта алгебра не является ни коммутативной, ни ассоциативной, так как законы коммутативности и ассоциативности не выполняются для ее базисных элементов 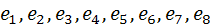 .
.
Эта алгебра называется алгеброй Кэли.
Доказано, что размерность алгебры конечного ранга с делением может равняться только  и
и  . Следовательно, при дальнейшем повышении размерности такой алгебры у нее появляются делители нуля. Поэтому деление на элементы, отличные от нуля, становится не всегда возможным.
. Следовательно, при дальнейшем повышении размерности такой алгебры у нее появляются делители нуля. Поэтому деление на элементы, отличные от нуля, становится не всегда возможным.
С этими вопросами можно подробнее ознакомиться по книге: А.Г. Курош, лекции по общей алгебре, Физматгиз, 1962.