Главная | Обратная связь

Рациональных чисел.

Основная цель настоящего параграфа – доказать следующую ниже теорему 12. Для достижения этой цели получим несколько вспомогательных результатов.

Лемма 5. Для любого положительного действительного числа α существует рациональное число r , такое , что 0< r < α.

Д о к а з а т е л ь с т в о.

Возьмем произвольное рациональное число R>0 по теореме 11, существует натуральное число N такое , что N 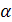> R. Тогда о < < α, и в качестве r, удовлетворяющего заключению леммы, можно взять .

Лемма 6.Если {a_n} 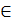α и для любого n выполняется неравенство a_n< M. Где М- рациональное число, то α≤ М.

Д о к а з а т е л ь с т в о.

Предположим противное: пусть α> М. Рассмотрим ФП { a_n- M } α –М и α –М >0. Тогда по лемме 3, существует рациональное число d > 0 и натуральное число N такие, что ( )a_n - М > d.

В таком случае ( )a_n >М, что противоречит условию, Значит , наше предположение неверно, и α≤ М.

Аналогично доказывается

Лемма 7.Если{a_n} 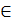α и для любого n выполняется неравенство a_n> M. Где М- рациональное число, то α≥М.

Введем понятие модуля (абсолютной величины) действительного числа:

 

На действительные числа распространяются свойства 3.1-3.8, сформулированные в §1 для рациональных чисел ( с аналогичными доказательствами). В дальнейшем мы будем пользоваться этими свойствами.

Лемма 8. Пусть α- действительное число, Если для любого ε >0 выполняется неравенство то α= 0.

Д о к а з а т е л ь с т в о.

Предположим, что α≠0. Тогда либо α> 0, либо α< 0. Если α> 0, то по лемме 5 существует рациональное число r такое, что 0 < r < α. Значит > r, что противоречит условию при . Если α< 0, то -α> 0, и, следовательно, существует рациональное число r такое, что 0 < r < -α. Но –α= , значит > r, что противоречит условию. Итак, наше предположение неверно, значит α= 0

Лемма 9.Пусть {a_n}- ФП, α- действительное число и {a_n} α. Тогда { } – ФПРЧ и { } .

Д о к а з а т е л ь с т в о.

Фундаментальность последовательности { } вытекает из фундаментальности последовательности {a_n} и из неравенства . Докажем, что } . Для этого рассмотрим три случая: α > 0, α < 0,α =0.

Пусть α > 0 . Тогда, воспользуемся теоремой 7 и леммой 3, отбросим конечное множество первых членов последовательности {a_n} и получим ФП {a_n^`} из этого же класса, состоящую из одних положительных членов. Тогда = , то есть { }

В таком случае и { } 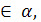ибо последовательности { } и { } отличаются лишь на конечное множество членов.

Пусть α < 0. Рассуждая аналогично, получим последовательность { , состоящую из одних отрицательных членов и такую, что { Тогда = , то есть { } ). В таком случае и { } ).

Пусть, наконец α=0. Тогда {a_n} – БМ, но и { } – БМ, значит { }

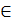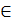
Итак, мы получили следующий результат: если α≥0, то { } α, если α < 0, то { } ). Но это значит, что { } . Лемма доказана.

Теорема 12. Пусть α- действительное число и {a_n} – ФП. Для того, чтобы {a_n} , необходимо и достаточно, чтобы ( ) ( ) ( ) . (1)

Д о к а з а т е л ь с т в о.

Необходимость.

Пусть {a_n} . Докажем, что выполняется условие (1). Возьмем произвольное число . По лемме 5, существует рациональное число r такое, что 0 < r < . Из Фундаментальности {a_n} следует

( ) ( ) ( ) r

Зафиксируем некоторое n₀ ≥ N и рассмотрим последовательность { }. По теореме 7, последовательность { } фундаментальна и эквивалентна последовательности {a_n}, значит, { } . Тогда { } - , откуда, по лемме 9 получаем { }

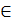
Мы имеем для любого p. Тогда по лемме 6, а потому < .

Подобное рассуждение можно провести не только для номера, но и для любого n ≥ N. Значит.

( ) ( ) (( )

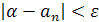
Необходимость доказана.

Достаточность.

Пусть выполнено условие (1). Докажем, что {a_n} . Прежде всего убедимся в фундаментальности последовательности {a_n}. Зададимся произвольным рациональным числом r >0. Из условия (1) следует:

( ₁) ( ₁) ( ) r/2

Тогда при ₁ (и любых p) будет выполняться неравенство r/2

Значит,

r/2+ r/2=r.

Фундаментальность последовательности {a_n} доказана.

Предположим, что – число, определяемое классом, которому принадлежит {a_n}. Возьмем произвольное

По доказанной выше необходимости имеем

( ₂) ( ₂) ε/2

Из условия (1) следует

( ₃) ( ₃) ε/2

Пусть N= max (N₁N₂). Тогда для n≥N имеем

Итак, для любого выполняется неравенство По лемме 8, отсюда следует, что . Значит {a_n} , что и требовалось доказать.

Определение 10.Говорят, что число 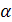является пределом последовательности {a_n} действительных чисел (и пишут ), если

(

При этом считается, что последовательность {a_n} сходится к числу Множество , в котором определено понятие сходимости последовательности, называют обычно (абстрактным ) пространством, Значит, теперь мы можем говорить о пространстве действительных чисел.

Определение 10 позволяет дать иную формулировку теоремы 12: каковы бы ни были действительное число и ФП {a_n}, условия {a_n} и равносильны.

 

§24.. Действительное число как бесконечная десятичная дробь.

Лемма 10.Для любого действительного положительного числа существует целое неотрицательное число N такое, что

N

Д о к а з а т е л ь с т в о.

По теореме 2, для чисел 1 и что K*1 Значит 0 . Рассмотрим конечное множество и выделим в нем подмножество, состоящее из всех чисел, больших 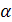. Наименьшее число из этого подмножества обозначим N+1 (оно существует по лемме1), Тогда N+1, а N α, так как N уже не принадлежит указанному подмножеству. Итак N α N+1, где N- неотрицательное целое число. Лемма доказана.

Пусть дано действительное число α>0. Построим 2 последовательности рациональных чисел, сходящихся к числу α.

По лемме10, существует неотрицательное целое число N₀ такое, что . Положим a₀= , b₀= .

Возьмем 10*α. По лемме 10, существует неотрицательное целое число N₁ такое, что N₁ 10*α

Отсюда получаем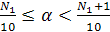

Положим

Возьмем число 100* 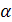, По лемме 10, существует неотрицательное целое число N₂ такое, что Отсюда получаем положим

Продолжим этот процесс. На n- м шаге рассматривается число 10ⁿ*α и подбирается целое неотрицательное N_n такое, что _.

Тогда .

Полагаем .

В итоге получаем две последовательности и , причем для любого n . Докажем, что .

Возьмем произвольное и подберем натуральное число N так, чтобы выполнялось неравенство ( это можно сделать, например, следующим образом: подбираем натуральное число k такое, что , а затем N такое, что . Тогда , а значит ). Тогда для n≥N тем более будет выполняться неравенство .

Пусть n≥N. Имеем . Таким образом, доказано следующее: . Но это означает, что .

Аналогично доказывается, что . Последовательность 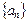назовем последовательностью десятичных приближений числа по недостатку, а - последовательностью десятичных приближений числа по избытку (аналогичное построение можно осуществить и для ).

Докажем, что - возрастающая последовательность, то есть

Сравним и . По построению , причем . Тогда 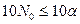. Далее, по построению , причем .

- это наибольшее целое число, не превосходящее , а - одно из целых чисел, не превосходящих . Значит, , откуда , то есть . Точно так же доказываются неравенства и т.д.

Аналогично доказывается, что - убывающая последовательность, то есть

Рассмотрим последовательность 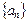несколько подробнее. Это последовательность конечных десятичных дробей, а именно, - целое число, - число с одним десятичным знаком, - число с двумя десятичными знаками и вообще - число с n десятичными знаками. Покажем, что целая часть у всех членов последовательности одна и та же. В самом деле, из возрастания последовательности получаем , то есть . С другой стороны (по построению) и, в свою очередь, . 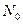Таким образом, , а это значит, что - целая часть числа .

Покажем теперь, что первый десятичный знак у всех членов последовательности, начиная с , один и тот же. Это следует из того, что у всех членов последовательности одна и та же целая часть (доказывается так же как это сделано для последовательности ).

Аналогично показывается, что второй десятичный знак у всех членов последовательности начиная с один и тот же и вообще, что n-й знак у всех членов последовательности начиная с один и то же.

Если , то - в этом случае найдем бесконечную десятичную дробь, соответствующую положительному числу - и поставим перед ней знак «минус». Это и будет бесконечная десятичная дробь, соответствующая числу . Числу 0 поставим в соответствие дробь 0,000…

Итак, каждому действительному числу ставиться в соответствие некоторая единственная десятичная дробь. Верно и обратное: каждая бесконечная десятичная дробь соответствует единственному действительному числу. Бесконечную десятичную дробь, соответствующую числу , естественно отождествить с числом (точнее, с тем символом, который мы приписали классу ФП, определяющему число ).

 

 

§25.. Полнота пространства действительных чисел.

 

Определение 11. Последовательность действительных чисел называется фундаментальной, если .

Таким образом, данное в §2 определение 3 является частным случаем определения 11.

Определение 12. Пространство называется полным, если в нем всякая фундаментальная последовательность сходится.

Теорема 13. Пространство действительных чисел полное.

Доказательство. Пусть - ФП. Построим для каждого члена этой последовательности последовательность десятичных приближений по недостатку: , , …, , …

Запишем эти последовательности в виде бесконечной прямоугольной таблицы:

: , , , , …, , …

: , , , , …, , …

: , , , , …, , …

… … … … … … … … …

: , , , , …, , …

: , , , , …, , …

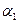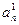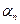Положим , , , , …, , …

Как отмечено в предыдущем параграфе . Утверждаем, что есть ФП.

Возьмем произвольное (теперь, после определения 11, число не обязательно выбирать рациональными). Подберем натуральное число так, чтобы для выполнялось неравенство . Так как - ФП, то

.

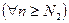
Если , то для n будут выполняться оба неравенства:

Рассмотрим . Имеем

Итак, 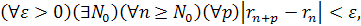а это и означает фундаментальность последовательности {r_n}.

Так как {r_n}- ФП рациональных чисел, то она принадлежит некоторому классу, определяющему число α: {r_n} .

Докажем, что

В самом деле, так как {r_n} , то по теореме 12, для произвольного 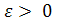имеем

Как и выше, можно найти такое натуральное N_1, .

Если положить ,то для будем иметь

Итак,

Но это и означает сходимость последовательности к числу

Нетрудно доказать и такое утверждение: всякая сходящаяся последовательность действительных чисел фундаментальна. Это фактически сделано выше при доказательстве достаточности в теореме 12 (нужно только снять требование рациональности членов последовательности). Объединив это утверждение с теоремой 12, приходим к следующему результату:

Теорема 14. (Критерий Коши)

Для того, чтобы последовательность действительных чисел была сходящейся, необходимо и достаточно, чтобы она была фундаментальной.

 

 

§26.. Заключительные замечания.

Подведем итоги сказанному в предыдущих параграфах. Построено множество действительных чисел, которые можно рассматривать как множество бесконечных десятичных дробей. Поскольку всякое рациональное число можно отождествлять с периодической или смешанно- периодической десятичной дробью, то множество Q рациональных чисел есть подмножество множества действительных чисел: Q R.

В множестве R введены операции сложения и умножения, удовлетворяющие следующим свойствам:

1.

2.

3.

4.

5.

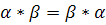
6.

7.

8.

9.

На множестве R введено отношение > , причем выполняются следующие свойства:

10. Для любого 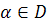имеет место один и только один из трех случаев:

11. Если то

12. Если 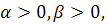то существует натуральное число N такое, что N

Наконец, для множества R определено понятие сходимости последовательности, причем выполняется следующее свойство:

13. Любая фундаментальная последовательность действительных чисел сходится:

Свойства 1) - 13) – основные свойства действительных чисел, они могут составить полный список аксиом при аксиоматическом построении множества действительных чисел.

У нас не отмечено одно из важнейших свойств множества действительных чисел – свойство непрерывности. Оно может быть получено из свойств 12) и 13) в двух формулировках: либо в формулировке Вейерштрасса – всякое бесконечное ограниченное множество действительных чисел имеет предельную точку (это сделано в книге) (2) (либо в формулировке Кантора – стягивающаяся система отрезков обладает единственной общей точкой).

 

§27. Множество комплексных чисел

Определение 1. Полем комплексных чисел C называется минимальное расширение поля R, содержащее один корень уравнения х²+1=1.

Определение 1 согласуется с принципами расширения 1-4. Действительно, при F₁=R и при F₂= C получаем:

1) RÍC

2) В C выполняются операции “+” “·”, “–” и “:” причем их смысл одинаков.

3) В С разрешимы уравнения 2-й степени, в R разрешимы только те из этих уравнений, дискриминант которых больше либо равен нулю.

4) С- минимальная система, удовлетворяющая 1-3.

Для того, чтобы доказать, что множество комплексных чисел существует, его нужно построить, то есть построить его модель.

Рассмотрим множество R´R. Оно состоит

Определение 2. Суммой комплексных чисел (a,b) и (c,d) называется комплексное число. (a,b) + (c,d) =(a+с,b+d).

Теорема 1. Алгебраическая система < C, + > является абелевой группой.

Доказательство. Из определения следует, что операция + является алгебраической на C.

1) Т.к. сложение пар покоординатно, то сложение пар обладает теми же свойствами, что и сложение действительных чисел, а значит БАО «+» ассоциативно и коммутативно на C.

2) (0,0) C является нулевым элементом в C.

3) .

Итак, <C,+> - абелева группа.Теорема доказана.

Определение 1. Произведением комплексных чисел (a,b) и (c,d) называется комплексное число (a,b) · (c,d) = (ac-bd, ad+bc).

Теорема 2. Алгебраическая система < C^♯, · > является абелевой группой.

Доказательство. Из определения следует, что операция · является алгебраической на C^♯.

1) Покажем, что операция · является ассоциативной на C^♯. Пусть (a,b), (c,d) и (k,l) C^♯.

((a,b)·(c,d)) · (k,l)=(ac-bd,ad+bc)·(k,l)=((ac-bd)k-(ad+bc)l,(ac-bd)l+(ad+bc)k)

(a,b)·((c,d) · (k,l))= (a,b)·(ck-dl,cl+dk)=(a(ck-dl)-b(cl+dk),a(cl+dk)+b(ck-dl))

Левые части равны, значит правые части равны => БАО « » ассоциативно.

II.2. Покажем, что элемент (1,0) C является единичным в C.

Действительно,

(a,b)·(1,0)= (a·1-b·0,a·0+b·1)=(a,b), аналогично,

(1,0) ·(a,b)= (a,b).

II.3. Пусть (a,b) 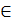C^# (т.е. (a,b) ). Покажем, что

(ax-by, bx+ay)=(1,0)

Итак,

(Этот элемент будет и левым обратным, а значит и просто обратным).

II.4. Коммутативность умножения показывается аналогично ассоциативности. Теорема доказана.

Теорема 2. Алгебраическая система < ℚ^♯,+, · > является полем.

Доказательство.

3) По теореме 1' < C, + > - абелева группа.

4) По теореме 2' < C^♯, · > - абелева группа.

3) Проверим, что в C выполняются дистрибутивные законы. Пусть (a,b), (c,d) и (k,l) C

((a,b)+(c,d)) (k,l)=(a+c,b+d)(k,l)=((a+c)k-(b+d)l,(a+c)l+(b+d)k)=

=(ak+ck-bl-dl,al+cl+bk+dk)=(ak-bl,al+bk)+(ck-dl,cl+dk)=(a,b)(k,l)+(c,d)(k,l).

Таким образом, в C выполняется правый дистрибутивный закон. Поскольку операция · является коммутативной на C, то в C выполняется и левый дистрибутивный закон.

Из 1)-3) следует, что < C^♯,+, · > - поле. Теорема доказана.

 

Чтобы показать, что C является полем комплексных чисел, необходимо:

1. поле R вложить в качестве подполя в C;

2. показать, что C содержит корень уравнения x²+1=0

Рассмотрим в C подмножество R₁={(a,0):a R}

Зададим отображение φ: R→R₁ по правилу: φ(a)=(a,0) Покажем, что φ - гомоморфизм полей:

^φ(b) и

Покажем, что - биекция:

1. Т.к. "(k,0) R₁ k R: φ(k)=(k,0), то φ – сюръекция.

2. Пусть φ(a)=φ(b) для некоторых a и b.Тогда, (a,0)=(b,0) a=b => φ – инъекция.

Итак, φ - изоморфизм. R 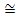R₁, R₁ – поле.

Т.к. изоморфные поля обладают одинаковыми свойствами, и с точки зрения алгебры неразличимы, то R₁ можно отождествлять с R, и, значит, можно считать, что К является подполем C, отождествляя (a,0) a, .

Покажем, что (0,1) является корнем уравнения x²+1=0. Обозначим i=(0,1) и назовем его мнимой единицей, тогда,

i²=(0,1) (0,1)=(0 0-1 1, 0 1+1 0)=(-1,0) -1 => i – корень уравнения (1). Следовательно, C удовлетворяет определению поля комплексных чисел.

Кватернионы

Множество М всех матриц вида , где а и b — любые действительные числа, представляет собой поле, изоморфное полю комплексных чисел C. Это поле содержит в себе подполе всех матриц вида , изоморфное полю действительных чисел R.

Таким образом, поле матриц M является одной из интерпретаций поля комплексных чисел C. Поэтому можно было бы к полю комплексных чисел прийти, отправляясь от поля матриц М. Этой возможностью воспользуемся для построения расширения поля комплексных чисел. Для этой цели рассмотрим множество всех матриц вида , где - любые комплексные числа, а числа — сопряженные числам бив.

Сложение и умножение этих матриц производятся по известным правилам действий над матрицами, т. е.

Две матрицы называются равными тогда, и только тогда, когда

Известно, что сложение квадратных матриц коммута­тивно и ассоциативно, умножение этих матриц ассоциативно и связано со сложением правым и левым законами дистрибутивности. Для каждой матрицы существует ей противоположная матрица такого же вида.

Перечисленные свойства показывают, что множество является кольцом.

Если же эти свойства матриц не считать известными, то легко можно проверить выполнение аксиом кольца в множестве непосредственными вычислениями по вышеуказанным правилам.

В кольце Q закон коммутативности умножения, вообще говоря, не выполняется, например

Определитель матрицы из кольца Q будет равным нулю тогда, и только тогда, когда так как из следует а = b = с = d = 0. Обратное утверждение очевидно. Из этого следует, что для каждой матрицы из ,кроме нулевой, существует обратная матрица.

Таким образом, в множестве матриц выполняются все аксиомы тела

Тело содержит в себе множество всех матриц вида , где - любые действительные числа, т. е. содержит в себе поле, изоморфное полю комплексных чисел C. Поэтому существует тело Q, являющееся расширением поля комплексных чисел C, изоморфное телу матриц .

Чтобы построить тело Q, достаточно в множестве матриц произвести замену элементов подмножества , изоморфного полю действительных чисел D, соответственными действительными числами, т. е. каждую матрицу вида заменить действительным числом а. Покажем это.

Каждая матрица

из однозначно определяется четверкой действительных чисел (a, b, с, d), причем единичная матрица определяется четвёркой (1, 0, 0, 0). Рассмотрим ещё матрицы, определяемые четвёрками чисел (0, 1, 0, 0), (0, 0, 1, 0), (0, 0, 0, 1), т. е. матрицы

Каждую матрицу из множества можно представить в виде

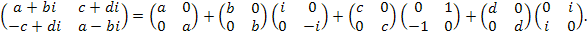
Если все элементы поля 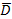заменим соответственными им при изоморфизме действительными числами, а для матриц

введем обозначения соответственно через i, j, k, то матрица

заменится выражением

Определение 1. Выражение вида , где а, b, с и d — любые действительные числа, называется кватернионом. Множество всех кватернионов называется телом кватернионов.

Название «кватернион» происходит от латинского слова quaterni — по четыре. Действительные числа a, b, с, d, однозначно определяющие кватернион , называются компонентами или координатами этого кватерниона. Сложение кватернионов сводится к сложе­нию соответственных компонентов. Элементы 1, i, j, k называются единицами тела кватернионов, причем последние три — мнимыми единицами. Чтобы получить правила умножения кватернионов, необходимо и достаточно установить это правило для умножения еди­ниц. Правила умножения единиц тела кватернионов с не­обходимостью вытекают из умножения соответственных матриц. Из равенств:

следуют равенства:

Далее следуют равенства:

Кроме того, имеем:

Из всех перечисленных равенств следует таблица умножения единиц тела кватернионов Q (черт.8)

	1	i	j	k
1	1	i	j	k
i	i	- 1	k	-j
j	j	- k	- 1	i
k	k	j	- i	- 1

 

Правило умножения кватернионов состоит в том, что их перемножают как обычные многочлены, т. е. каждый член первого кватерниона б умножают на каждый член
второго кватерниона в с учетом таблицы умножения единиц (черт. 7) и полученные
произведения складывают, применяя при этом соответствующие аксиомы кольца.
При умножении кватернионов надо строго соблюдать порядок следования сомножителей, так как умножение в множестве Q, вообще говоря, не коммутативно.

 

 

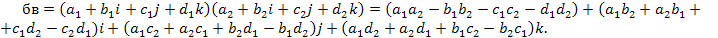
(1)

Произведение вб будет отличаться от произведения бв только тем, что во всех коэффициентах при i, j, k послед­ние два слагаемых изменят знаки на противоположные.

Определение2. Два кватерниона называются сопряженными друг другу. Произведение сопря­женных кватернионов называется нормой каждого из этих кватернионов. Норма кватерниона б обозначается через N (б).

Если в равенствах (1) положим

то получим, что

Точно так же получается, что

Отсюда следуют равенства:

(2)

Следствие 3. Кватернион тогда, и только тогда, равен нулю, когда его норма равна нулю.

Следствие 4. Если в произведении кватернионов вб оба сомножителя заменить кватернионами, им сопря­женными, то получится кватернион, сопряженный произведению бв, т. е. для кватернионов имеет место равенство

. (3)

Для доказательства достаточно вычислить про­изведение и сравнить его с произведением бв.

Следствие 5. Норма произведения кватернионов равна произведению норм сомножителей.

Доказательство.

(4)

Так как множество кватернионов Q является телом, то для каждого кватерниона существует ему обратный кватернион , потому что

Уравнение при решается путем умножения обеих его частей слева на т. е

Для уравнения умножаем обе его части справа на и получаем:

Множество 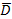всех кватернионов вида представляет собой поле, изоморфное полю всех действительных чисел D т. е. 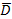является под полем тела кватернионов. В множестве Q содержатся еще три подполя, изоморфные полю комплексных чисел К: мно­жество всех кватернионов вида ,множество всех кватернионов вида и множество всех кватернионов вида .

Тело кватернионов было построено в середине XIX века английским математиком Гамильтоном в результате поисков расширения поля комплексных чисел. Уже Гамиль­тоном были найдены возможности применения кватернионов в геометрии и физике.

Различные конкретные истолкования (интерпретации) показывают возможность применения кватернионов в ма­тематике, физике, механике. Всякий кватернион можно рассматривать как состоящий из двух частей: число а называют скалярной частью, а выражение — векторной частью кватерниона . Множество v всех векторных частей кватернионов, т. е. множество всех кватернионов вида представляет собой коммутативную группу по сложению, так как сложение в этом множестве является алгебраической операцией, удовлетворяющей всем аксиомам указанной группы (§ 11). Эта группа изоморф­на группе всех обычных векторов трехмерного простран­ства, употребляемых в геометрии, физике, механике. При этом каждому кватерниону ставится в соответствие вектор Поэтому каж­дый вектор можно рассматривать как геометрическую интерпретацию кватерниона

т. е. рассматривать обычные векторы множества и элементы множества v как различные истолкования одного и того же понятия.

Умножение в множестве v не является алгебраической операцией, так как произведение двух элементов из v, вообще говоря, будет кватернион с отличной от нуля скалярной частью и тем самым не будет принадлежать множеству v. Однако и в этом случае обнаруживается тесная связь кватернионов с обычными трехмерными векторами. Перемножим два кватерниона

Первое слагаемое этого произведения представляет собой скалярное произведение векторов и , взятое с противо­положным знаком, а остальная часть этого произведения совпадает с векторным произведением и , т. е. спра­ведливо равенство:

(5)

где в левой части — кватернионы , а в правой части — соответствующие им векторы и Равенство (5) показывает связь умнож