Главная | Обратная связь

Тапшысымен тасымалдау есебі 17 страница

2-есеп. Берілген функцияның 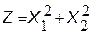-экстремалдық мәнін мына жағдайда: Х₁+Х₂=5 іздеңіз. Есептің шешімін талдаңыз.

3-есеп. Шаруа қожалығы шаруашылықтың диірменінен тар-тылған ұнды өздері нарыққа қойып, сатып және бір бөліктерін сауда агентіне көтерме бағамен (оптом) өткізе алады. Егер шаруа қожалығы Х₁ кг ұнды өздері нарыққа қойып, сатса, онда 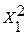ақша өлшеміндей, ал Х₂ кг ұнды сауда агентіне көтерме бағамен өткізсе, 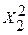ақша өлшеміндей шығын шығарады.

Күніне 5000 кг ұн дайындалған жағдайда, осы ұнды сатуға кеткен барлық шығын аз болу үшін, шаруа қожалығына әрбір ұнды сату технологиясымен қанша мөлшерде ұнды сатуға өткізгені тиімді.

4-есеп. Кәсіпорын екі түрлі шикі заттардан және бірнеше жұмысшылардың қатысуымен екі түрлі өнім өндірмекші.

Кәсіпорынының қаржы бөлімінің мамандары кейінгі он жыл-дық мәліметтер арқылы өндірілетін өнімдердің (x₁, x₂) мөлшеріне байланысты мынадай түрде табыстың (Z) эмпириялық моделін тұрғызды:

Z=11x₁+16x₂ + 0,1 + 0,12 +0,22 x₁ x₂→ max

Қорлар	Қорлар шығындары	Қорлар мөлшері
1-өнім	2-өнім
1-шикізат
2-шикізат
Еңбек шығыны

 

Өндірілетін өнімдердің бір бірлігіне есептелген аталған қор-лар шығыны және олардың кәсіпорнындағы мөлшері (өз өлшем бірлігімен) төменгі кестеде берілген.

Кәсіпорынға өндірістің берілген жағдайында максимальды табыс табу үшін әрбір өнімді қанша мөлшерде өндірген тиімді.

5-есеп.Сүт зауыты үш түрлі сүт өнімдерін (қаймақ, сыр және ірімшік) жергілікті нарққа шығарады. Күнде екі фермадан зауытқа сүт әкелінеді. Өндірілген өнімдердің технологиялық және экономи-калық мәліметтері төменгі кестелерде берілген.

 

Өнімдер	1 кг сүттен алынатын өнімдердің коэффициенті	Сөткесіне өндірілетін өнімдердің максималь-ды мөлшері, кг	Өнімдердің 1 кг құны, теңге
1-ферма	2-ферма
Қаймақ	0,1	0,2
Ірімшік	0,25	0,1
Сыр	0,1	0,08

 

Шикі затты (сүтті) сатып алуға кеткен шығындар, олардың сатып алынған мөлшеріне байланысты төменгі кестелерде үзікті-сызықты функция түрінде беріледі.

А) 1-ферма үшін

Мөлшері, кг	y1=0	y2=200	y3=300	y4=500	y5=600
Шығын, теңге

Б) 2-ферма үшін

Мөлшері, кг	z1=0	z2=200	z3=300	z4=600
Шығын, теңге

 

Есептің мақсаты сүт зауыты күнделікті жұмысында максималды пайда табуы керек.

Ескерту: Зауыттың күнделікті сатып алатын сүт мөлшері: x₁–1-ші фермадан, кг; x₂–2-ші фермадан, кг; Осыдан кейін төмендегідей үзікті-сызықты функция құрылады:

x₁= u₁ + u₂ + u₃ + u₄, мұндағы 0 ≤ u_i ≤ y_i+1–y_i

(біздің жағдайда 0 ≤ u₁ ≤ 200, 0 ≤ u₂ ≤ 100, 0 ≤ u₃ ≤ 200, 0 ≤ u₄ ≤ 100),

x₂= v₁ + v₂ + v₃ , мұндағы 0 ≤ v_i ≤ z_i+1– z_i

(біздің жағдайда 0 ≤ v₁ ≤ 200, 0 ≤ v₂ ≤ 100, 0 ≤ v₃ ≤300),

Онда 1-фермадан сатып алынатын сүттің құны мынадай функциямен жазылады: С₁(x₁) = 25 u₁ + 30u₂ +30 u₃ +35 u₄,

2-фермадан сатып алынатын сүттің құны мынадай функциямен жазылады: С₂(x₂) = 20v₁ + 30v₂ +35v₃ .

Осы ескертулерді ескеріп, келесі кезекте есептің сызықтық моделін құрңыз да, оны MS Excel көмегімен шығарыңыз.

 

 

7.4 Бүтін санды және бульдік айнымалы