 |
|
Тапшысымен тасымалдау есебі 15 страница
(6.20)
(6.20) өрнегін (6.17) формулаға енгізгеннен кейін оңтайлас-тыру есебінің моделі құрылады. Арнайы программалар пакеттерін қолдану арқылы (біздің жағдайда EUREKA программасы қолда-нылды) есепті шығардық. Есептің шешім нәтижесі бойынша np= =13,08 кезде ТҚК (ш.ө.б.) оңтайлы жүргізу аралықтары Lжж= 15,3 мың км. Осы жағдайда жалпы шығын сомасы S = min болуы қам-тамасыздандырылады.
Қарастырылып отырған есеп мәні күтілген критерия бойын-ша шығарылды. Егер бір шешім бірнеше рет қолданылатын болса, тек осы жағдайда мәні күтілген критерия шешімді дәлме-дәл бағалайды. Егер есептің алғашқы деректері сұрыптап алынған көрсеткіштердің параметрлері болса, онда мәні күтілген критерия қате нәтиже көрсетуі мүмкін. Мұндай жағдайларда қарастырылып отырған есепті шығаруға арналған бірнеше тәсілдер бар екені жоғарыда аталды. Осы жерде оларды тереңірек оқып, зерделеу үшін мына әдебиеттерді [1, 2] оқуды ұсынамыз.
6.1.3 Анықталмаған жағдайда шешімдер қабылдау
Егер ортаның мүмкіндігі толық анықталмаған (яғни біз әрбір бастапқы мәліметтердің мүмкін бола алатын ықтималдығын тіпті жуықтап көрсете алмасақ), онда шешімді таңдау кезіндегі жағдай-ды стратегиялық ойын түрінде бейнелейді. Онда бір ойыншы – шешім қабылдайтын адам (ШҚА), ал екіншісі – объективтік шындық, ол «табиғат» болып есептелінеді. Мұндай ойындардың шартын төмендегі шешімдер кестесі арқылы көрсетуге болады.
| S1 | S2 | ... | Sn | |
| R1 | a11 | a12 | ... | a1n |
| R2 | a21 | a22 | ... | a2n |
| ... | ... | ... | ... | |
| Rm | am1 | am2 | ... | amn |
Кестедегі R1, R2, ..., Rm – жолдары ШҚА стратегияларын, ал S1, S2, …, Sn – бағаналары «табиғат» стратегиялары (aij–Ri – жолы-мен Sj - бағанасының қилысындағы ШҚА нәтижелілігінің шамасы).
Сөйтіп, шешімдер қабылдау есептерінің математикалық мо-делі табиғат қалыптарының {Sj} көптігімен, стратегия жоспар-ларының {Ri} көптігімен және мүмкін бола алатын нәтижелер ма-трицасымен ||aij|| анықталады. Кейбір есептерде нәтижелілік ретін-де тәуекелдік матрицасы қарастырылады ||rij||.
Тәуекелдік (риск), нақтылы стратегияларды қабылдауда мүм-кін бола алатын әртүрлі нәтижелердің арасындағы сәйкес келмеу-шіліктің өлшемі.
Тәуекелдіктер матрицасының элементтері нәтижелілік (пай-далылық, ұтымдылық, шығын, шығыс) элементтер матрицасымен келесідей байланыста:
rij= aj – aij (6.21)
мұндағы 
– пайдалылар матрицасының j-бағанасындағы
максимальды элемент.
Егер мүмкін болатын нәтижелілік матрица ||aij|| шығындар матрицасы болса, онда тәуекелдіктер матрицасының элементтерін келесі формуламен анықтайды:
Rij= aij – ai (6.22)
мұндағы 
– шығындар матрицасының j-бағанасындағы
минимальды элемент.
Сонымен, егер «табиғаттың» нақтылы қалпын білсек, онда осы қалыптағы нәтижемен j-стратегияда алынған нәтиженің айы-рымы тәуекелдік деп аталады.
Анықталмаған ситуацияда тәуекелдік матрица ұтымдылық (пайдалылық) матрицасына қарағанда зерделеніп отырған объектіні көрнекі суреттейді.
Қарастырылып отырған ситуацияларда ең ұтымды шешімді {R1, R2, ..., Rm} көптіктен таңдаған кезде төмендегі критериялар қолданылады:
1. Максимакстық критерия, немесе шеткі үміттілік (опти-мизм) критериясы – әрбір альтернативтер үшін максимальдық нәтижелерді максимальдайтын альтернативті анықтайды, яғни ШҚА i0 стратегиясын таңдайды, ал ол сәйкес:
2. Вальда-ның максиминдық критериясы, немесе шеткі түңілушілік (пессимизм) критериясы - әрбір альтернативтер үшін минимальдық нәтижелерді максимальдайтын, альтернативті анық-тайды, яғни ШҚА i0 стратегиясын таңдайды, ал ол сәйкес:
3. Сэвидж-дың минимакстық критериясы. Бұл критерия бойынша, ең нашар жағдайда тәуекелділіктің шамасы rij мини-мальды болатын, стратегия таңдалады, яғни ол тең:
мұндағы тәуекелдік 
4. Гурвиц-тің үміттілік - түңілушілік критериясы – ол шешім таңдаған кезде шеткі үміттілік критериясында және шеткі түңілушілік критериясында қолданбауды ұсынады. Бұл критерия бойынша, шешім стратегиясы мына шарт арқылы қабылданады:
мұндағы k түңілушілік коэффициенті, оның мәні нөлмен бірге дейін болуы мүмкін. Егер k =1 болса, онда Гурвиц формуласы Вальд формуласы түріне өзгереді, ал k >0 – шеткі үміттілік критериясына ауысады.
5. Лаплас (талғаусыз) критериясы. Толық айқын емес болған жағдайда, ортаның барлық мүмкіндігі (табиғаттың) тең ықтималды деп есептелінеді. Бұл критерия максимальды орташа нәтижелі альтернативті (стратегияны) анықтайды, яғни:
Егер қойылған шарттардың бағаларымен және ортаның бар-лық мүмкін бола алатын қалыптары ықтималдықтарының шешім-дер кестесі белгілі болса, онда әрбір альтернативтерді бағалау нәтижесінде олардың объективті EMV күтілетін бағасын анық-тауға болады. Альтернативтерді таңдау критериялардың ішіндегі ең көп таралғаны – максимальды EMV.
Әрбір альтернетивтер үшін барлық мүмкін болатын бағалар шарттарын (ұтыстарды) осы ұтыстардың ықтималдығына көбейт-кеннен кейінгі олардың сомасы арқылы сол альтернетивтердің EMV күтілетін бағасы алынады, яғни:
EMV= 
aij– i-альтернативті таңдағанда және ортаның j-қалыпындағы
ШҚА ұтысының шамасы;
pj – ортаның j-қалпының пайда болу ықтималдығы.
Анықталған жағдайдағы ұтыс шамасымен тәуекелдік жағдай-дағы ұтыс шамаларының айырымын нақтылы ақпараттардың EMVI күтілетін құндылығы деп атайды.
EMVI анықтау үшін, шешім қабылдау алдында бізде нақтылы дәйектелген ақпарат болған және анықталған жағдайда, күтілетін (орташа) табысқа тең, біріншіден математикалық күтілетін шама есептелінеді.
Нақтылы ақпараттар белгілі болса, күтілетін ұтыс шамасы былай анықталады:
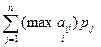
Одан
EMVI=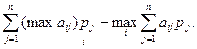 
Ортаның қалпы туралы бір көптік және альтернативтік ше-шімдер туралы бір көптігі бар есептерді талдаған кезде, шешімдер кестесін пайдаланған ыңғайлы. Бірақ көптеген есептер ортаның қалыптарынан және бірінен кейін бірі орындалатын шешімдерден тұрады. Егер есепте, екі және одан да көп бірінен кейін бірі орындалынатын шешімдер байқалса және алдыңғы шешім одан кейінгіге алғашқы деректер ретінде қолданатын болса, онда шешімдер ағашын құруға тура келеді.
Альтернативтік шешімдер, ортаның қалыптары, сонымен қатар кез келген альтернативтер және орта қалыптарының бірлес-кен комбинацияларының ықтималдықтары мен ұтыстары бейне-ленген шешімдер үрдісін графикалық түрде бейнелеу – шешімдер ағашы делінеді.
Шешімдер ағашы көмегімен есептерді талдау бес кезеңнен тұрады:
– есепті қалыптастыру (формулировка);
– шешімдер ағашын тұрғызу;
– орта қалыптарының ықтималдығын бағалау;
– әрбір мүмкін бола алатын альтернативтер және орта қа-лыптарының бірлескен комбинациялары үшін ұтыстарды тағайындау;
– орта қалыптарының әрбір төбелері үшін EMV күтілетін бағасын есептеу арқылы есепті шешу.
Бір мысал қарастырайық.
Мысал.Жоспарланған аралықта транспорттық қызмет көрсету жөнінде клиенттерінің сұранысын қанағаттандыру үшін бір транспорттық кәсіпорын өзінің тасымалдау мүмкіндік деңгейін анықтамақшы делік.Транспорттық қызметке сұраныс белгісіз, бірақ болжау жүргізу нәтижесінде ол мына төрт мәннің біреуі болатыны (10, 15, 20 немесе 25 мың тонна) анықталды. Сұраныстың әрбір деңгейі үшін кәсіпорынның ең тиімді (мүмкін болатын шығын мөлшері бойынша) тасымалдау мүмкіндік деңгейі болатыны да ескерілді. Бұл деңгейлерден ауытқу қосымша шығынға әкелетіні, ал ол сұранысқа қарағанда тасмалдау мүмкіндіктерінің артық болуынан (кейбір транспорттардың жұмыссыз босқа тұруынан) немесе транспорттық қызмет көрсетуде клиенттердің сұранысын қанағаттандыра алмаудан болуы мүмкін.
Төменде тасымалдау мүмкіндіктерінің дамуына байланысты шығындардың мүмкін болатын болжанған мәндерін анықтайтын кесте берілген.
| Кәсіпорынның тасмалдау мүмкіншіліктері | Транспорттық қызметке сұраныс нұсқалары | |||
Оңтайлы стратегияны таңдау қажет.
Шешімі
Есептің шарты бойынша, төрт нұсқа транспорттық қыз-метке сұраныс, ал ол дегеніміз «табиғаттың» төрт қалпына сәйкес келеді: S1, S2, S3, S4. Сонымен қатар кәсіпорынның тасымалдау мүмкіндіктерінің төрт стратегиясы белгілі: R1, R2, R3, R4. Тасымалдау мүмкіндіктерінің дамуына байланысты әрбір жұптар: Si және Ri үшін шығындар келесідей матрица түрінде берілсін:
| S1 | S2 | S3 | S4 | ||
| R1 | |||||
| aij = | R2 | ||||
| R3 | |||||
| R4 |
Лаплас принципі бойынша S1, S2, S3, S4 тең ықтималдылар. Олай болса, 
және әртүрлі іс-әрекетте R1, R2, R3, R4 күтілетін шығындар:
EMV{R1}= 0,25·(6 +12 +20 + 24) = 15,5;
EMV {R2}= 0,25·(9 + 7 + 9 + 28) = 13,25;
EMV {R3}= 0,25·(23 +18 + 15 + 19) = 18,75;
EMV {R4}= 0,25·(27 + 24 +21 + 15) = 21.75.
Сонымен, Лаплас критериясы бойынша тасымалдау мүмкін-діктерінің даму стратегиясының ең ұтымдысы R2.
Енді есепке Вальда критериясын қолдану жолын қарасты-райық. Бұл критерияны қолдану, оқылып отырған оъектінің ықти-малдық қалпы туралы Si ақпараттарды қажет етпейді. Онда ең нашар страгиялар Rj ішінен ең жақсысын таңдау көзделуіне бай-ланысты, ол «абай болу» принципіне сүйенеді.
Егер алғашқы нәтижелер матрицасы (есептің шарты бойынша) aij, шешім қабылдаушыға шығындарды білдірсе, онда оңтайлы стратегияны(альтернативті) таңдауға минимакстық критерия қа-былданады. Оңтайлы стратегияны Rj анықтау үшін нәтижелік матрицаның әрбір жолдары бойынша ең үлкен элементтерді табу керек 
, одан кейін осы ең үлкен элементтердің ішінен ең кішісі таңдалынады, яғни мынадай әрекет жасалынады:
Егер алғашқы нәтижелер матрицасы (есептің шарты бойынша) aji шешім қабылдаушыға ұтыстардың пайдалылығын білдірсе, онда оңтайлы стратегияны (альтернативті) таңдауға максиминдік крите-рия қабылданады. Оңтайлы стратегияны Rj анықтау үшін нәтиже-лілік матрицаның әрбір жолдары бойынша ең кіші элементтерді табу керек 
, осыдан кейін осы ең кіші элементтердің ішінен ең үлкені таңдалынады, яғни мынадай әрекет жасалынады:
Біздің мысалда, алғашқы нәтижелілік матрицада (есептің шарты бойынша) aij шешім қабылдаушының шығынын білдіреді. Сондықтан оңтайлы стратегияны таңдауға минимакстық критерия-ны қолданған ұтымды. Ол үшін жүргізілген есептеулер келесі кестеде келтірілген:
| Rj-стратегиялар | Si-қалыптары және aji –шығындар, а.ө.б. |
|
| |||
| S1 | S2 | S3 | S4 | |||
| R1 | - | |||||
| R2 | - | |||||
| R3 | ||||||
| R4 | - |
Сонымен, минимакстық критерия «нашарлар арасындағы ең жақсысы» бойынша тасымалдау мүмкіндіктерінің даму стратегия-сының ең ұтымдысы R3.
Өзінің шектен тыс шеткі түңілушілік (пессимизм) критерия-сы болуына байланысты, Вальда критериясы кейде логикадан тыс тұжырымға алып келеді. Бұл критерияның мұндай «түңілушілігін» (пессимистичности) Сэвидж критериясы жөндейді.
Сэвидж критериясы тәуекелдік матрицасын ||rij|| қолданады. Осы матрицаның элементтерін (6.21) және (6.22) формулалар арқылы анықтап, олар келесідей қалыпқа келтіріледі:
(6.23)
Формуладағы өрнектер мынаны білдіреді: rij – дегеніміз ең жақсыj –бағанадағы мәндермен j–бағанасындағы aji элементтердің айырымы. Сонымен қатар aij элементтері табыстар (пайдалар), жоқ әлде шығындар ма, онысына қарамастан rij екі жағдайда да, шешім қабылдаушыға, шығындар шамасын анықтайды. Сөйтіп, rij матри-цасына тек минимакстық критерияны қолдануға болады. Сэвидж критериясы, анықталмаған жағдайда, ең нашар ситуацияда (тәуе-келдік максимальды болғанда) тәуекелдік шамасы ең төменгі мәнді қабылдағандағы стратегияны таңдауды ұсынады.
Қарастырылып отырған мысал бойынша (6.23) формуламен ||rij|| матрицаның элементтерін есептейміз:
| S1 | S2 | S3 | S4 | ||
| R1 | |||||
| ||rij|| = | R2 | ||||
| R3 | |||||
| R4 |
Кестеде алынған нәтижелер Сэвидждің минимальдық тәуе-келдік бойынша есептелген. Осы кестені келесідей формаға түр-лендірейік:
| Rj-стратегиялар | Si-қалыптары және aji –тәуекелдік шамасы, а.ө.б. |
|
| |||
| S1 | S2 | S3 | S4 | |||
| R1 | ||||||
| R2 | - | |||||
| R3 | - | |||||
| R4 | - |
Сонымен, тәуекелдік шамасын rij енгізу, ең нашар ситуацияда (тәуекелдік максимальды болғанда) өте аз шығынды қамтамасыз ететін, бірінші стратегияны R1 таңдауға алып келді.
Стратегияларды таңдағанда Сэвидж критериясын қолдану кез келген жолмен үлкен тәуекелдіктен аулақ болуға мүмкіндік береді, яғни ол үлкен шығынға ұшыраудан сақтандырады.
Гурвица критериясы екі жағдайға негізделген: (1– α) ықти-малдықпен «табиғат» өте нашар ұтымсыз қалыпта және α ықти-малдықпен өте ұтымды қалыпта тұруы мүмкін, мұндағы α– сенім коэффициенті. Егер aij – пайда, пайдалығы, табыс және т.б.с.с., онда Гурвица критериясы былай жазылады:
(6.24)
Егер aij – шығын, шығыс және т.б.с.с., онда Гурвица критериясы былай жазылады:
(6.25)
Егер α = 0, онда Вальда-ныңмаксиминдық критериясы, немесе шеткі түңілушілік (пессимизм) критериясынқолданамыз.
Егер α = 1, онда максимакстық критерия, немесе шеткі үміттілік (оптимизм) критериясын, яғни мына түрдегі 
максимальдық нәтижелерді максимальдайтын критерияны аламыз.
Гурвица критериясы шеткі түңілушілік (пессимизм) крите-риясымен шеткі үміттілік (оптимизм) критериясы арасына, оларға сәйкес салмақтарды: (1– α) және α, өлшеу арқылы, баланс тұр-ғызады. Мұндағы α мәні, мына аралықта 0 ≤ α ≤1 жатады. Шешім қабылдаушы адамның (ШҚА) кәсіптік ыңғайына (пессимизмге, жоқ әлде оптимизмге ме) қарай α–ның мәні 0 ден 1 аралығында анық-талынады. ШҚА тәжірибесі жоқ, дағдыланбаған болса, онда α = 0,5 деп қабылдау ең дұрыс шешім болып есептелінеді.
Қарастырылып отырған мысалымызға көшейік. Айталық, α= = 0,5. Керекті есептеулер нәтижелері келесі кестеде келтірілген:
| Wi | 
| 
| 
| 
|
| W1 | ||||
| W2 | 17.5 | - | ||
| W3 | - | |||
| W4 | - |
Есептің шешім нәтижесі бойынша оңтайлы Wi таңдау.
Сонымен, мысалда қандай шешім басқаларына қарағанда ұтымдырақ екенін дәйектеп, оңтайлы шешімді таңдау нәтижесінде:
– Лаплас критериясы бойынша – R2 – стратегиясы таңдалды;
– Вальда критериясы бойынша – R3– стратегиясы таңдалды;
– Сэвидж критериясы бойынша – R1– стратегиясы таңдалды;
– Гурвица критериясы бойынша, α = 0,5 болғанда – R1– стра-тегиясы, ал егер ШҚА пессимист болса (α = 0), онда R3– стратегиясы таңдалады.
Анықталмаған жағдайда шешімдер қабылдауда критерияны таңдау әрекеттерді зерттеудің ең күрделі және жауапты кезеңдері болып саналады. Осыған байланысты берілетін жалпы кеңес немесе ұсыныс осы уақытқа дейін болған емес. Өзінің интуициясына және өткен тәжірибесіне сүйеніп, сонымен қатар өзінің қойған мақса-тына сәйкес және шығарылатын есептің нақтылы спецификасын ескеріп, критерияны шешім қабылдайтын адам таңдауға тиіс.
Кейбір жағдайларда, егер минимальдық тәуекелдікті қабыл-дауға рұқсат жоқ болса, онда Вальда критериясын қабылдаған жөн. Керісінше жағдайда, яғни ШҚА бірәз мөлшерде тәуекелдікті қабылдай алса және өкінбейтіндей мөлшерде кейбір кәсіпорынды қаржыландыра алатындай болса, онда Сэвидж критериясын таңдаған ұтымды.
Сонымен, шешімдер қабылдау теориясының негізін қысқаша баяндауды осымен аяқтаймыз. Шешімдер қабылдау теориясымен тереңірек танысқысы келетін оқырмандарға мына әдебиеттерді [1, 2 және т.б.] оқуды ұсынамыз.
7. Оқушылардың өзіндік жұмыстарына арналған есептермен тапсырмалар
7.1 Сызықтық модельдерге есептер
1-есеп.Кәсіпорында 3500 м2 егіске көкөніс өндірілмекші. Барлық көкөніс өнімдері 100 ц кем болмауы міндеттелген және 1 ц көкөніс өндіруге кететін шығындар төменде кестеде келтірілген.
| Көкөніс түрлері | 1 ц көкөніс өндіруге кететін шығындар | |
| Ақша шығыны, мың.теңге | Егіс ауданы, м2 | |
| Көк жуа | ||
| Қияр | ||
| Помидор |
Жалпы өзіндік құн минималды болатын көкөніс өндіру жоспарын анықтаңыз.
2-есеп. Үш фермерлік қожалық 100 мың центнерден кем емес сүт өндіруге тиіс. Әрбір фермерлік қожалық туралы керекті мәлі-меттер төменгі кестеде келтірілген. Жалпы сүттің өзіндік құны минималды болатын өндіріс жоспарын құрыңыз.