Главная | Обратная связь

Тригонометрическая форма комплексного числа

 

α=a+bi

 

Рис.2

 

Определение 1. Число r =|0α|≥0 называется модулем числа α, а угол φ – аргументом α (φ отсчитывается от положительного направления оси R против часовой стрелки).

Аргументов у каждого числа α бесконечно много, их общий вид φ+2πk(kЄZ). У любого комплексного числа, отличного от нуля, существует аргумент. Любое число α≠0 однозначно характеризуется модулем r и каким-либо аргументом φ; эти характеристики обычно называются полярными координатами точки α .

Из рисунка 2 видно, что a=rcos φ, b=rsin φ; тогда α=a+bi=r(cosφ+isinφ).

Определение 2. Форма α=r(cosφ+isinφ) называется тригонометрической формой комплексного числа.

Числа r и φ находят так: , .

Отметим, что если известен tg φ и известно, в какой четверти находится точка α, то однозначно находится угол φ (меньший 2π).

Замечание 1. Аргумент числа α можно отсчитывать и по часовой стрелке, но брать со знаком « - ».

В тригонометрической форме удобно умножать и делить комплексные числа. Нетрудно проверить, используя формулы синуса и косинуса суммы и разности двух углов (см., например, [1]), что справедливы следующие правила: если α=r(cosφ+isinφ) и β=r₁(cosφ₁+isinφ₁), то αβ=rr₁(cos(φ+φ₁)+isin(φ+φ₁)), (5)

и при β¹0

(6)

Из (5) и (6) получаем:

, ,

 

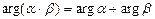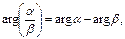, при β¹0.

Замечание 2. Из рис. 1 видно, что |a-b| равен расстоянию между точками α и β (это - геометрический смысл модуля разности). Из этого рисунка, рассмотрев треугольники О(a+b)b и Оab (и некоторые простые частные случаи), получаем

|a|-|b|£|a+b|£|a|+|b|. Геометрическая интерпретация умножения – на рис. 3. Аналогичным образом, заменяя через βa^-1, можно получить геометрическую интерпретацию деления.

Рис.3

Сопряженные числа

Определение. Если a=a+bi,то число =a-bi называется сопряженным с a.

Отметим, что при делении комплексных чисел в алгебраической форме обычно числитель и знаменатель умножаются на число, сопряженное знаменателю (это используется и при доказательстве равенства (6)).