Главная | Обратная связь

Перестановки из n чисел

Пусть М – некоторое конечное множество из n элементов.

Определение. Всякое расположение элементов этого множества в определенном порядке называется перестановкой из n символов.

Например, если 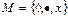, то – перестановка из трех символов.

Элементы множества М можно занумеровать числами 1,2,3,…,n; поэтому вместо перестановок элементов из М можно рассматривать только перестановки чисел {1,2,...,n} (1).

Методом математической индукции легко доказывается

Теорема 1. Число различных перестановок из n чисел равно n!

Доказательство этой теоремы приведено в [1].

Определение 1. Если в некоторой перестановке из n чисел число i стоит раньше j, но i>j, то есть большее число стоит раньше меньшего, то говорят, что пара i,j составляет инверсию.

Например, в перестановке 3,1,4,2 (2) пары 3,1; 4,2 и 3,2 составляют инверсии.

Определение 2. Перестановка называется четной, если общее число инверсий в ней четное; в противном случае перестановка нечетная.

Перестановка (2) нечетная, т.к. в ней всего три инверсии.

Определение 3. Пусть дана некоторая перестановка

…, i,..., j,... (3). Преобразование, при котором числа i и j меняются местами, а остальные остаются на своих местах, называется транспозицией.

После транспозиции чисел i и j в перестановке (3) получим перестановку

…, j,..., i,... (4), где все элементы, кроме i и j,остались на своих местах.

Теорема 2. От любой перестановки из n чисел можно перейти к любой другой перестановке из этих чисел с помощью нескольких транспозиций.

Доказательство. Пусть требуется перейти от перестановки i₁, i₂, ..., i_n (5) к перестановке j₁, j₂, ..., j_n (6). В перестановке (5) производим транспозицию чисел i₁ и j₁; получим j₁, i₂, ..., i₁, ..., i_n (7). В перестановке (7) производим транспозицию чисел i₂ и j₂: j₁, j₂, i₃,..., i_n и т.д. Через конечное число шагов из перестановки (5) получим (6). Теорема доказана.

Теорема 3. Всякая транспозиция меняет четность перестановки.

Доказательство этой теоремы приведено в [1].

Теорема 4. При n≥2 число четных и нечетных перестановок из n чисел одинаково и равно .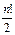

Доказательство. Введем обозначения: Ч – множество всех четных перестановок из n чисел, Н – множество всех нечетных перестановок из этих же чисел. Т.к. n≥2, то среди чисел существуют два различных числа i, j. Во всех перестановках из n чисел проведем транспозицию чисел i и j. Тогда множество Ч перейдет в множество Н₁ и это отображение Ч ® Н₁ – биекция. По теореме 3 Н₁ Ì Н. Значит, число элементов множества Ч и число элементов множества Н связаны неравенством: |Ч|≤|Н| (8). Аналогично, учитывая, что нечетные перестановки при транспозиции чисел i и j перейдут в четные, можно показать, что |Н|≤|Ч| (9). Из неравенств (8) и (9) следует, что |Н|=|Ч|, а тогда из теоремы 1 получаем, что число четных и нечетных перестановок из n чисел равно .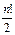

Теорема доказана.