Главная | Обратная связь

Свойства определителей

Определение 1. Если в матрице А строки записать в качестве ее столбцов с теми же номерами, то такое преобразование матрицы называется транспонированием, а полученная матрица называется транспонированной к матрице А и обозначается

.

Аналогично вводится транспонирование определителя d и транспонированный определитель d^’=|A^’|.

 

Свойство 1. При транспонировании определитель не меняется, т.е. |A|=|A^’|. (3)

Доказательство. Пусть d=|A|. Произвольный член (1) определителя d входит в этот определитель со знаком, определяемым подстановкой (2). Рассмотрим транспонированный определитель d^’=|A^’|. Заметим, что все множители произведения (1) входят в разные строки и разные столбцы определителя d^’. Поэтому произведение (1) является и членом определителя d^’. Знак члена (1) в определителе d^’ определяется подстановкой

, (4)

т.к. элемент в d’ находится в строке с номером и столбце с номером .

Очевидно, подстановки (2) и (4) имеют одну и ту же четность (по определению четности подстановки).

Итак, каждый член определителя d является и членом d^’, причем входит в d и d^’ с одним и тем же знаком. Так как и в d, и в d^’ по n! членов, то отсюда следует, что d= d^’.

Свойство доказано.

 

Следствие. В определителе строки и столбцы равноправны (т.е. каждое утверждение, доказанное на языке строк определителя, справедливо и для его столбцов, и обратно).

 

Свойство 2. Если в определителе поменять местами две какие-либо строки, то он изменит только знак.

Доказательство. Рассмотрим произвольный определитель d.

.

Поменяем в нем местами j-ю и k-ю строки. Получим определитель

.

Докажем, что d₁=-d. (5)

Рассмотрим произвольный член определителя d: 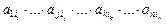(6)

 

Знак члена (6) в d определяется подстановкой (7). Все множители произведения (6) находятся в разных строках и разных столбцах определителя d₁, т.е. (6) является и членом определителя d₁. Знак члена (6) в определителе d₁ определяется подстановкой 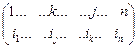(8), т.к. элемент в d₁ находится в j-ой строке и в том же самом 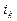-ом столбце, а элемент – в k-ой строке и i_j-ом столбце. Подстановка (8) отличается от (7) только транспозицией чисел j и k в верхней строке, и потому четность подстановки (8) противоположна четности подстановки (7). Следовательно, каждый член определителя d является и членом определителя d₁, но с противоположным знаком. Отсюда, как и выше, получаем: d₁=-d.

 

Свойство 3. Если все элементы какой-либо строки определителя содержат общий множитель, то его можно вынести за знак определителя:

.

Для доказательства достаточно представить первый определитель в виде алгебраической суммы и вынести множитель с.

 

Свойство 4 (достаточные признаки равенства определителя нулю).

Если выполняется хотя бы одно из следующих условий 1)–3), то определитель равен нулю.

1) Определитель содержит строку из нулей.

2) Определитель содержит две одинаковые строки.

3) Определитель содержит две пропорциональные строки.

 

Доказательство.

1) Пусть в определителе содержится нулевая строка. Тогда в каждый член определителя войдет множитель, равный нулю; следовательно, все члены определителя будут равны нулю, и определитель равен нулю.

2) Пусть определитель d содержит две одинаковые строки. Поменяем в нем местами эти строки. Тогда, с одной стороны, определитель не изменится, т.к. эти строки одинаковые. С другой стороны, по свойству 2 он изменит только знак, т.е. станет равным –d. Мы получили, что d=-d; следовательно, т.к. d – комплексное число, то d=0.

3) Пусть определитель содержит две пропорциональные строки.

.

По свойству 3 вынесем общий множитель с за знак определителя; получим определитель с двумя одинаковыми строками. Как показано выше, он равен нулю.

 

Свойство 5 (представление в виде суммы).

.

Для доказательства рассматривается произвольный член определителя и представляется в виде суммы. Подробнее см. в [1].

Замечание 1. С помощью математической индукции это свойство доказывается для любого конечного числа слагаемых.

 

Свойство 6. Если к одной из строк определителя прибавить другую, умноженную на некоторое число, то определитель не изменится.

Доказательство. Рассмотрим определитель

.

Умножим k-ую строку на некоторое число c и прибавим к j-ой строке. Получим

По свойству 5 представим определитель d₁ в виде суммы двух определителей:

 

Первый определитель в этой сумме равен исходному определителю d, а второй содержит две пропорциональные строки и по свойству 4 равен нулю. Свойство доказано.

 

Определение 2. Одна из строк определителя называется линейной комбинацией других, если она представима в виде суммы этих ее строк, умноженных на некоторые числа.

Свойство 7. Если одна из строк определителя является линейной комбинацией остальных строк, то определитель равен нулю.

Для доказательства определитель представляется в виде суммы (по свойству 5) и к слагаемым применяется свойство 4.

Замечание 2. Нетрудно видеть, что все достаточные признаки свойства 4 являются частными случаями признака 7, т.е. (7) – самый общий достаточный признак равенства определителя нулю. В дальнейшем будет доказано, что этот признак является и необходимым.