 |
|
Подстановки n-й степени
Определение 1.Пусть М – конечное множество из n элементов. Всякое биективное преобразование множества М называется подстановкой n-й степени.
Удобно элементы множества М занумеровать натуральными числами (1) и рассматривать подстановки элементов этого множества. Но запись в виде
1→i1,
2→i2,
3→i3,
...
n→in
где  и все ik различны, довольно громоздкая. Поэтому рассмотренную выше подстановку записывают так:
и все ik различны, довольно громоздкая. Поэтому рассмотренную выше подстановку записывают так:  (10) и понимают, что
(10) и понимают, что 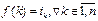 . В нижней строке подстановки f стоит некоторая перестановка из n чисел. Подстановка (10) называется подстановкой стандартного вида.
. В нижней строке подстановки f стоит некоторая перестановка из n чисел. Подстановка (10) называется подстановкой стандартного вида.
Заметим, что из определения подстановки следует, что ее столбцы можно произвольным образом менять местами, т.к. получим то же самое преобразование (т.е. ту же самую подстановку).
Определение 2.Подстановка называется четной, если обе ее строки (перестановки) имеют одинаковые четности, т.е. либо обе четные, либо обе нечетные. В противном случае подстановка называется нечетной.
Докажем, что это определение корректно, т.е. не зависит от формы записи подстановки.
Пусть задана подстановка f. Две ее разные формы записи отличаются только порядком расположения столбцов. В силу теоремы 2 от одного расположения столбцов можно перейти к другому расположению (перестановке) этих же столбцов с помощью нескольких транспозиций столбцов. В силу теоремы 3 при каждой транспозиции столбцов четности верхней и нижней перестановок меняется, однако сохраняется совпадение (несовпадение) четностей строк. По определению четность подстановки при этом не меняется. Этим доказано, что при любой перестановке столбцов подстановки f ее четность одна и та же (т.е. четность подстановки f не зависит от формы ее записи).
Замечание 1. Нетрудно видеть, что четность подстановки можно определить иначе: подстановка называется четной, если общее число инверсий верхней и нижней строк четно, в противном случае подстановка нечетная.
Очевидно, любую подстановку можно записать в стандартном виде (10). При такой записи четность подстановки определяется только четностью ее нижней строки.
Теперь из теоремы 4 получаем
Утверждение. При n≥2 число четных и нечетных подстановок n-ой степени одинаково и равно 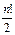 .
.
Подстановки – это преобразования конечного множества, поэтому их можно перемножать по правилам умножения отображений.
¦ : M ® M, g : M ® M,
 ,
,
g¦(i)=g(¦(i))=g(j)=k. Например,
 .
.
Отметим некоторые свойства умножения подстановок. Т.к. подстановки – это биективные отображения, то для них справедливы и доказанные ранее свойства таких отображений:
1. Ассоциативность.
2. Некоммутативность (при n ³3).
3. Существование тождественной подстановки n-ой степени:
 ,
,
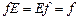 ,где f – любая подстановка n-ой степени.
,где f – любая подстановка n-ой степени.
4. Существование обратной подстановки.
Если подстановка f имеет вид (10), то обратная подстановка f-1 такова:
 , так как
, так как 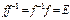 .
.
Замечание 2. Во многих современных книгах подстановки называют перестановками (см., например, [2]).