Главная | Обратная связь

Извлечение корня из комплексного числа

Пусть .

Определение. Число называется корнем n-ой степени из α, если βⁿ=α. (8)

В дальнейшем запись будет означать, что β – один из корней n–ой степени из числа α.

В связи с понятием корня n-ой степени естественно возникают следующие вопросы:

1. Для всякого ли натурального числа n существует хотя бы один комплексный корень n-ой степени из комплексного числа α?

2. Если да, то сколько существует различных комплексных ?

3. Какие они (их вид)?

Постараемся ответить на все эти вопросы.

Дано .

1.Предположим, что в С существует хотя бы один корень

Возьмем один из этих корней 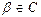. Запишем α и β в алгебраической форме:

α=r(cos φ+isin φ), (9)

β=ρ(cos θ +isin θ), (10)

Так как по нашему предположению βⁿ=α, то, используя формулу Муавра, получаем:

βⁿ=ρⁿ(cos nθ+isin nθ)=α=r(cos φ+isin φ). (11)

В равенстве (11) α двумя способами записано в тригонометрической форме. Ввиду единственности модуля из равенства (11) следует, что ρⁿ=r, т.е. = 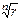(12) (здесь справа стоит арифметический корень).

В равенстве (11) nθ и φ – два аргумента числа α, и поэтому они отличаются на некоторое кратное 2π, т.е. nθ=φ+2k₀ π (для некоторого k₀ Z).

Следовательно, (13)

 

Теперь, подставляя ρ и φ из равенств (12) и (13) в (10), получаем:

(14)

 

 

Мы доказали, что если существует , то он обязан иметь вид (14) при некотором k₀ .
II. Рассмотрим числа вида (14) при любых целых k₀, т.е.

 

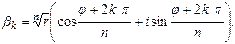(15)

 

(16)

Проверим, является ли β_k корнем 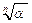. Из равенства (15) и формулы Муавра получаем:

 

=

.

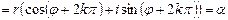т.к. φ +2kp – один из аргументов числа α. Значит, = 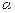, т.е. .

Мы в пункте II доказали, что корни существуют и ими являются все числа вида (15) при произвольных .

 

III. Найдем число различных .

По доказанному в пунктах I и II все различные надо искать среди чисел (15).

1. Покажем, что числа β₀, β₁, … , β_n-1 (17) различны. Предположим противное. Пусть существуют (18), причем (19), но b_l=b_s. (20)

Пусть l >s (21); тогда из равенства (15) имеем: , .

Из условия (20) вытекает, что (22), , т.к. два аргумента одного числа отличаются на некоторое слагаемое, кратное 2π. Следовательно, из (22) получаем: (23). Т.к. , то (24). Это означает, что слева в равенстве (23) стоит правильная дробь, а справа – целое число, т.е. равенство (23) невозможно. Получили противоречие. Отсюда вывод: мы нашли n различных корней (это числа β₀, β₁, … , β_n-1 ).

2. Докажем, что любое число вида (15) совпадает с одним из чисел (17). Для этого используем следующее известное

Утверждение. Любое целое число k можно разделить на некоторое n с неотрицательным остатком r: k=qn+r (25), 0≤r<n.

Число k разделим на n с неотрицательным остатком, получаем: k=qn+r (26), где 0≤r<n (27). Рассмотрим argb_k. Из равенства (15) выписываем: 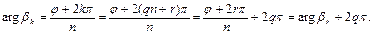(28)

Т.к. в силу (15) , то отсюда и из записи (28) получаем, что в силу неравенства (27). Нами доказано, что числа (17) – все корни .

Все доказанное выше означает справедливость следующей теоремы:

Теорема 1. Пусть α=r(cosφ+isinφ)–любое отличное от нуля комплексное число, n – некоторое натуральное число. Существует ровно n различных комплексных корней n-ой степени из α; все они находятся по формуле и получаются из неё при k=0,1,...,n-1.

Замечание 1. Из полученного в теореме 1 вида корней β_k следует, что все расположены на окружности радиуса . Рассмотрим два «соседних» корня и . Имеем: , . Находим:

=

 

 

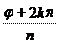
. Следовательно, все делят указанную окружность на n равных частей.

Замечание 2. Т.к. указанная выше окружность пересекает действительную ось только в двух точках, то среди , где , действительных корней может быть не более двух.

Замечание 3. Для корней второй степени из комплексных чисел существует способ их нахождения, связанный с алгебраической формой комплексного числа (см., напр., [1]).