 |
|
Решение квадратных уравнений
Квадратные уравнения с действительными
Коэффициентами
(1), 
, 
.
Корни такого уравнения, как известно, находятся по формулам:
(2), где 
.
Возможны случаи:
А) 
, уравнение имеет два различных действительных корня;
Б) 
, два совпадающих действительных корня;
В) 
, два различных сопряженных комплексных корня, которые находятся по формуле:
.
Квадратные уравнения с комплексными коэффициентами
Рассмотрим уравнение (1) при условии 
, 
. Для решения уравнения так же, как и для уравнений с действительными коэффициентами, можно вывести формулу (2), где дискриминант 
. Учитывая, что квадратных корней из дискриминанта ровно два (по теореме 1) и, очевидно, они отличаются только знаком, получаем
Утверждение. Всякое квадратное уравнение с комплексными коэффициентами имеет два комплексных корня (возможно, совпадающих).
Корни из единицы
Представим единицу в тригонометрической форме: 
(1). Тогда корни n-ой степени из единицы находятся по формулам: 
, причем 
(2) – все различные корни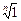 
. Среди корней (2) обязательно есть 1, что позволяет находить их геометрически, т.к. они делят единичную окружность на n равных частей.
Свойства 
- 1=
. - Если n – четное, то
. - Если
, то 
(следует из того, что среди корней 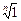есть единица, и они делят единичную окружность на n равных частей). - Если e,d – два корня 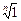, то их произведение равно некоторому корню .
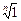Доказательство. По условию 
. Тогда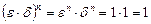 
; значит, 
.
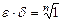- Если , то
. - Если , то для любого целого числа k имеем:
.
Действительно, так как 
, то 
, т.е. 
.
Особая роль 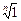видна из следующего утверждения:
Теорема 2. Все корни n-ой степени из комплексного числа α≠0 можно получить умножением какого-то одного 
на все 
.
Доказательство. Пусть 
, 
– все различные корни . Рассмотрим произведения 
(3). Так как 
, то 
; следовательно, 
– один из 
. Все числа (3) – это , их n и, очевидно, они все различны, а так как различных ровно n, то (3) – это все различные (других нет).
Теорема доказана.
Первообразные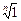
Определение. = 
называется первообразным корнем n-ой степени из 1, если он не является корнем никакой меньшей, чем n, натуральной степени из единицы, т.е. ,но 
, 
.
Теорема 3. Для любого натурального числа n существует хотя бы один первообразный : им является, например, 
(он получается из общего вида корней n-ой степени из 1 
при k=1).
Доказательство. По формуле Муавра имеем: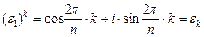 
(4)
Пусть 
; из равенства (4) следует: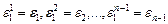 
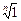. Мы знаем, что – все различные ; т.к. 
, то среди чисел 
единицы нет. Итак, 
, но 
; значит,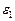 
– первообразный 
. Теорема доказана.
Теорема 4. = является первообразным тогда и только тогда, когда все его степени вида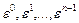 
(5) различны.
Необходимость. Пусть e – первообразный . Докажем, что все числа (5) различны. Предположим, что найдутся такие индексы 
(6), что 
, но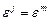 
(7). Пусть 
; тогда из равенства (7) следует: 
(8), причем в силу условия (6) имеем: 
(9). Записи (8) и (9) противоречат тому, что e – первообразный . Следовательно, предположение неверно, и все числа 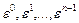различны.
Достаточность. Пусть 
(10) и все числа (5) различны. Тогда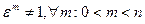 
(11) ибо 
, а остальные из чисел (5) не могут равняться 
. Из равенства (10) и условия (11) следует, что – первообразный (по определению первообразного ).
Теорема доказана.
Следствие. Пусть e –первообразный корень . Тогда числа (5) – все различные . В частности, каждый есть некоторая степень первообразного .
Доказательство. Так как , то по свойствам , числа (5) – это ; в силу теоремы 4 они различны. Их число равно n, и потому числа (5) – это все .
Замечание. Из доказанного следует правило нахождения всех 
:
- Найти один из этих корней
. - Найти первообразный = .
- Составить произведения
. Это – все .
Сформулируем еще один критерий первообразности .
Теорема 5. Число 
, где 
, является первообразным тогда и только тогда, когда числа k и n взаимно простые, т.е. (k,n)=1.
Доказательство этого утверждения можно посмотреть в [1].