 |
|
Вычисление определителей
Определение 1. Пусть d – определитель n-го порядка (с комплексными элементами). Определители порядков 1, 2, …, n, “cодержащиеся” в d, называются минорами определителя d.
Пусть минор М k-го порядка определителя d расположен на пересечениях строк с номерами i1, i2, ..., ik и столбцов с номерами j1, j2, ..., jk этого определителя.
Введем обозначение: SM=( i1+i2+ ...+ik )+( j1+j2+...+jk).
Определение 2. Определитель M’, который получается из определителя d путем вычеркивания всех строк и столбцов, в которых расположен минор М, называется дополнительным минором к минору М в d.
Отметим, что М и М’ – взаимно дополнительные миноры.
Замечание 1. Дополнительный минор есть не у каждого минора: например, у минора n-го порядка нет дополнительного.
Определение 3. Алгебраическим дополнением А минора М определителя d в d называется минор M’, умноженный на  , т.е.
, т.е.  .
.
Обычно используют следующие обозначения: если aij – элемент определителя d, то через Mij обозначает дополнительный минор этого элемента (как минора первого порядка) в определителе d, а Aij – алгебраическое дополнение элемента aij в d, т.е.  .
.
Вычисление определителя n-го порядка можно свести к вычислению одного или нескольких определителей (n-1)-го порядка. Сначала научимся вычислять определители, у которых в одной строке все элементы, кроме одного, отличны от нуля.
Лемма 1.
 (11)
(11)
Доказательство. Если а11=0, то d=0.Пусть а11¹0. Рассмотрим произвольный ненулевой член определителя d. В силу условия леммы из первой строки в него войдет элемент a11. Поэтому все такие члены имеют вид  (12),
(12), 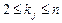 (13),
(13),  . Знак члена (12) в определителе d определяется подстановкой
. Знак члена (12) в определителе d определяется подстановкой  (14). Таким образом, d – алгебраическая сумма членов (12) со знаками, определяемыми подстановкой (14).
(14). Таким образом, d – алгебраическая сумма членов (12) со знаками, определяемыми подстановкой (14).
Если в этой сумме вынести за скобки множитель a11, то получим:  (15), где S – алгебраическая сумма всевозможных членов вида
(15), где S – алгебраическая сумма всевозможных членов вида 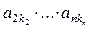 (16) со знаками, определяемыми подстановками (14). Нетрудно видеть, что (16) – это все члены минора M11 . Знак члена (16) в M11 определяется подстановкой
(16) со знаками, определяемыми подстановками (14). Нетрудно видеть, что (16) – это все члены минора M11 . Знак члена (16) в M11 определяется подстановкой  (17) (на самом деле здесь все числа должны быть на единицу меньше, но на четность подстановки это не влияет). Подстановка (17) имеет, очевидно, ту же четность, что и подстановка (14) (т.к. число 1 в нижней строке подстановки (14) не составляет инверсий).
(17) (на самом деле здесь все числа должны быть на единицу меньше, но на четность подстановки это не влияет). Подстановка (17) имеет, очевидно, ту же четность, что и подстановка (14) (т.к. число 1 в нижней строке подстановки (14) не составляет инверсий).
Итак, S – алгебраическая сумма всевозможных членов минора M11 с их знаками, т.е. S=M11. Отсюда из равенства (15) получаем:  (18). Лемма доказана.
(18). Лемма доказана.
Лемма 2.
 (19)
(19)
Доказательство. Для доказательства определитель d с помощью перестановок строк и столбцов преобразуем так, чтобы элемент aij перешел в левый верхний угол, но при этом не изменился дополнительный минор Mij к элементу aij. Для этого i-ую строку определителя d поменяем местами с предыдущей, затем опять с предыдущей и т.д., пока она не займет место первой строки. Заметим, что каждый раз, когда мы меняем местами строки, меняется знак определителя. Получим следующий определитель:
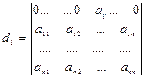 .
.
Очевидно,  (20) и d1 получается из d путем
(20) и d1 получается из d путем
(i-1) перестановок строк. Точно также в определителе d1 c помощью (j-1) перестановок столбцов переводим элемент aij в левый верхний угол.
 и
и  . (21)
. (21)
Подставляя d1 из (20) в (21), получим: 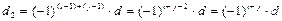 . Следовательно,
. Следовательно,  . (22)
. (22)
В силу леммы 1, примененной к определителю d2, получаем:  (23) (мы использовали то, что в определителе d2 дополнительным минором к элементу aij, будет тот же самый минор, который был дополнительным к aij в d, т.е. Mij ).
(23) (мы использовали то, что в определителе d2 дополнительным минором к элементу aij, будет тот же самый минор, который был дополнительным к aij в d, т.е. Mij ).
Из равенств (22) и (23) следует:  .
.
Лемма доказана.
Теперь мы можем получить правило вычисления любого определителя n-го порядка.
Теорема 5 (разложение определителя по строке). Определитель d равен сумме произведений элементов какой-либо его строки на их алгебраические дополнения в d, т.е.
 (24)
(24)
Доказательство. Рассмотрим в определителе d произвольную i-ую строку. Каждый элемент этой строки представим в виде суммы самого этого элемента и (n-1) нулей следующим образом:
 ,
,
 ,
,
…,

По свойству 5 определитель d тогда можно представить в виде суммы определителей:

Теперь, применяя лемму 2 к каждому из определителей, стоящих справа, и учитывая тот факт, что при нахождении алгебраических дополнений элементов i-ой строки элементы самой этой строки вычеркиваются, т.е. могут быть любыми, мы получим:
 .
.
Теорема доказана.
Некоторые определители (например, содержащие «большие» миноры из нулей) удобнее вычислять с помощью разложения по нескольким строкам, сводящего вычисление определителя n-го порядка к вычислению определителей k-го и (n-k)-го порядков.
Теорема Лапласа. Пусть в определителе n-го порядка d выделены какие-либо k строк (или k столбцов), где 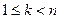 . Тогда сумма произведений всех миноров k-го порядка определителя d, содержащихся в этих строках, на их алгебраические дополнения равна самому определителю d.
. Тогда сумма произведений всех миноров k-го порядка определителя d, содержащихся в этих строках, на их алгебраические дополнения равна самому определителю d.
Доказательство этой теоремы мы не приводим.
Замечание 2. Пусть M1, M2, ..., Ms – все миноры k-го порядка в рассматриваемых строках определителя и, соответственно, А1, А2, ..., Аs – их алгебраические дополнения в d. Тогда теорема утверждает, что
 .
.