Главная | Обратная связь

Еще одно свойство определителей

Теорема 6(фальшивое разложение определителя по строке). Сумма произведений элементов какой-либо строки определителя на алгебраические дополнения соответствующих элементов другой его строки равна нулю.

Доказательство. Пусть дан определитель n-го порядка d. Рассмотрим две его строки:

Докажем, что (25), если . (26)

Заменим элементы j-ой строки произвольными числами с₁, с₂, …, с_n . Получим следующий определитель:

.

Разложим определитель ∆ по его j-ой строке. Учитывая, что остальные строки у определителей d и ∆ одинаковые, а также то, что алгебраические дополнения элементов j-ой строки не зависят от этой строки, мы получим:

(27). Равенство (27) справедливо при любых Полагаем (28), т.е. в определителе ∆ в качестве элементов j-ой строки возьмем снова его i-ую строку. Тогда получим определитель, равный нулю. Подставляя в равенство (27) значения с₁, с₂, …,с_n из (28), получаем равенство (25).

Теорема доказана.

Замечание. Это свойство определителей используется в ряде доказательств (в частности, при установлении вида обратной матрицы).

Глава 5. Матрицы

Простые и двойные суммы

Введем некоторые общематематические понятия.

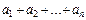Определение 1. Сумма вида называется простой суммой и обозначается , т.е. = . (1)

Здесь i – индекс суммирования, a_i – любые выражения, зависящие от i. Слева в (1) простая сумма записана в свернутом виде, справа – в раскрытом.

Например, .

Свойства простых сумм

1. Простая сумма не зависит от обозначения индекса суммирования, т.е.

. (2)

Для доказательства достаточно раскрыть в (2) обе суммы.

2. Из-под знака простой суммы можно выносить постоянный множитель, т.е. множитель, не зависящий от индекса суммирования:

(3)

Действительно, .

Свойство справедливо для любых слагаемых, для которых справедлив дистрибутивный закон.

 

Двойные суммы

Определение 2.Двойной суммой называют сумму простых сумм следующего вида:

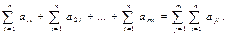(4)

Пример. 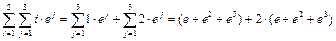.