Главная | Обратная связь

Линейные преобразования неизвестных

Определение 1. Пусть даны две системы неизвестных:

(6) – «старая»,

(7) – «новая».

Переход от системы неизвестных (6) к новой системе (7) называется линейным преобразованием неизвестных, если

,

. . . . . . . . . . . . . . . . . . . . (8)

,

где .

(8) – это линейное преобразование неизвестных (здесь «старые» неизвестные выражаются через «новые»)

 

Заметим, что линейное преобразование (8) удобно записать на языке сумм:

, . (9)

Определение 2. Матрица называется матрицей линейного преобразования (8).

Определение 3. Два линейных преобразования неизвестных называются равными, если равны их матрицы (т.е. если равны соответствующие элементы этих матриц).

Это означает, что если в записи линейного преобразования сменить обозначения неизвестных, то мы получим то же самое линейное преобразование.

 

Введем умножение линейных преобразований неизвестных.

Определение 4. Произведением двух линейных преобразований n известных называют результат их последовательного выполнения.

Рассмотрим линейное преобразование (8) и другое линейное преобразование неизвестных:

,

. . . . . . . . . . . . . . . . . . . . , (10)

,

, – матрицы линейных преобразований (8) и (10).

Пусть требуется перемножить линейные преобразования (8) и (10). Для нахождения их произведения надо неизвестные из (10) подставить в равенства (8). Нетрудно видеть, что получим новое линейное преобразование неизвестных:

,

. . . . . . . . . . . . . . . . . . . . , (11)

с матрицей .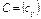

Найдем выражение элементов матрицы С через элементы матриц А и В. Для этого равенство (10) запишем в виде:

(10’), .

Подставим y_j из (10’) в (9). Используя свойства простых и двойных сумм, получаем:

(12) Сравнивая записи (11) и (12), видим: , 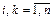. (13)

Мы получили, что матрица С произведения линейных преобразований с матрицами А и В находится по формулам (13).

Определение 5. Матрицу произведения двух линейных преобразований назовем произведением матриц этих преобразований.

По этому определению умножение матриц проводится по формулам (13).

Расписывая сумму (13), имеем:

. (14)

Это означает, что элемент с_ik матрицы С равен произведению i-ой строки матрицы А на k-й столбец матрицы В.

Умножение матриц

Во множестве М_n всех матриц n-го порядка с комплексными элементами по формуле (13) мы ввели операцию умножения.

Отметим некоторые ее свойства.

1. Умножение матриц n-го порядка при n³2 некоммутативно, т.е. при n≥2 найдутся две матрицы А и В, такие, что . Например,

, но .

2. Умножение матриц ассоциативно: .

Доказательство можно посмотреть в [1].

3. Среди матриц n-го порядка существует такая, которая играет роль единицы:

.

Она обладает свойством: .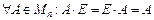

Заметим, что единичная матрица – это матрица тождественного линейного преобразования, при котором просто переобозначаются неизвестные:

.

Обратная матрица

Возникает вопрос: существует ли для данной матрицы 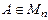такая матрица А^-1, чтобы

? (16)

Для решения этого вопроса рассмотрим следующее утверждение.

Теорема (об определителе произведения матриц). Если , то определитель произведения этих матриц равен произведению определителей сомножителей, т.е.

. (17)

Доказательство этой теоремы можно найти в [1].

Следствие 1. Определитель произведения конечного числа матриц равен произведению определителей сомножителей, т.е. .

Доказательство данного утверждения проводится методом математической индукции.

 

Определение. Если определитель матрицы А равен нулю, то матрица называется вырожденной, в противном случае – невырожденной.

 

Следствие 2. Если А и В – две невырожденные матрицы, то произведение АВ – также невырожденная матрица.

Очевидно, что если , то в силу теоремы .

Следствие 3. Если хотя бы одна из матриц-сомножителей вырожденная, то и их произведение будет вырожденной матрицей.

Доказательство очевидно.

Следствие 4. Вырожденные матрицы не имеют обратных.

Доказательство. Пусть . Предположим, что существует обратная матрица А^-1 к матрице А, т.е. . Тогда по следствию 3 матрица Е – вырожденная, т.к. А – вырожденная; но . Полученное противоречие доказывает следствие 4.

Следствие 5. Если у матрицы А есть обратная, то A – невырожденная матрица.

 

Пусть теперь А – произвольная невырожденная матрица n-го порядка.

.

Рассмотрим определитель d матрицы А и для каждого элемента a_ij найдем его алгебраическое дополнение A_ij. Из этих алгебраических дополнений составим следующую матрицу:

.

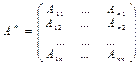В ней j-й столбец представляет собой набор алгебраических дополнений j-ой строки определителя d в естественном порядке.

Матрица А* называется присоединенной к матрице А.

Найдем произведение матриц А и А*.

. (1)

Заметим, что мы использовали правило разложения определителя по строке и фальшивое разложения определителя по строке.

Из равенства (1) видно, что если d≠0, т.е. матрица А невырожденная, то разделив все элементы матрицы А* на d, получим матрицу А^-1:

, (2)

.

Отметим, что из этого равенства следует: |A|×|A^-1|=|E|=1, то есть |A^-1|= .

Доказано

Утверждение 1. У каждой невырожденной матрицы существует хотя бы одна (невырожденная) обратная матрица вида (2).