 |
|
Алгебраическая операция
Дано некоторое множество М.
Определение. Будем говорить, что во множестве М определена алгебраическая операция, если указан закон, по которому любой паре элементов a и b из этого множества, взятых в определенном порядке, ставится в соответствие единственный элемент с из этого же множества М.
Заметим, что этим мы определяем только однозначные операции.
Условие, что результат операции 
называется замкнутостью операции.
Чаще всего алгебраическую операцию называют либо умножением (ab=c), либо сложением (a+b=c).
Примеры.В произвольном непустом множестве М можно ввести операции:
1. 
;
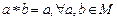2. пусть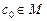 
, тогда 
.
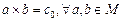Группы
Группы – множества с одной алгебраической операцией (чаще всего ее называют умножением). Поэтому мы приводим сначала определение группы по умножению.
Определение 1. Множество G, в котором определена операция умножения, называется группой (относительно этой операции), если выполняются следующие требования (аксиомы группы):
1. Ассоциативность: 
.
2. Существование единичного элемента: 
.
3. Существование обратного элемента: 
.
Замечание. Точно также, как для матриц, можно доказать единственность единичного и обратного элементов в группе.
Примеры групп по умножению:
1. Самая маленькая группа может состоит из одного элемента – единицы.
2. Множество из двух элементов 
.
3. Множество корней n-ой степени из единицы 
(при фиксированном 
). Действительно, из свойств корней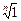 
следует, что если 
,то 
, т.е. операция умножения замкнута. Существование единичного и обратного элементов в Cn очевидно.
4. Множество действительных чисел без нуля.
5. Множество Sn подстановок n-ой степени – симметричная группа n-ой степени. При n≥2 эта группа некоммутативная.
Определение 2.Множество G, в котором определена операция сложения, называется группой (относительно этой операции), если выполняются следующие условия:
1. Ассоциативность: 
.
2. Существование нулевого элемента:
.
3. Существование противоположного элемента:
.
Примеры групп по сложению:
1. Число 0.
2. Z – множество целых чисел.
3. Четные числа Z2.
4. Множество комплексных чисел.
5. Mn(R) – множество всех матриц n-го порядка с элементами из R.
В этом множестве следующим образом определено сложение матриц: если 
и 
, то 
. Нетрудно проверить, что Mn(R) – группа по сложению; ее нулевой элемент имеет вид
, а противоположный элемент 
.
6. Ф – множество всех функций действительной переменной с одной и той же областью определения. Роль нуля играет функция, все значения которой равны нулю: f(x)≡0; функция -f(x) – противоположная f(x).
Кольца
Кольца – это множества с двумя алгебраическими операциями – сложением и умножением.
Определение 1. Множество К, в котором определены две алгебраические операции – сложение и умножение, называется кольцом, если
1. К – группа по сложению.
2. Сложение коммутативно: 
.
3. Умножение ассоциативно: 
.
4. Выполняются два дистрибутивных закона: 
.
Заметим, что дистрибутивные законы – единственные аксиомы, связывающие сложение и умножение.
Примеры колец:
1. К={0}.
2. Множество целых чисел Z.
3. Множество четных чисел Z2.
4. Множество комплексных чисел.
5. Mn(R) – множество всех матриц n-го порядка с элементами из R.
6. Ф – множество всех функций действительной переменной, определенных на R.
Замечание 1. В книге [1] в определении кольца требуется и коммутативность умножения. Это – более частный вид колец. Обычно такая коммутативность не требуется.